Kako izračunati područje romba?

U ovom ćete članku naučiti kako pronaći područje romba raznim metodama. Zahvaljujući ovim formulama, lako će se riješiti problemima geometrije, jer će ovdje članak opisati kako izračunati područje romba, znajući veličinu dijagonale većeg i donjeg, bočnog i promjera upisanog kruga u rombu.

Područje romba možete saznati po različitim formulama. Dovoljno je znati svojstva ove figure i svojstva drugih figura, jer se rombus može podijeliti u trokute, može se izjednačiti s paralelogramom itd. Ispod ćete vidjeti takve formule. Također morate znati kako se rombus i paralelogram razlikuju. Prema matematičkoj definiciji. Rombus je lik takvog paralelograma s jednakim stranama, ali za razliku od kvadrata - rombus nema ravne kutove. Ali zbroj dvaju kutova u podnožju romba bit će 180 stupnjeva. Sve će to znanje dobro doći za izračunavanje područja romba, a zatim detaljnije.

Kako izračunati područje romba - svojstva slike

Prije izračuna područja romba, bolje je upoznati se sa svojstvima ove figure. Doista, zahvaljujući znanju ovih karakteristika, lakše će dokazati vjerojatnost određene formule. Ranije je već spomenuto što je rombus. To je brojka jednaka svim stranama jednakim suprotnim oštrim i glupim uglovima, ali nije ravna.

Romb ima sljedeća svojstva:

• sve su strane jednake jedna drugoj
• kutovi koji leže jedan nasuprot su također jednaki
• dijagonali ove brojke su bisektori, na točki sjecišta podijeljeni su u jednake segmente
• diagonali se također presijecaju u sredini romba i pod pravim kutom
• suprotne strane figura ne mogu se presijecati, čak i ako proširite zrake, one su paralelne, poput paralelograma.

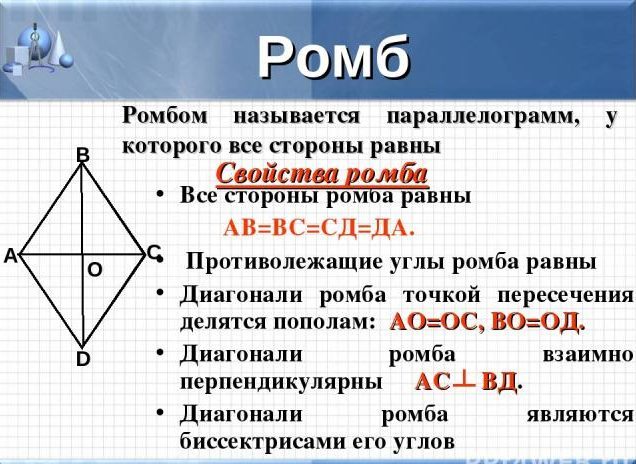
VAŽNO: Imajte na umu da se rombus može podijeliti u četiri pravokutna trokuta, koji će biti jednaki u području, ili za dva jednakostranična identična trokuta, pogledajte gornju sliku.

Kako izračunati područje romba?

Dakle, saznajmo kako se izračunava područje romba. Iskoristimo formulu za područje pravokutnika, gdje:

• S \u003d a • bgdje su A, B su strane pravokutnika.

Tako da je jasno kako ukloniti formulu područja romba iz ove formule, vidi obrazloženje:

1. Nacrtajte rombus, napravite visinu do baze BH romba.
2. Od točke D do linije oglasa, također nacrtajte visinu CH1.
3. Ispada da su trokut ABH i trokut CH1D jednaki jedni drugima na dvije uobičajene strane, ∠ u poklopcu između njih.
4. Dakle, ah \u003d dh1. Površina rezultirajućeg kvadrata bit će jednaka području romba
5. Dakle, BH • HH1 - Ovo je područje romba, drugim riječima, djelo BH romba na stranu AD -a i bit će područje romba, budući da je HH1 \u003d BC, a BH je the visina.

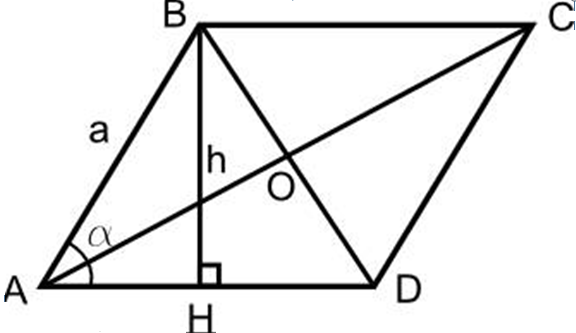
To proizlazi iz dokaza da:

• S rombus \u003d a • h i mjereno u kvadratnim jedinicama.

Kako pronaći područje romba, znajući kut i stranu geometrijske figure?

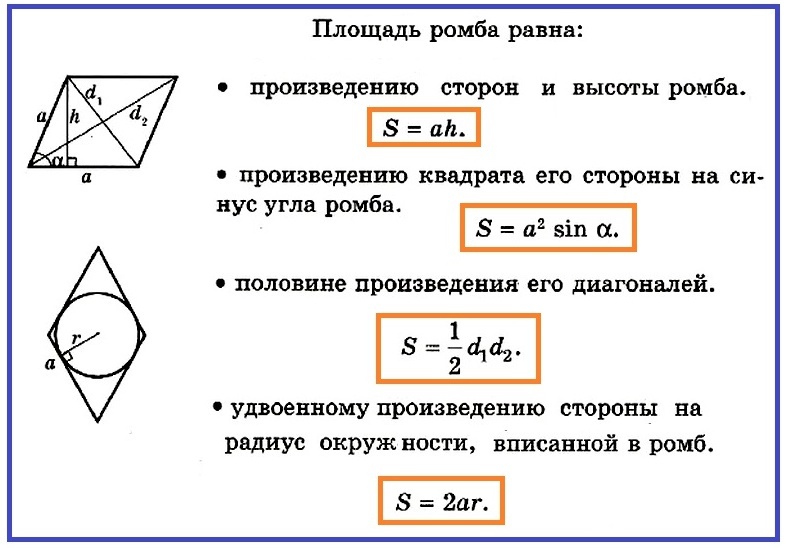
Sada znamo kako izgleda formula područja romba, možemo pronaći područje Rhomba na istoj formuli, znajući koja je strana romba jednaka bočnoj strani romba, na primjer, oštra u bazi, kao u Fotografija ispod.

• S \u003d a • h

Ali u našem slučaju, mi smo nepoznati visinu romba, to treba pronaći. Da biste to učinili, morat ćete razmotriti pravokutni trokut, koji se ispostavilo kada je visina povučena u bazu romba.

U ovom je trokutu poznat hipotenuza i ∠α. Da biste izračunali područje cijele figure, morat ćete pronaći visinu. ALI h \u003d a • grijeh oni. Dakle, područje jednakostraničnog paralelograma (rombus) je:

• S \u003d a • a • grijeh oni ax \u003d a² • sinown.

Kako izračunati područje romba, znajući njegove dijagonale?

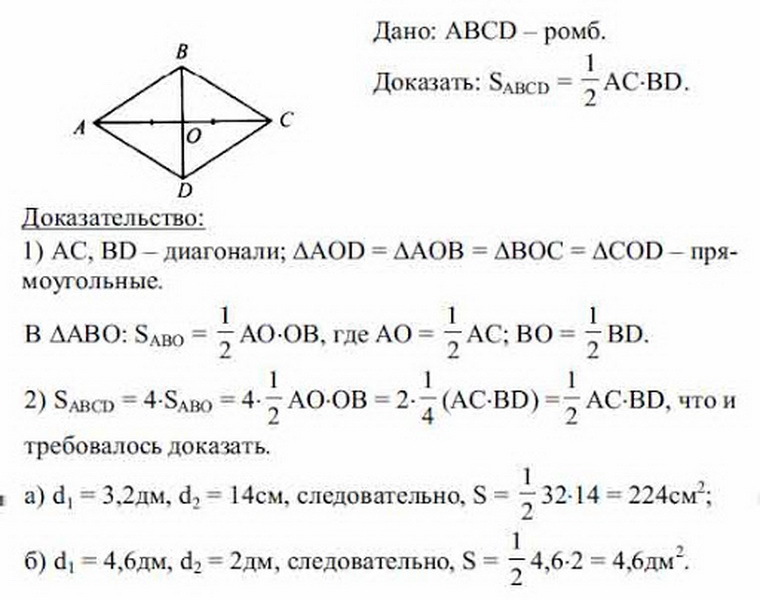
Da biste saznali formulu područja romba, kada su poznati samo (a, b) dijagonali, treba uzeti u obzir sljedeći primjer. BCDA se daje - rombus i znaju što su dijagonali jednaki. Sada je potrebno pronaći područje jednakostraničnog paralelograma u smislu dijagonala.

Prije toga već su razmatrana svojstva romba. Dijagonali romba su jednaki, na mjestu sjecišta podijeljeni su u jednake segmente. Iz toga proizlazi da su svi trokuti koji su upisani na sliku kao rezultat sjecišta oba dijagonala jednak jedni drugima i pravokutni su (s tri strane). Da biste pronašli područje romba, dovoljno je pronaći područje jednog trokuta i pomnožiti podatke dobivene za 4.

Ukupno, ispada da:

• S Rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Ukupni kvadratni s Romm bit će \u003d rad a • b (dijagonali) podijeljen s dva: S \u003d 1/2 a • b

Kako izračunati područje romba, znajući njegovu stranu i polumjer kruga upisane u njemu?

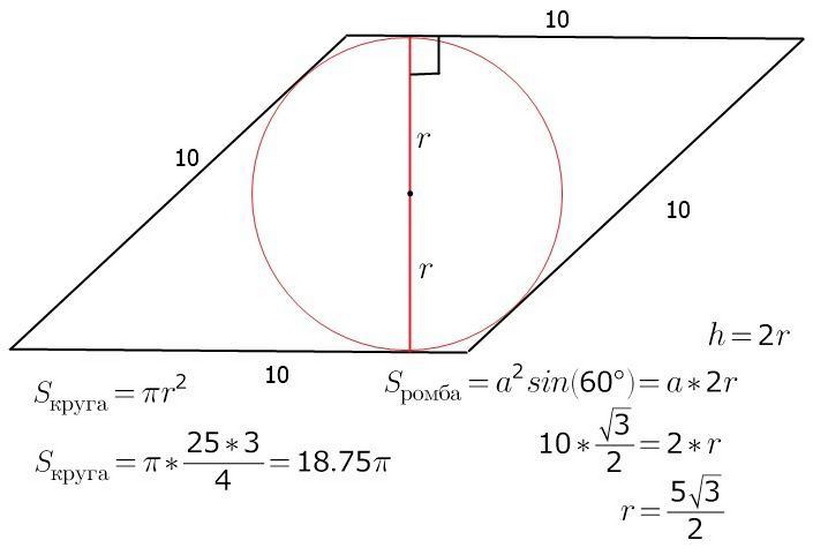
Područje romba može se izračunati znanjem R - polumjera i A - duljinom strane figure. Već je poznato da će S - područje figure biti jednako djelo b - bočna na H - visini. Kroz središte kruga, to će biti i središte sjecišta a, B je dijagonali romba. Izvršite visinu i istodobno promjer romba. Slika pokazuje da su visina slike dva polumjera kruga. Sada će biti lako pronaći područje samog romba:

• S \u003d a • h \u003d a • 2r

U nastavku pogledajte primjer zadatka na ovu temu.

I dalje vidite takve članke o ovoj temi ovdje:

1. Područje pravokutnika, kako pronaći?
2. Kako pronaći područje kruga?
3. Kvadratna površina - formule.

Video: Primjer kako izračunati područje romba