Kako pronaći kvadratno područje ako je obod poznat, dijagonalno? Kako pronaći kvadrat kvadrata upisanog u krug i opisan u blizini opsega: formula, primjeri rješavanja problema. Kako pronaći bočnu i dijagonalu kvadrata, ako je poznato njegovo područje?

Pročitajte članak kako biste znali kako pronaći područje kvadrata na različite načine.

Kvadrat je jednakostranični pravokutnik. Ovaj pravi i ravni četverokut ima jednakost na svim stranama, uglovima i dijagonalima. Zbog činjenice da postoji takva jednakost, formula za izračunavanje područja i drugih karakteristika malo je modificirana u usporedbi s drugim matematičkim figurama. Ali to ne čini zadatke previše kompliciranim. Analizirajmo sve formule i rješenja ovog članka.

Kako pronaći stranu trga, znajući njegovo područje?

Kvadrat S. Izravni i kvadratni kvadrati izračunavaju se formulom: a Pomnožiti sa b.. Ali budući da kvadrat ima potpunu jednakost stranaka, njezino će područje biti jednako: S \u003d (a) U drugom stupnju.  Kako saznati veličinu bočne strane trga, znajući njegovo područje?

• Ako je poznato područje kvadratnog kvadrata, tada pronalazimo stranu izračunavanjem područja ispod kvadratnog korijena.
• Na primjer, površina kvadrata je 49, čija je strana jednaka?
• 49 \u003d (a) U drugom stupnju. Riješenje: a \u003d korijen od 49 \u003d 7. Odgovor: 7.

Ako trebate pronaći stranu kvadratnog kvadrata, čija je površina predugo, a zatim upotrijebite kalkulator. Prvo nazovite broj područja, a zatim pritisnite korijenski znak na tipkovnici kalkulatora. Rezultirajući broj bit će odgovor.

Kako pronaći kvadratnu dijagonalu ako je poznato njegovo područje?

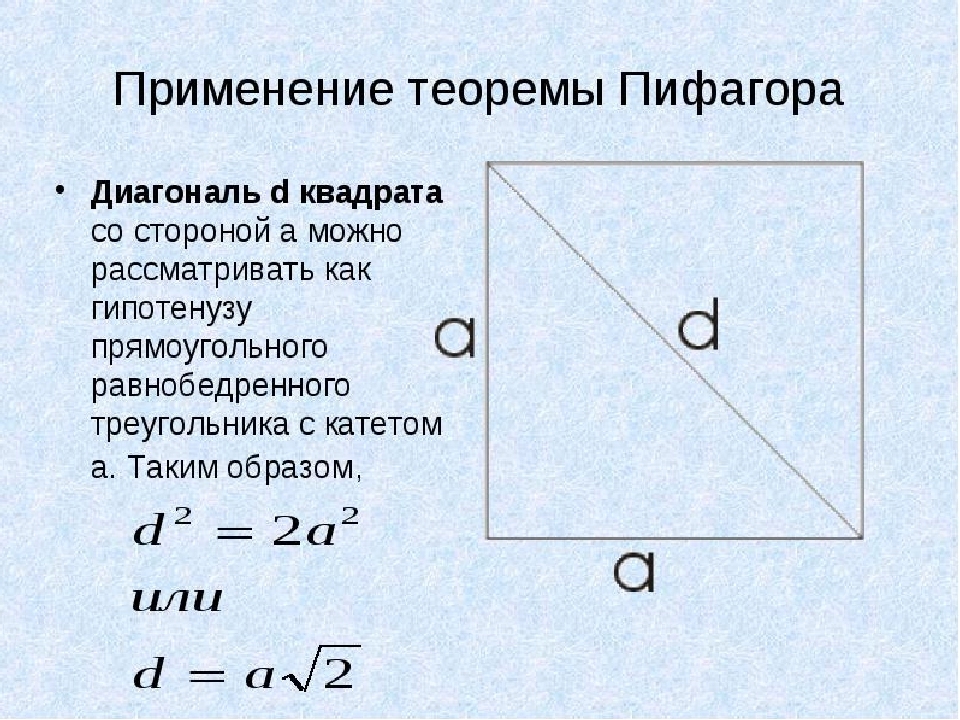
U ovom ćemo primjeru upotrijebiti teorem Pithagoras. U kvadratu su sve strane jednake, a dijagonalni d. Razmotrit ćemo kao hipotenuzu pravokutnog trokuta Isosceles s nogom a. Sada pronalazimo kvadratnu dijagonalu ako je poznato njegovo područje:

• Da ne bismo slikali čitavu pitagorejsku teoremu, odlučit ćemo o drugoj opciji: d \u003d aising, gdje je a strana kvadrata.
• Dakle, znamo da je područje kvadrata, na primjer, jednako 64. Dakle, jedna strana a \u003d √64 \u003d 8.
• Ispada D \u003d 8√2. Korijen 2 ne ispadne cijeli broj, tako da u odgovoru možete napisati na ovaj način: d \u003d 8√2. Ali, ako želite izračunati vrijednost, koristite kalkulator: √2 \u003d 1.41421356237 i pomnožite s 8, ispada 11, 3137084.

Važno: U matematici obično u odgovoru nisu ostali brojevi s velikim brojem brojeva. Potrebno je zaokružiti ili otići s korijenom. Stoga je odgovor na dijagonalu ako je područje 64 kako slijedi: d \u003d 8√2.

Kako pronaći kvadratno područje kroz dijagonalu?

Formula za pronalaženje kvadratnog područja kroz dijagonalu je jednostavna:

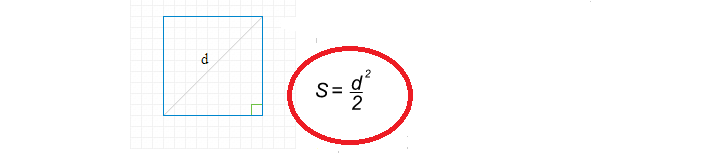
Sada napišimo rješenje za pronalaženje kvadratnog područja kroz dijagonalu:

• Dijagonalni d \u003d 8.
• 8 na trgu je 64.
• 64 Podijelite s 2 jednaka 32.
• Područje kvadrata je 32.

Savjet: Ovaj zadatak ima još jedno rješenje kroz teorem Pitagore, ali je složeniji. Stoga koristite rješenje koje smo ispitali.

Kako pronaći kvadratno područje, znajući njegov obod?

Perimetar kvadratnog trga P. P. - Ovo je zbroj svih strana. Da biste pronašli njegovo područje, znajući svoj obod, prvo morate izračunati stranu kvadrata. Riješenje:

• Pretpostavimo da je perimetar 24. Podijelite 24 na 4 strane, ispada da je 6 - ovo je jedna strana.
• Sada koristimo formulu za pronalaženje područja, znajući koja je strana kvadratnog kvadrata jednaka: S \u003d a u kvadratu, s \u003d 6 u kvadratu \u003d 36.
• Odgovor: 36

Kao što vidite, znajući perimetar trga, samo pronađite njegovo područje.

Kako pronaći područje kvadrata napisanog u krug s danim polumjerom?

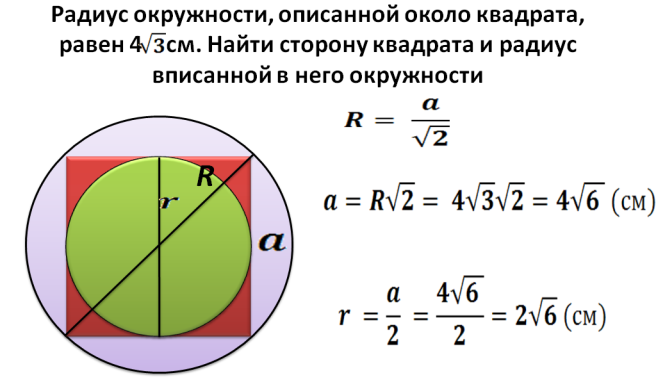
Radius R - Ovo je pola dijagonale kvadrata napisanog u krug. Sada možemo pronaći dijagonalu po formuli: d \u003d 2*r. Zatim nalazimo kvadrat kvadrata upisanog u krug s danim polumjerom:

• Dijagonala je 2 umnožavanja s polumjerom. Na primjer, polumjer je 5, tada je dijagonala jednaka 2*5=10.
• Opisano je gore kako pronaći kvadrat kvadrata ako je dijagonala poznata: S \u003d dijagonala u kvadratu podijeljena na 2. S \u003d 10*10 i podijelite s 2 \u003d 50.
• Odgovor - 50.

Ovaj je zadatak malo složeniji, ali također lako riješen ako znate sve formule.

Kako pronaći područje kvadrata opisanog u blizini kruga s danim polumjerom?

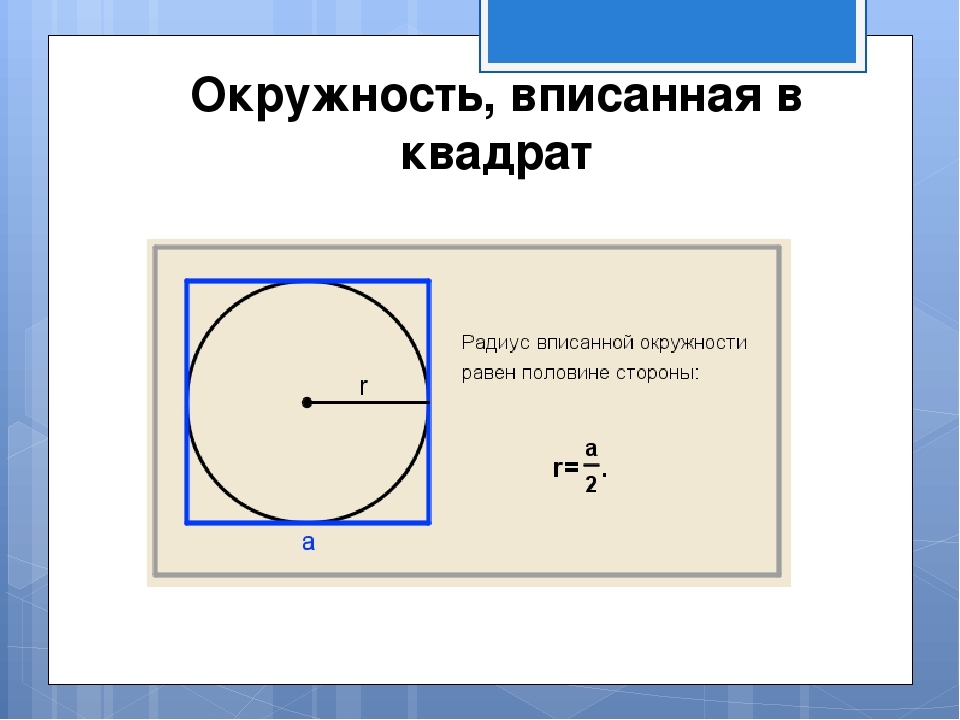
Slika pokazuje da je polumjer upisanog kruga jednak polovici bočne strane. Strana se nalazi prema obrnutoj formuli koja je prikazana na slici: a \u003d 2*r. Tada pronalazimo područje kvadrata opisanog u blizini kruga s danim polumjerom prema formuli S \u003d i u kvadratu. Riješenje:

• Pretpostavimo da je polumjer 7. Strana kvadrata A je 2*7 \u003d 14.
• S \u003d 14 u kvadratu \u003d 196.

Ako razumijete suštinu rješavanja takvih problema, tada ih možete brzo i jednostavno riješiti. Pogledajmo još nekoliko primjera.

Primjeri rješavanja problema na temu "Square Square"

Da biste popravili pokriveni materijal i zapamtili sve formule, potrebno je riješiti nekoliko primjera problema na temu "kvadratne površine". Započinjemo s jednostavnim zadatkom i prelazimo na rješavanje složenijih:

Sada znate kako koristiti formulu za kvadrat trga, što znači da možete obaviti bilo koji zadatak. Uspjeh u budućem treningu!

Video: Izračunavanje kvadratnog područja