วิธีการคำนวณพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูน?

ในบทความนี้คุณจะได้เรียนรู้วิธีการค้นหาพื้นที่ของ Rhombus ด้วยวิธีการต่าง ๆ ต้องขอบคุณสูตรเหล่านี้มันจะได้รับการแก้ไขอย่างง่ายดายโดยปัญหาเรขาคณิตเพราะที่นี่บทความจะอธิบายวิธีการคำนวณพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนโดยรู้ขนาดของเส้นทแยงมุมของขนาดใหญ่และล่างด้านข้างและเส้นผ่านศูนย์กลางของวงกลมที่จารึกไว้ ในรูปสี่เหลี่ยมขนมเปียกปูน

คุณสามารถค้นหาพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนโดยสูตรที่แตกต่างกัน มันเพียงพอที่จะทราบคุณสมบัติของตัวเลขและคุณสมบัติของตัวเลขอื่น ๆ เนื่องจากรูปสี่เหลี่ยมขนมเปียกปูนสามารถแบ่งออกเป็นสามเหลี่ยมได้มันสามารถบรรจุด้วยรูปสี่เหลี่ยมด้านขนาน ฯลฯ ด้านล่างคุณจะเห็นสูตรดังกล่าว คุณต้องรู้ว่ารูปสี่เหลี่ยมขนมเปียกปูนและรูปสี่เหลี่ยมด้านขนานแตกต่างกันอย่างไร ตามคำจำกัดความทางคณิตศาสตร์ รูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปของรูปสี่เหลี่ยมด้านขนานที่มีด้านที่เท่ากัน แต่แตกต่างจากสี่เหลี่ยม - รูปสี่เหลี่ยมขนมเปียกปูนไม่มีมุมตรง แต่ผลรวมของสองมุมที่ฐานของโรมจะอยู่ที่ 180 องศา ความรู้ทั้งหมดนี้จะมีประโยชน์สำหรับการคำนวณพื้นที่ของ Rhombus จากนั้นในรายละเอียดเพิ่มเติม

วิธีการคำนวณพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูน - คุณสมบัติของรูป

ก่อนที่จะคำนวณพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนจะเป็นการดีกว่าที่จะทำความคุ้นเคยกับคุณสมบัติของตัวเลขนี้ อันที่จริงด้วยความรู้เกี่ยวกับลักษณะเหล่านี้มันจะง่ายกว่าที่จะพิสูจน์ความน่าจะเป็นของสูตรเฉพาะ ก่อนหน้านี้มันถูกกล่าวถึงแล้วว่ารูปสี่เหลี่ยมขนมเปียกปูนคืออะไร มันเป็นรูปที่มีเท่ากับทุกด้านเท่ากับมุมที่คมชัดและเป็นใบ้ แต่ไม่ตรง

Rhombus มีคุณสมบัติดังต่อไปนี้:

• ทุกด้านมีความเท่าเทียมกัน
• มุมที่อยู่ตรงข้ามกันก็เท่ากัน
• เส้นทแยงมุมของรูปนี้เป็น bisectors ที่จุดสี่แยกแบ่งออกเป็นส่วนที่เท่ากัน
• เส้นทแยงมุมยังตัดกันในศูนย์กลางของรูปสี่เหลี่ยมขนมเปียกปูนและที่มุมขวา
• ด้านตรงข้ามของตัวเลขไม่สามารถตัดกันได้แม้ว่าคุณจะขยายรังสีพวกมันก็ขนานกันเหมือนสี่เหลี่ยมด้านขนาน

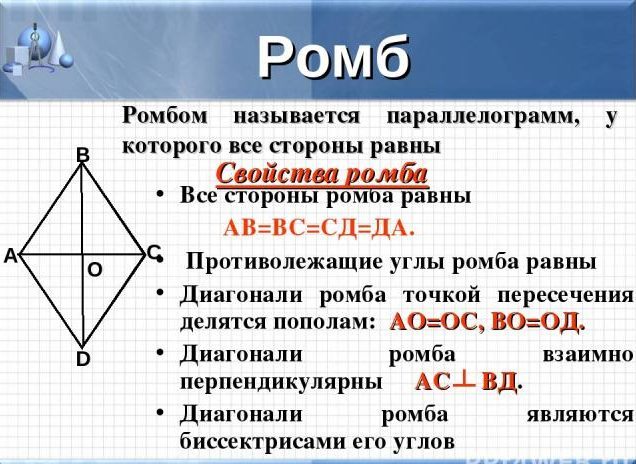
สำคัญ: โปรดทราบว่ารูปสี่เหลี่ยมขนมเปียกปูนสามารถแบ่งออกเป็นสามเหลี่ยมสี่เหลี่ยมสี่เหลี่ยมซึ่งจะเท่ากันในพื้นที่หรือสองสามเหลี่ยมที่เหมือนกันสองเท่าดูภาพด้านบน

วิธีการคำนวณพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูน?

ดังนั้นเรามาดูกันว่าการคำนวณพื้นที่ซักซ้อมเป็นอย่างไร มาใช้ประโยชน์จากสูตรสำหรับพื้นที่ของสี่เหลี่ยมที่:

• S \u003d A • Bโดยที่ a, b คือด้านข้างของสี่เหลี่ยมผืนผ้า

เพื่อให้ชัดเจนว่าจะลบสูตรของพื้นที่ของโรมออกจากสูตรนี้ได้อย่างไรดู คำอธิบาย:

1. วาดรูปสี่เหลี่ยมขนมเปียกปูนให้สูงถึงฐานของ Rhombus BH
2. จากจุด D ไปยังบรรทัดโฆษณายังดึงความสูงของ CH1
3. ปรากฎว่าสามเหลี่ยม ABH และสามเหลี่ยม CH1D มีค่าเท่ากับสองด้านทั่วไป∠ในฝาครอบระหว่างพวกเขา
4. ดังนั้น AH \u003d DH1 พื้นที่ของสี่เหลี่ยมที่เกิดขึ้นจะเท่ากับพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูน
5. ดังนั้น BH • HH1 - นี่คือพื้นที่ของ Rhombus ในคำอื่น ๆ ความสูง.

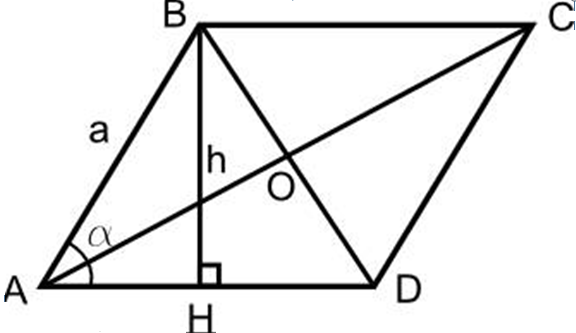
มันตามมาจากหลักฐานว่า:

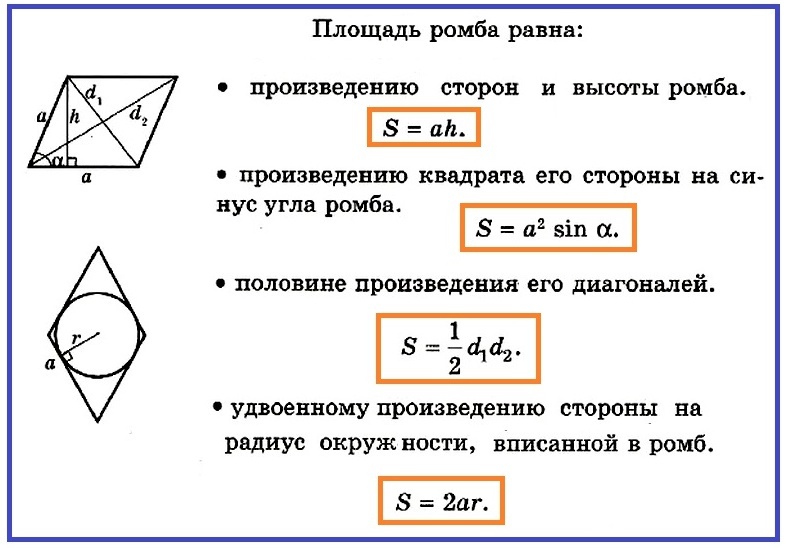
• s rhombus \u003d a • h และวัดในหน่วยสี่เหลี่ยม

จะหาพื้นที่ของโรมบัสได้อย่างไรรู้มุมและด้านข้างของรูปเรขาคณิต?

ตอนนี้เรารู้แล้วว่าสูตรของพื้นที่โรมบัสเป็นอย่างไรเราสามารถหาพื้นที่สี่เหลี่ยมโรมในสูตรเดียวกันรู้ว่าด้านข้างของรูปสี่เหลี่ยมขนมเปียกปูนเท่ากับด้านข้างของโรมเช่นนั้นคมชัดที่ฐานเช่นเดียวกับ ภาพด้านล่าง

• s \u003d a • h

แต่ในกรณีของเราเราไม่รู้จักความสูงของรูปสี่เหลี่ยมขนมเปียกปูนมันควรจะพบ ในการทำเช่นนี้คุณจะต้องพิจารณารูปสามเหลี่ยมสี่เหลี่ยมซึ่งกลับกลายเป็นว่าเมื่อความสูงถูกดึงไปที่ฐานของรูปสี่เหลี่ยมขนมเปียกปูน

ในสามเหลี่ยมนี้เป็นที่รู้จัก hypotenuse และ∠α ในการคำนวณพื้นที่ของตัวเลขทั้งหมดคุณจะต้องค้นหาความสูง และ h \u003d a •บาปพวกเขา ดังนั้นพื้นที่ของรูปสี่เหลี่ยมด้านขนาน (รูปสี่เหลี่ยมขนมเปียกปูน) คือ:

• s \u003d a • a •บาปพวกเขาขวาน \u003d a²• sinown

วิธีการคำนวณพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนรู้ว่าเส้นทแยงมุมของมัน?

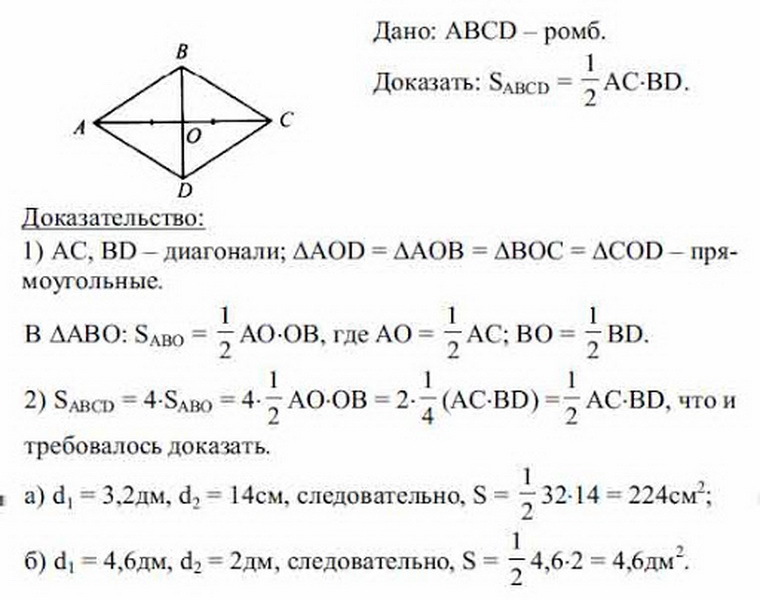
ในการค้นหาสูตรของพื้นที่ของ Rhombus เมื่อทราบว่าเป็นเส้นทแยงมุม (a, b) เท่านั้นตัวอย่างต่อไปนี้ควรได้รับการพิจารณา BCDA ได้รับ - รูปสี่เหลี่ยมขนมเปียกปูนและรู้ว่าเส้นทแยงมุมเท่ากัน ตอนนี้มีความจำเป็นต้องค้นหาพื้นที่ S ของสี่เหลี่ยมด้านขนานดุลยภาพในแง่ของเส้นทแยงมุม

ก่อนหน้านี้คุณสมบัติของรูปสี่เหลี่ยมขนมเปียกปูนได้รับการพิจารณาแล้ว เส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูนมีค่าเท่ากันที่จุดตัดพวกเขาจะแบ่งออกเป็นส่วนที่เท่ากัน จากนี้มันเป็นไปได้ว่ารูปสามเหลี่ยมทั้งหมดที่ถูกจารึกไว้ในรูปอันเป็นผลมาจากการตัดกันของเส้นทแยงมุมทั้งสองนั้นเท่ากันและเป็นรูปสี่เหลี่ยมผืนผ้า (ทั้งสามด้าน) ในการค้นหาพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนมันก็เพียงพอที่จะหาพื้นที่ของสามเหลี่ยมหนึ่งและคูณข้อมูลที่ได้รับ 4

โดยรวมปรากฎว่า:

• s rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, AC, Total Square S romm จะเป็น \u003d Work A • B (diagonals) หารด้วยสอง: S \u003d 1/2 A • B

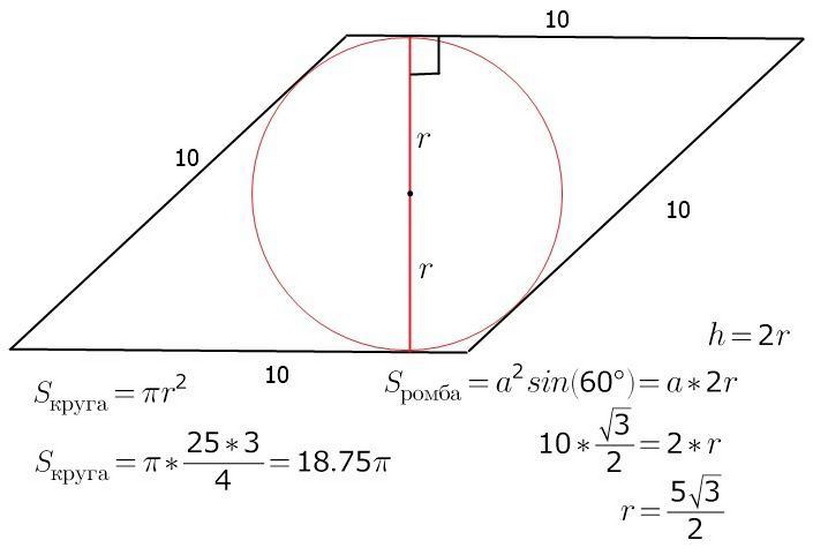
วิธีการคำนวณพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนรู้ด้านข้างและรัศมีของวงกลมที่จารึกไว้ในนั้น?

พื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนสามารถคำนวณได้โดยการรู้รัศมี r - และความยาวของด้านข้างของรูป เป็นที่ทราบกันดีว่า S - พื้นที่ของตัวเลขจะเท่ากับงาน B - ด้านบนความสูง H - ผ่านศูนย์กลางของวงกลมมันจะเป็นศูนย์แยก A, B คือเส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูน ดำเนินการความสูงและในเวลาเดียวกันเส้นผ่านศูนย์กลางของรูปสี่เหลี่ยมขนมเปียกปูน ภาพแสดงให้เห็นว่าความสูงของรูปเป็นสองรัศมีของวงกลม ตอนนี้มันจะง่ายที่จะหาพื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูน:

• s \u003d a • h \u003d a • 2r

ด้านล่างดูตัวอย่างของงานในหัวข้อนี้

ยังคงเห็นบทความดังกล่าวในหัวข้อนี้ที่นี่:

1. พื้นที่ของสี่เหลี่ยมผืนผ้าหาได้อย่างไร?
2. จะหาพื้นที่วงกลมได้อย่างไร?
3. พื้นที่สี่เหลี่ยม - สูตร.

วิดีโอ: ตัวอย่างของวิธีการคำนวณพื้นที่ของ rhombus