จะหาพื้นที่สี่เหลี่ยมจัตุรัสได้อย่างไรหากเป็นที่รู้จักกันในแนวทแยงหรือไม่? วิธีการค้นหาสี่เหลี่ยมจัตุรัสจัตุรัสที่จารึกไว้ในวงกลมและอธิบายใกล้เส้นรอบวง: สูตรตัวอย่างของปัญหาการแก้ปัญหา จะหาด้านข้างและเส้นทแยงมุมของสี่เหลี่ยมได้อย่างไรหากเป็นที่รู้จักกันในพื้นที่?

อ่านบทความเพื่อทราบวิธีการค้นหาพื้นที่สี่เหลี่ยมในรูปแบบที่แตกต่างกัน

เนื้อหา

สี่เหลี่ยมเป็นสี่เหลี่ยมผืนผ้าดุล จัตุรัสที่เหมาะสมและแบนนี้มีความเท่าเทียมกันในทุกด้านมุมและเส้นทแยงมุม เนื่องจากความจริงที่ว่ามีความเท่าเทียมกันเช่นนี้สูตรสำหรับการคำนวณพื้นที่และลักษณะอื่น ๆ จะถูกปรับเปลี่ยนเล็กน้อยเมื่อเทียบกับตัวเลขทางคณิตศาสตร์อื่น ๆ แต่สิ่งนี้ไม่ได้ทำให้งานซับซ้อนเกินไป มาวิเคราะห์สูตรและวิธีแก้ปัญหาทั้งหมดสำหรับบทความนี้

จะหาด้านข้างของจัตุรัสได้อย่างไรรู้ว่าพื้นที่ของมัน?

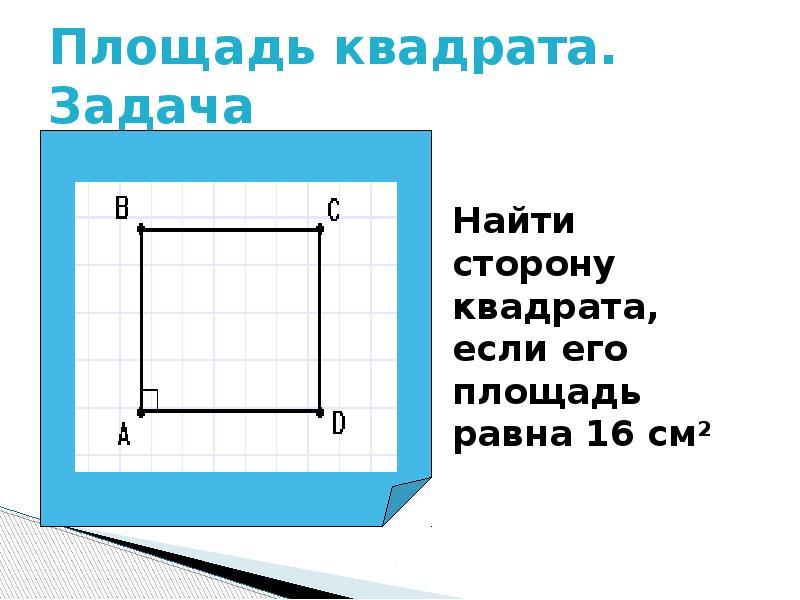
สี่เหลี่ยม พ. สี่เหลี่ยมตรงและสี่เหลี่ยมจัตุรัสคำนวณโดยสูตร: อัน คูณด้วย พ.ส.. แต่เนื่องจากจัตุรัสมีความเท่าเทียมกันอย่างสมบูรณ์ของคู่กรณีพื้นที่ของมันจะเท่ากัน: s \u003d (a) ในระดับที่สอง.จะหาขนาดของด้านข้างของจัตุรัสได้อย่างไรรู้ว่าพื้นที่ของมัน?

หากพื้นที่ของสี่เหลี่ยมสี่เหลี่ยมเป็นที่รู้จักเราจะพบด้านข้างโดยการคำนวณพื้นที่จากใต้รากสแควร์
ตัวอย่างเช่นพื้นที่ของสี่เหลี่ยมคือ 49 แล้วด้านข้างเท่าไหร่?
49 \u003d (a) ในระดับที่สอง. วิธีการแก้: a \u003d รูทของ 49 \u003d 7 คำตอบ: 7.

หากคุณต้องการค้นหาด้านข้างของสแควร์สแควร์พื้นที่ที่ยาวเกินไปให้ใช้เครื่องคิดเลข ก่อนหมุนหมายเลขของพื้นที่แล้วกดเครื่องหมายรูทบนแป้นพิมพ์เครื่องคิดเลข หมายเลขผลลัพธ์จะเป็นคำตอบ

จะหาเส้นทแยงมุมสี่เหลี่ยมได้อย่างไรหากเป็นที่รู้จักกันในพื้นที่?

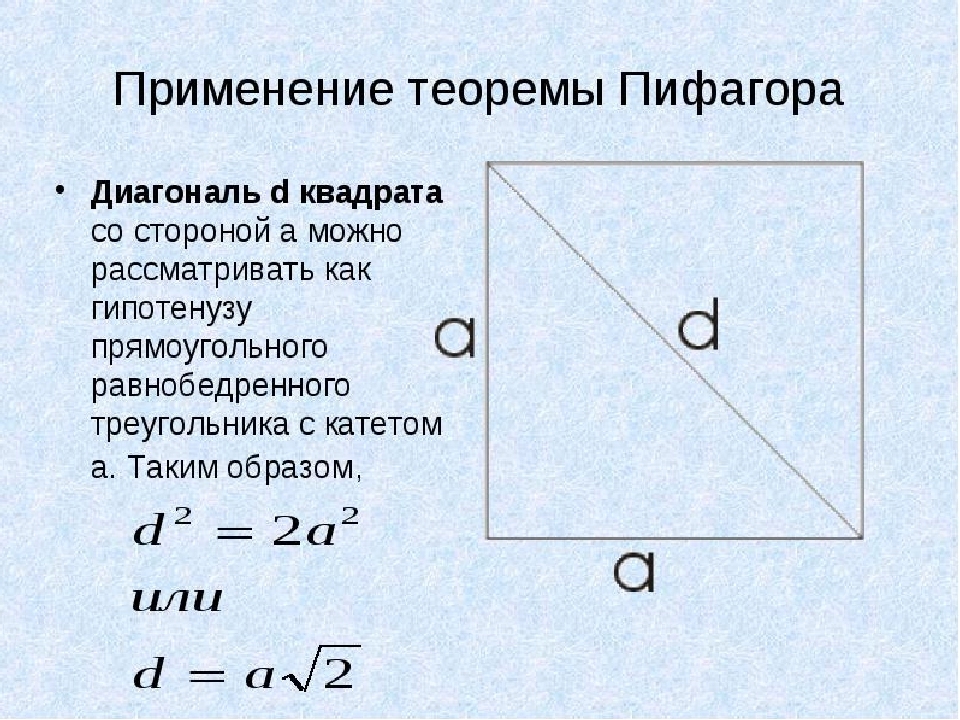
ในตัวอย่างนี้เราจะใช้ทฤษฎีบท Pythagoras ในสี่เหลี่ยมจัตุรัสทุกด้านมีค่าเท่ากันและเส้นทแยงมุม ค. เราจะพิจารณาว่าเป็นภาพสามเหลี่ยมที่มีรูปสี่เหลี่ยมจัตุรัสสามเหลี่ยมที่มีขา อัน. ตอนนี้เราพบเส้นทแยงมุมสี่เหลี่ยมถ้าพื้นที่เป็นที่รู้จัก:

เพื่อไม่ให้ทาสีทฤษฎีบทพีทาโกรัสทั้งหมดเราจะตัดสินใจเลือกตัวเลือกที่สอง: d \u003d aising โดยที่ A คือด้านข้างของสี่เหลี่ยมจัตุรัส
ดังนั้นเราจึงรู้พื้นที่ของสแควร์ตัวอย่างเช่นมันเท่ากับ 64 ดังนั้นด้านหนึ่ง a \u003d √64 \u003d 8
ปรากฎ d \u003d 8√2. รูทของ 2 ไม่เปิดหมายเลขทั้งหมดดังนั้นในคำตอบที่คุณสามารถเขียนด้วยวิธีนี้: d \u003d 8√2. แต่ถ้าคุณต้องการคำนวณค่าให้ใช้เครื่องคิดเลข: √2 \u003d 1.41421356237 และคูณด้วย 8 มันกลับกลายเป็น 11, 3137084.

สำคัญ: โดยทั่วไปแล้วในวิชาคณิตศาสตร์จะไม่มีตัวเลขที่มีตัวเลขจำนวนมากอยู่ในการตอบสนอง มีความจำเป็นที่จะต้องปัดเศษหรือออกไปด้วยราก ดังนั้นคำตอบของเส้นทแยงมุมคือถ้าพื้นที่เป็น 64 ดังนี้: d \u003d 8√2.

จะหาพื้นที่สี่เหลี่ยมผ่านแนวทแยงได้อย่างไร?

สูตรสำหรับการค้นหาพื้นที่สี่เหลี่ยมจัตุรัสผ่านแนวทแยงนั้นง่าย:

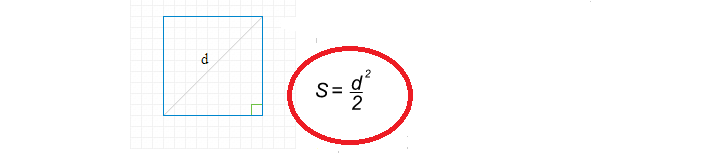
ตอนนี้เรามาเขียนวิธีแก้ปัญหาเพื่อค้นหาพื้นที่สี่เหลี่ยมจัตุรัสผ่านเส้นทแยงมุม:

เส้นทแยงมุม d \u003d 8
8 ในจัตุรัสคือ 64
64 หารด้วย 2 เท่ากับ 32
พื้นที่สี่เหลี่ยมคือ 32

คำแนะนำ: งานนี้มีวิธีแก้ปัญหาอื่นผ่านทฤษฎีบท Pythagoras แต่มันซับซ้อนกว่า ดังนั้นใช้วิธีแก้ปัญหาที่เราตรวจสอบ

จะหาพื้นที่สี่เหลี่ยมได้อย่างไรรู้ถึงปริมณฑล?

ปริมณฑลของสแควร์สแควร์ น. - นี่คือผลรวมของทุกฝ่าย ในการค้นหาพื้นที่ของมันเมื่อรู้ปริมณฑลคุณต้องคำนวณด้านข้างของสี่เหลี่ยมจัตุรัสก่อน วิธีการแก้:

สมมติว่าปริมณฑลคือ 24 แบ่ง 24 ด้านออกเป็น 4 ด้านปรากฎว่า 6 - นี่คือด้านหนึ่ง
ตอนนี้เราใช้สูตรในการค้นหาพื้นที่รู้ว่าด้านข้างของสี่เหลี่ยมจัตุรัสเท่ากันเท่ากับ: S \u003d A ในสี่เหลี่ยมจัตุรัส S \u003d 6 ในตาราง \u003d 36.
ตอบ: 36

อย่างที่คุณเห็นรู้ถึงปริมณฑลของจัตุรัสเพียงแค่หาพื้นที่ของมัน

จะหาพื้นที่ของสี่เหลี่ยมจตุรัสที่จารึกไว้เป็นวงกลมที่มีรัศมีที่กำหนดได้อย่างไร?

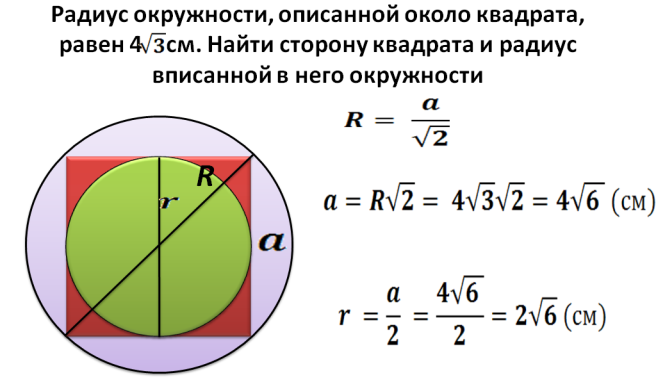
รัศมี R - นี่คือครึ่งเส้นทแยงมุมของสแควร์ที่จารึกไว้ในวงกลม ตอนนี้เราสามารถหาแนวทแยงได้ด้วยสูตร: d \u003d 2*r. ต่อไปเราจะพบสี่เหลี่ยมจัตุรัสของสี่เหลี่ยมจตุรัสที่จารึกไว้ในวงกลมที่มีรัศมีที่กำหนด:

เส้นทแยงมุมคือ 2 คูณด้วยรัศมี ตัวอย่างเช่นรัศมีคือ 5 จากนั้นเส้นทแยงมุมจะเท่ากัน 2*5=10.
มันอธิบายไว้ข้างต้นวิธีการค้นหาสี่เหลี่ยมจัตุรัสถ้าเป็นที่รู้จักในแนวทแยง: s \u003d เส้นทแยงมุมในสี่เหลี่ยมแบ่งออกเป็น 2 s \u003d 10*10 และหารด้วย 2 \u003d 50
ตอบ - 50.

งานนี้ซับซ้อนกว่าเล็กน้อย แต่ก็แก้ไขได้ง่ายหากคุณรู้จักสูตรทั้งหมด

จะหาพื้นที่ของสี่เหลี่ยมที่อธิบายไว้ใกล้วงกลมที่มีรัศมีที่กำหนดได้อย่างไร?

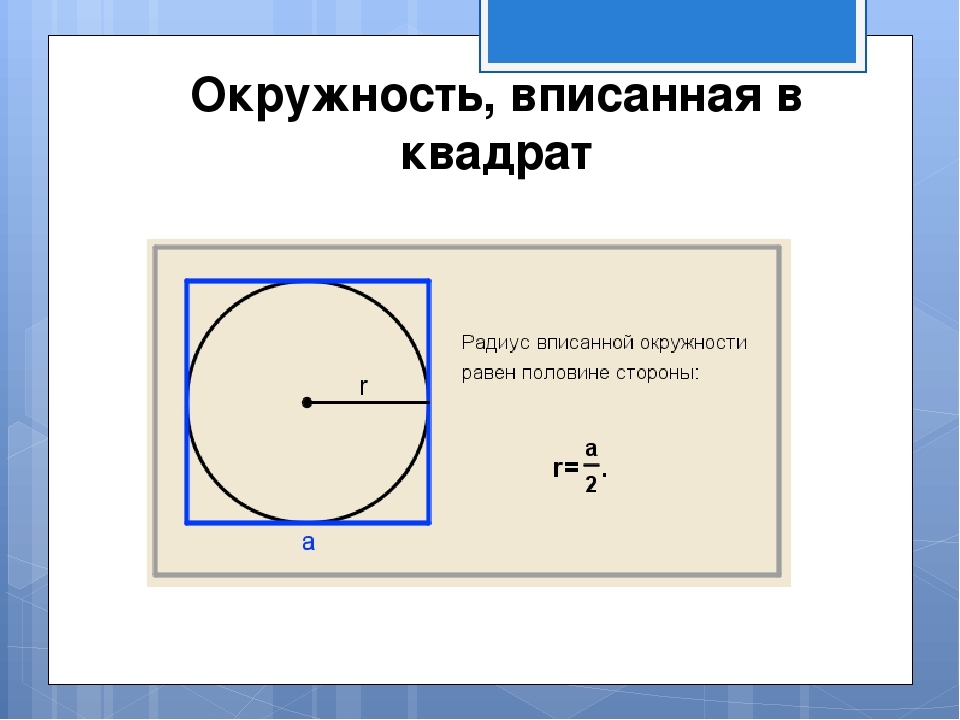
ภาพแสดงให้เห็นว่ารัศมีของวงกลมที่จารึกอยู่เท่ากับครึ่งหนึ่งของด้านข้าง ด้านข้างตั้งอยู่ตามสูตรย้อนกลับที่ปรากฎในภาพ: a \u003d 2*r. จากนั้นเราจะพบพื้นที่ของสี่เหลี่ยมที่อธิบายไว้ใกล้วงกลมที่มีรัศมีที่กำหนดตามสูตร s \u003d และในสี่เหลี่ยมจัตุรัส. วิธีการแก้:

สมมติว่ารัศมีคือ 7 ด้านข้างของสี่เหลี่ยม A คือ 2*7 \u003d 14
s \u003d 14 ในตาราง \u003d 196.

หากคุณเข้าใจสาระสำคัญของการแก้ปัญหาดังกล่าวคุณสามารถแก้ปัญหาได้อย่างรวดเร็วและง่ายดาย ลองดูตัวอย่างอีกสองสามตัวอย่าง

ตัวอย่างของการแก้ปัญหาในหัวข้อ "สแควร์สแควร์"

ในการแก้ไขวัสดุที่ครอบคลุมและจดจำสูตรทั้งหมดจำเป็นต้องแก้ปัญหาปัญหาหลายประการเกี่ยวกับธีมของ "พื้นที่สี่เหลี่ยมจัตุรัส" เราเริ่มต้นด้วยงานง่าย ๆ และย้ายไปแก้ปัญหาที่ซับซ้อนมากขึ้น: