Ako vypočítať oblasť kosoštvorca?

V tomto článku sa dozviete, ako nájsť oblasť kostra s rôznymi metódami. Vďaka týmto vzorcom sa ľahko vyrieši problémami s geometriou, pretože tu článok opíše, ako vypočítať plochu kosoštvorca, pri v kostore.

Oblasť Rhombusu nájdete rôznymi vzorcami. Stačí poznať vlastnosti tohto obrázku a vlastnosti iných čísel, pretože kosoštvorca sa dá rozdeliť na trojuholníky, môže sa porovnávať s rovnobežníkom atď. Nižšie uvidíte takéto vzorce. Musíte tiež vedieť, ako sa Rhombus a rovnobežník líšia. Podľa matematickej definície. Rhombus je postava takého rovnobežníka s rovnakými stranami, ale na rozdiel od štvorca - rhombus nemá priame uhly. Ale súčet dvoch uhlov na spodnej časti kostra bude 180 stupňov. Všetky tieto znalosti sa hodia na výpočet oblasti kosoštvorca, potom podrobnejšie.

Ako vypočítať plochu kostra - vlastnosti obrázku

Pred výpočtom oblasti kostra je lepšie oboznámiť sa s vlastnosťami tohto obrázku. Vďaka znalosti týchto charakteristík bude ľahšie dokázať pravdepodobnosť konkrétneho vzorca. Skôr sa už spomínalo, čo je Rhombus. Je to postava, ktorá sa rovná všetkým stranám rovnajúcim sa opačným ostrým a hlúpym rohom, ale nie rovná.

Rhombus má nasledujúce vlastnosti:

• všetky strany sa navzájom rovnajú
• rohy ležiace oproti sebe sú tiež rovnaké
• diagonály tohto obrázku sú bisektory, v bode križovatky sú rozdelené do rovnakých segmentov
• diagonály sa tiež pretínajú do stredu kosoštvorca a v pravých uhloch
• opačné strany čísel sa nemôžu pretínať, aj keď roztiahnete lúče, sú rovnobežné ako rovnobežník.

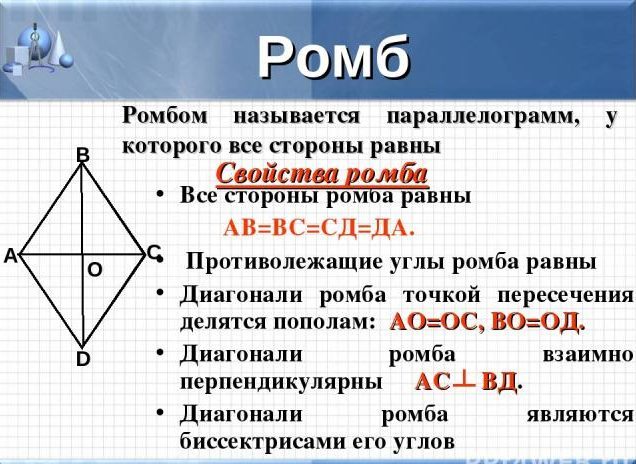
Dôležité: Vezmite prosím na vedomie, že kosoštvorca sa dá rozdeliť do štyroch pravouhlých trojuholníkov, ktoré budú rovnaké v oblasti, alebo dvoma rovnostrannými rovnakými trojuholníkmi, pozri obrázok vyššie.

Ako vypočítať oblasť kosoštvorca?

Poďme teda zistiť, ako sa vypočítava oblasť Rhombus. Využite výhody vzorca pre oblasť obdĺžnika, kde:

• S \u003d A • Bkde a, b sú strany obdĺžnika.

Takže je zrejmé, ako odstrániť vzorec oblasti kostra z tohto vzorca, pozri vysvetlenie:

1. Nakreslite kostru, urobte výšku na spodok BH Rhombus.
2. Z bodu D do reklamnej čiary tiež nakreslite výšku CH1.
3. Ukazuje sa, že trojuholník ABH a trojuholník CH1D sú navzájom rovnaké na dvoch spoločných stranách, ∠ v kryte medzi nimi.
4. Takže ah \u003d dh1. Oblasť výsledného štvorca sa bude rovnať oblasti kosoštvorca
5. Takže bh • hh1 - Toto je oblasť kosoštvorca, inými slovami, dielo bh rhombusu na bok Ad a bude oblasť Rhombus, pretože hh1 \u003d bc a bh je výška.

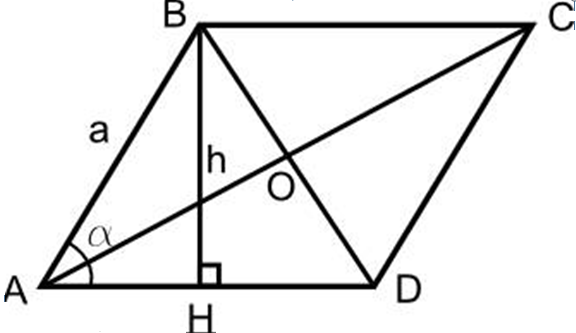
Vyplýva to z dôkazu, že:

• S Rhombus \u003d A • H a merané v štvorcových jednotkách.

Ako nájsť oblasť kosoštvorca, poznať roh a stranu geometrickej postavy?

Teraz vieme, ako vyzerá vzorec oblasti Rhombus, môžeme nájsť oblasť Rhomba na rovnakom receptúre, pretože vieme, čo sa strana kosoštvorca rovná boku kostra, napríklad ostrý na základni, ako v Fotografia nižšie.

• S \u003d a • h

Ale v našom prípade nie sme neznáme výšku kosoštvorca, malo by sa to nájsť. Aby ste to dosiahli, budete musieť zvážiť obdĺžnikový trojuholník, ktorý sa ukázal, keď bola výška vtiahnutá k spodnej časti kostra.

V tomto trojuholníku je známy hypotenus a ∠α. Na výpočet plochy celej postavy budete musieť nájsť výšku. A h \u003d a • hriech. Takže oblasť rovnostranného rovnobežníka (kosoštvorca) je:

• S \u003d a • a • hriech, Ax \u003d a² • Sinown.

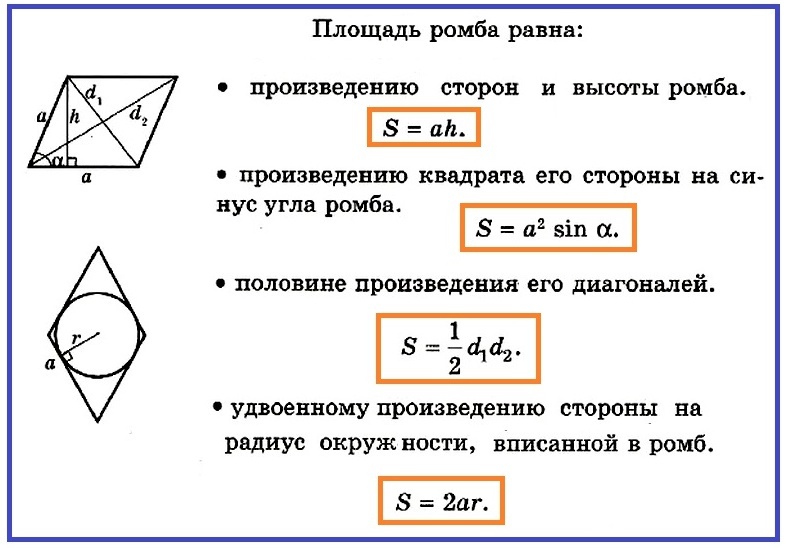
Ako vypočítať oblasť kosoštvorca, poznáte jej uhlopriečky?

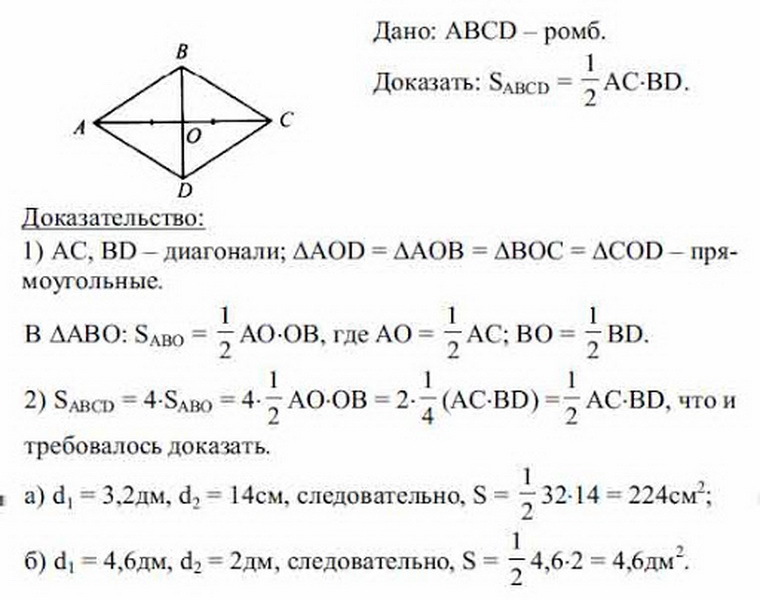
Na zistenie vzorca oblasti kosoštvorca, keď sú známe iba (a, b) diagonály, mal by sa zvážiť nasledujúci príklad. BCDA je uvedený - Rhombus a viem, čo sú uhlopriečky rovnaké. Teraz je potrebné nájsť plochu rovnostranného rovnobežníka z hľadiska diagonálov.

Predtým sa už zvážili vlastnosti Rhombusu. Diagonály kostra sú rovnaké, v bode križovatky sú rozdelené do rovnakých segmentov. Z toho vyplýva, že všetky trojuholníky, ktoré sú napísané na obrázku v dôsledku priesečníka oboch diagonalov, sa tiež navzájom rovnajú a sú obdĺžnikové (na troch stranách). Na nájdenie oblasti kosoštvorca stačí nájsť plochu jedného trojuholníka a vynásobiť údaje získané 4.

Celkovo sa ukázalo, že:

• S Rhombus \u003d 4 (1/2 AO • OB + 1/2 Bo • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Celkový štvorcový Romm bude \u003d práca a • B (diagonály) vydelené dvoma: S \u003d 1/2 A • B

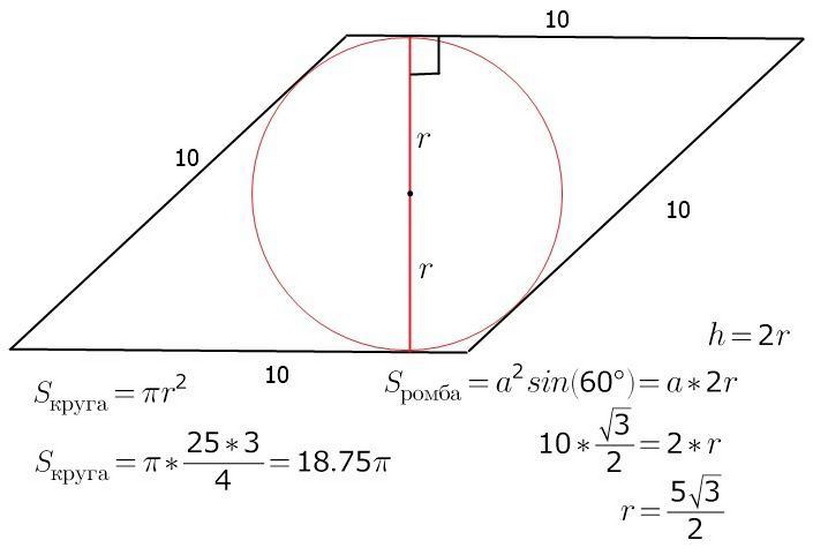
Ako vypočítať plochu kostra, poznáte jej stranu a polomer kruhu, ktorý je v nej uvedený?

Oblasť kosoštvorca sa dá vypočítať poznaním polomeru R - polomeru a - dĺžky strany obrázku. Je už známe, že S - plocha obrázku sa bude rovnať práci B - strana na výške H -. Cez stred kruhu to bude tiež križovatka A, B je diagonála kostra. Vykonajte výšku a zároveň priemer kostra. Obrázok ukazuje, že výška obrázku je dva polomery kruhu. Teraz bude ľahké nájsť oblasť samotného kostra:

• S \u003d a • h \u003d a • 2r

Nižšie nájdete príklad úlohy na túto tému.

Stále si pozrite tieto články o tejto téme tu:

1. Oblasť obdĺžnika, ako nájsť?
2. Ako nájsť oblasť kruhu?
3. Štvorcová oblasť - vzorce.

VIDEO: Príklad toho, ako vypočítať plochu kostra