Ako nájsť štvorcovú plochu, ak je obvod známy, diagonálny? Ako nájsť štvorec štvorca vpísaného v kruhu a opísané blízko obvodu: vzorec, príklady riešenia problémov. Ako nájsť stranu a diagonál štvorca, ak je jeho oblasť známa?

Prečítajte si článok, aby ste vedeli, ako nájsť štvorcovú oblasť rôznymi spôsobmi.

Spokojnosť

Štvorec je rovnostranný obdĺžnik. Tento správny a plochý štvorec má rovnosť vo všetkých stranách, rohoch a diagonáloch. Vzhľadom na to, že existuje taká rovnosť, vzorec na výpočet oblasti a ďalšie charakteristiky je v porovnaní s inými matematickými číslami mierne upravený. To však nie je príliš komplikované. Analyzme všetky vzorce a riešenia tohto článku.

Ako nájsť stranu námestia, poznať jeho oblasť?

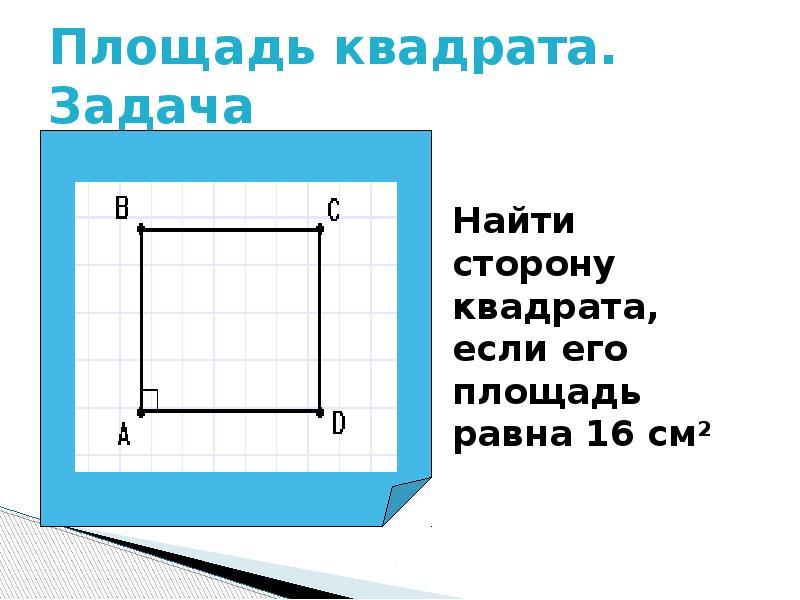
Námestie S. Priame a štvorcové štvorce sa počítajú podľa vzorca: a Vynásobiť b.. Ale keďže štvorec má úplnú rovnosť strán, jej oblasť bude rovnaká: S \u003d (a) v druhom stupni.Ako zistiť veľkosť strany štvorca, poznáte jej oblasť?

Ak je známa plocha štvorcového štvorca, potom nájdeme stranu vypočítaním plochy pod štvorcovým koreňom.
Napríklad oblasť štvorca je 49, potom, čo je strana rovná?
49 \u003d (a) v druhom stupni. Riešenie: a \u003d koreň 49 \u003d 7. Odpoveď: 7.

Ak potrebujete nájsť stranu štvorcového štvorca, ktorej plocha je príliš dlhá, použite kalkulačku. Najprv vytočte číslo oblasti a potom stlačte koreňovú značku na klávesnici kalkulačky. Výsledné číslo bude odpoveďou.

Ako nájsť štvorcový diagonálny, ak je jeho oblasť známa?

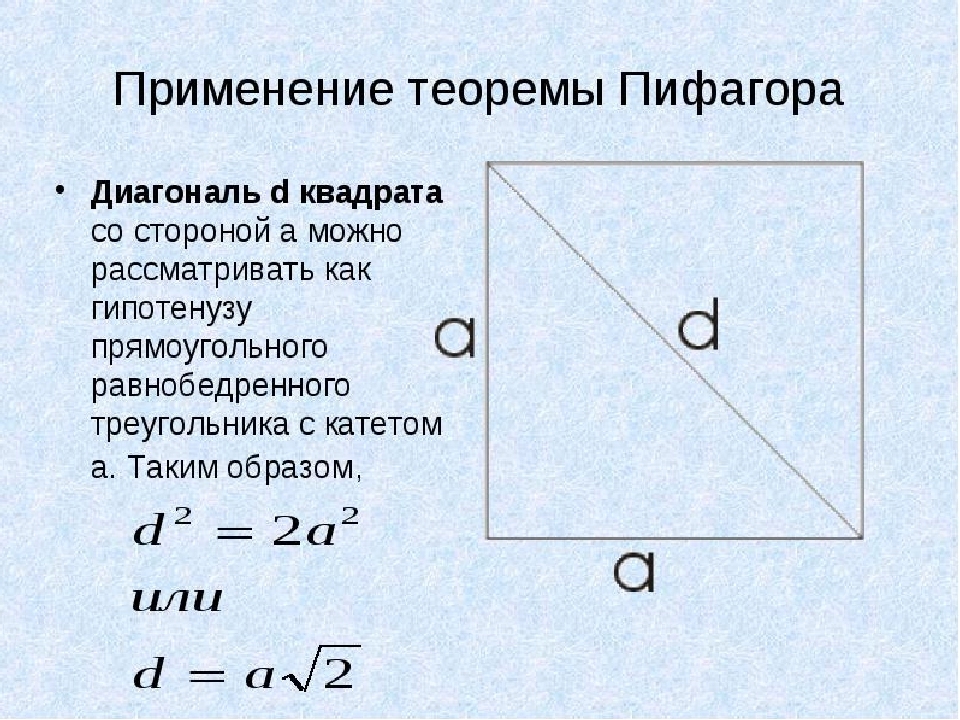
V tomto príklade použijeme vetu Pythagoras. Na štvorci sú všetky strany rovnaké a diagonálne d. Zvážime hypotenus obdĺžnikového trojuholníka Isosceles s nohou a. Teraz nájdeme štvorcový diagonálny, ak je jeho oblasť známa:

Aby sme maľovali celú pythagorovskú vetu, rozhodneme sa o druhej možnosti: d \u003d aising, kde A je strana štvorca.
Takže vieme napríklad, že oblasť štvorca sa rovná 64. Takže jedna strana a \u003d √64 \u003d 8.
Ukázalo sa D \u003d 8√2. Koreň 2 neukazuje celé číslo, takže v odpovedi môžete napísať týmto spôsobom: d \u003d 8√2. Ak však chcete vypočítať hodnotu, použite kalkulačku: √2 \u003d 1,41421356237 a vynásobte 8, ukázalo sa, že 11, 3137084.

Dôležité: V matematike zvyčajne nie sú v reakcii nezostali žiadne čísla s veľkým počtom čísel. Je potrebné zaokrúhliť alebo odísť s koreňom. Odpoveď na diagonál je preto, ak je oblasť 64 nasledovne: d \u003d 8√2.

Ako nájsť štvorcovú plochu cez uhlopriečku?

Vzorec na nájdenie štvorcovej oblasti cez diagonál je jednoduchý:

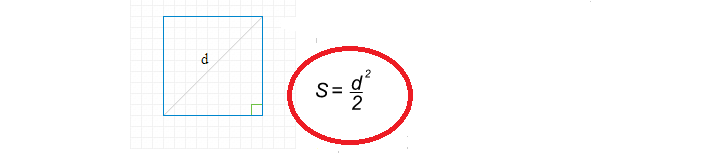
Teraz napíšeme riešenie, aby sme našli štvorcovú oblasť cez diagonál:

Diagonálna d \u003d 8.
8 na štvorec je 64.
64 Rozdeľte 2 rovnaké 32.
Štvorcová plocha je 32.

Rady: Táto úloha má ďalšie riešenie prostredníctvom vety Pythagoras, ale je zložitejšia. Preto použite riešenie, ktoré sme skúmali.

Ako nájsť štvorcovú plochu, poznáte jeho obvod?

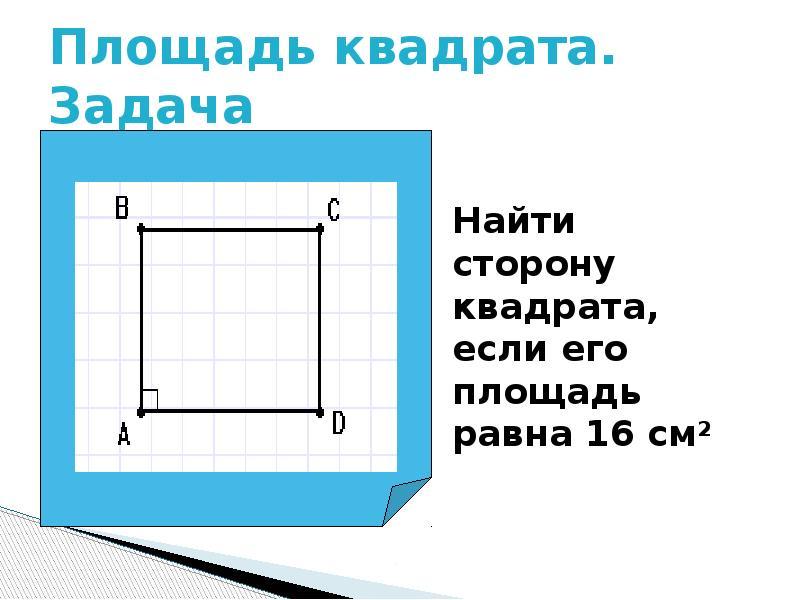
Obvod štvorcového štvorca P. - Toto je súčet všetkých strán. Ak chcete nájsť svoju oblasť, poznať jeho obvod, musíte najskôr vypočítať stranu štvorcového štvorca. Riešenie:

Predpokladajme, že obvod je 24. Rozdeľte 24 na 4 strany, ukáže sa 6 - toto je jedna strana.
Teraz používame vzorec na nájdenie oblasti, pretože vieme, čo sa strana štvorcového štvorca rovná: S \u003d a na štvorci, s \u003d 6 v štvorcových \u003d 36.
Odpoveď: 36

Ako vidíte, poznáte obvod štvorca, jednoducho nájdite jeho oblasť.

Ako nájsť oblasť štvorca vpísaného v kruhu s daným polomerom?

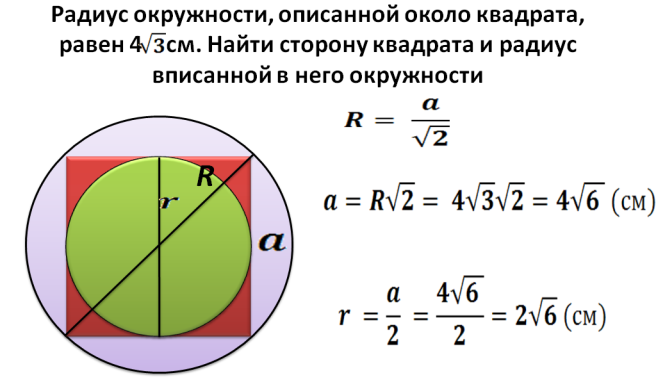
Polomer R - Toto je polovica diagonálu štvorca vpísaného v kruhu. Teraz nájdeme uhlopriečku podľa vzorca: d \u003d 2*r. Ďalej nájdeme štvorec štvorca vpísaného v kruhu s daným polomerom:

Diagonál je 2 násobený polomerom. Napríklad polomer je 5, potom je diagonál rovnaký 2*5=10.
Bolo opísané vyššie, ako nájsť štvorec štvorca, ak je známa diagonál: S \u003d diagonálna v štvorcovej štvorci rozdelenej na 2. S \u003d 10*10 a rozdeľte sa 2 \u003d 50.
Odpoveď - 50.

Táto úloha je trochu komplikovanejšia, ale tiež ľahko vyriešená, ak poznáte všetky vzorce.

Ako nájsť oblasť štvorca opísaného v blízkosti kruhu s daným polomerom?

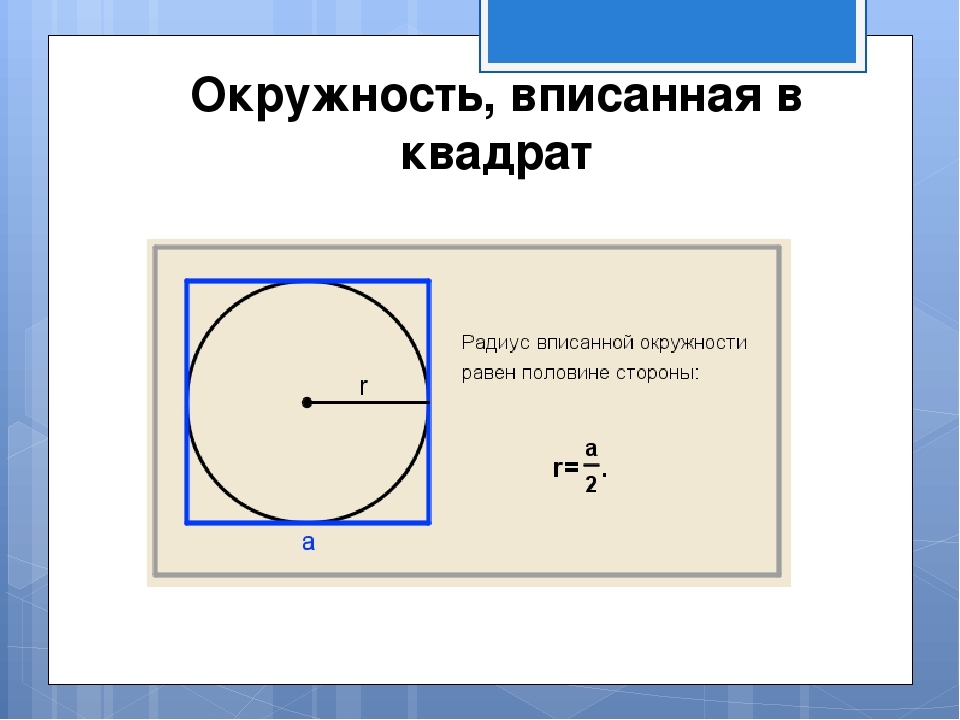
Obrázok ukazuje, že polomer vpísaného kruhu sa rovná polovici strany. Strana je umiestnená podľa spätného vzorca, ktorý je znázornený na obrázku: a \u003d 2*r. Potom zistíme oblasť štvorca opísanú v blízkosti kruhu s daným polomerom podľa vzorca S \u003d a na štvorec. Riešenie:

Predpokladajme, že polomer je 7. Strana štvorca A je 2*7 \u003d 14.
S \u003d 14 na námestí \u003d 196.

Ak pochopíte podstatu riešenia takýchto problémov, môžete ich rýchlo a jednoducho vyriešiť. Pozrime sa na niekoľko ďalších príkladov.

Príklady riešenia problémov na tému „Square Square“

Na opravu materiálu pokrytého a zapamätania si všetky vzorce je potrebné vyriešiť niekoľko príkladov problémov na tému „štvorcová oblasť“. Začneme jednoduchou úlohou a presunieme sa na riešenie zložitejšie: