Hogyan lehet kiszámítani a rombusz területét?

Ebben a cikkben megtanulja, hogyan lehet a rombusz területét különféle módszerekkel megtalálni. Ezeknek a képleteknek köszönhetően a geometriai problémákkal könnyen megoldható, mivel itt a cikk leírja, hogyan lehet kiszámítani a rombusz területét, tudva a feliratozott kör nagyobb és alsó, oldalának és átmérőjének átlós méretét A rombuszban.

Különböző képletekkel megtudhatja a rombusz területét. Elegendő megismerni ennek az ábranak és más figurák tulajdonságainak tulajdonságait, mivel a rombusz háromszögekre osztható, egyenértékű párhuzamosapóval, stb. Az alábbiakban látni fogja az ilyen képleteket. Azt is tudnia kell, hogy a rombusz és a paralelogram hogyan különbözik. A matematikai meghatározás szerint. A rombusz egy ilyen párhuzamos ábra, egyenlő oldalakkal, de a négyzettől eltérően - a rombusznak nincs egyenes szöge. De a Rhombus alján lévő két szög összege 180 fok lesz. Mindez a tudás hasznos lesz a rombusz területének kiszámításához, majd részletesebben.

Hogyan lehet kiszámítani a rombusz területét - az ábra tulajdonságait

Mielőtt kiszámítaná a rombusz területét, jobb, ha megismerkedne ezen ábra tulajdonságaival. Valójában, e jellemzők ismereteinek köszönhetően könnyebb bizonyítani egy adott képlet valószínűségét. Korábban már megemlítették, mi a Rhombus. Ez egy olyan ábra, amelynek minden oldala megegyezik az ellentétes éles és hülye sarkokkal, de nem egyenes.

A rombusz a következő tulajdonságokkal rendelkezik:

• minden oldal megegyezik egymással
• az egymással szemben fekvő sarkok szintén egyenlőek
• ennek az ábrának az átlós részei fellebbezőek, a kereszteződés pontján egyenlő szegmensekre oszlanak
• az átlók is keresztezik a rombusz közepén és derékszögben
• a figurák ellentétes oldalai nem tudnak keresztezni, még akkor sem, ha meghosszabbítják a sugarakat, párhuzamosak, mint egy párhuzamos ábra.

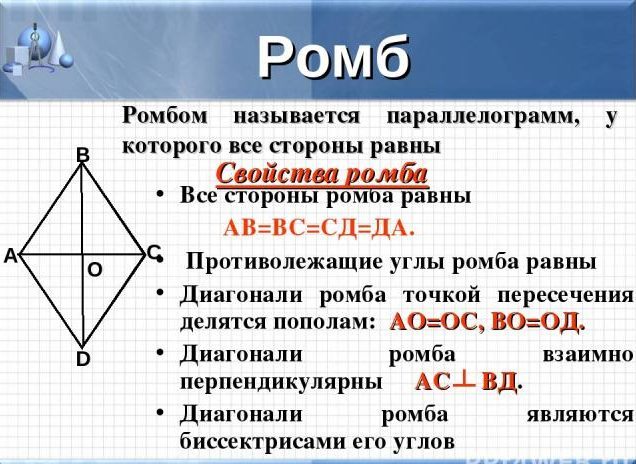
FONTOS: Felhívjuk figyelmét, hogy a rombusz négy téglalap alakú háromszögre osztható, amelyek a területen vagy két egyenlő oldalú azonos háromszöggel egyenlőek lesznek, lásd a fenti képet.

Hogyan lehet kiszámítani a rombusz területét?

Tehát, derítsük ki, hogyan kiszámítják a Rhombus területét. Használjuk ki a téglalap területének képletét, ahol:

• S \u003d a • bahol A, B a téglalap oldala.

Úgy, hogy egyértelmű, hogyan lehet eltávolítani a rombusz területének képletét ebből a képletből, lásd magyarázat:

1. Rajzoljon egy rombuszt, tegyen magasságot a BH rombusz alapjához.
2. A D ponttól a hirdetési vonalig húzzon egy CH1 magasságot is.
3. Kiderül, hogy az ABH háromszög és a CH1D háromszög egyenlő egymással, két közös oldalon, olc a fedélben.
4. Tehát AH \u003d DH1. A kapott négyzet területe megegyezik a rombusz területével
5. Tehát BH • HH1 - Ez a rombusz területe, más szóval, a BH Rombus munkája az AD oldalán, és a rombusz területe lesz, mivel a HH1 \u003d BC, és BH a magasság.

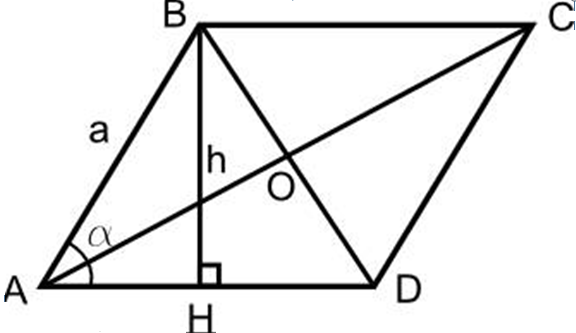
Ebből a bizonyítékból következik, hogy:

• S rombus \u003d a • h és négyzet alakú egységekben mérve.

Hogyan lehet megtalálni a rombusz területét, ismerve a geometriai alak sarkát és oldalát?

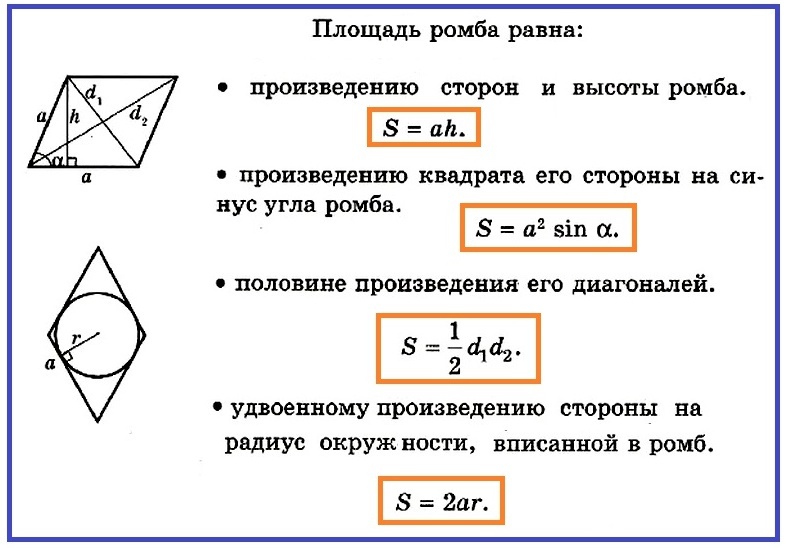
Most már tudjuk, hogy néz ki a Rhombus terület képlete, megtalálhatunk egy Rhomba területet ugyanazon a képleten, tudva, hogy a rombusz oldala megegyezik a rombusz oldalával, például éles, mint az alapon, mint Az alábbi fotó.

• S \u003d a • h

De a mi esetünkben a rombusz magasságában ismeretlenek vagyunk, meg kell találni. Ehhez meg kell fontolnia egy téglalap alakú háromszöget, amely kiderült, amikor a magasságot a rombusz alapjába vonják.

Ebben a háromszögben ismert hypotenuse és ilva. A teljes ábra területének kiszámításához magasságot kell találnia. A h \u003d a • sin. Tehát S egy egyenlő oldalú párhuzamos ábra (rombusz) területe:

• S \u003d a • a • sin ők ax \u003d a² • sinown.

Hogyan lehet kiszámítani a rombusz területét, tudva annak átlóját?

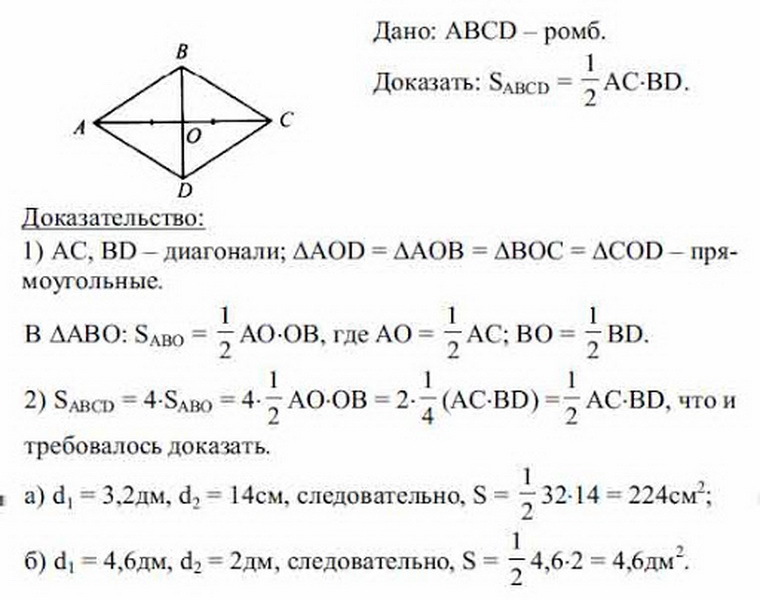
A rombusz területének képletének megismeréséhez, ha csak (a, b) átlóval ismertek, a következő példát kell figyelembe venni. A BCDA -t kapják - Rombus és tudja, mi az átlók egyenlőek. Most meg kell találni egy egyenlő oldalú párhuzamos oldalt az átlók szempontjából.

Korábban a rombusz tulajdonságait már figyelembe vették. A rombusz átlóságai egyenlőek, a kereszteződés pontján egyenlő szegmensekre osztódnak. Ebből ebből következik, hogy az összes háromszög, amelyet az ábrán feliratoznak, mindkét átlós kereszteződés eredményeként, szintén megegyezik egymással, és téglalap alakúak (három oldalról). A rombusz területének megtalálásához elegendő egy háromszög területének megtalálása és a 4 -es adatok szorzásához.

Összesen kiderül, hogy:

• S rombus \u003d 4 (1/2 ao • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Total Square S ROMM \u003d munka A • B (átlók) osztva kettővel: S \u003d 1/2 A • B

Hogyan lehet kiszámítani a rombusz területét, ismerve annak oldalát és a benne feliratozott kör sugarat?

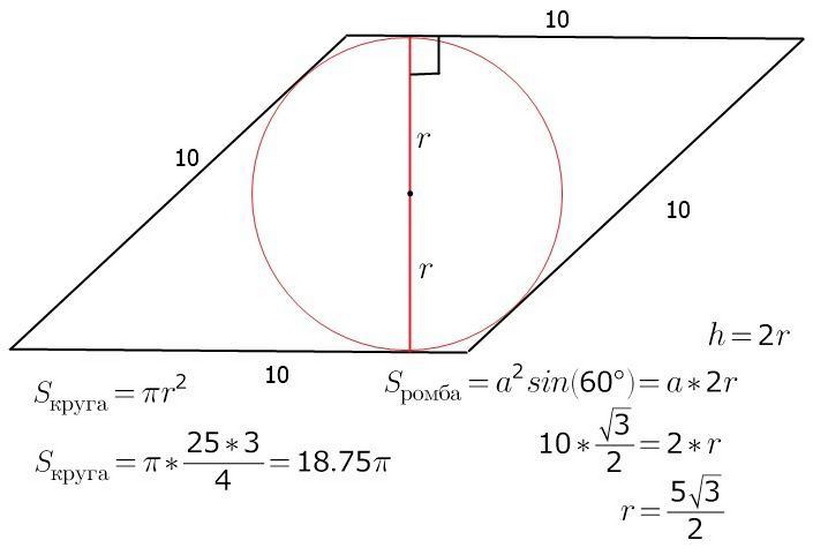
A rombusz területét kiszámíthatjuk az r - sureus és a - az ábra oldalának hosszával. Már ismert, hogy S - az ábra területe megegyezik a B munkával - a H -magasság oldalán. A kör közepén keresztül az A, B kereszteződési központ is a rombusz átlós. Végezze el a magasságot és ugyanakkor a rombusz átmérőjét. A kép azt mutatja, hogy az ábra magassága a kör két sugara. Most könnyű megtalálni maga a rombusz területét:

• S \u003d a • h \u003d a • 2r

Az alábbiakban lásd a témában szereplő feladat példáját.

Még mindig lássa az ilyen cikkeket erről a témáról itt:

1. A téglalap területe, hogyan lehet megtalálni?
2. Hogyan lehet megtalálni egy kör területét?
3. Négyzet alakú terület - képletek.

Videó: Példa a rombusz területének kiszámítására