Hogyan lehet megtalálni egy négyzet alakú területet, ha a kerület ismert, átlós? Hogyan lehet megtalálni a körbe beillesztett négyzet négyzetét, és a kerület közelében leírhatjuk: képlet, a problémák megoldásának példái. Hogyan lehet megtalálni a négyzet oldalát és átlókat, ha a területe ismert?

Olvassa el a cikket, hogy megtudja, hogyan lehet a négyzet alakú területet különböző módon megtalálni.

A négyzet egyenlő oldalú téglalap. Ennek a megfelelő és lapos négyszögnek minden oldalán, sarkában és átlókban egyenlősége van. Annak a ténynek köszönhetően, hogy van ilyen egyenlőség, a terület és más jellemzők kiszámításának képlete kissé módosul, mint a többi matematikai adatok. De ez nem teszi túl bonyolult feladatokat. Elemezzük a cikk összes képletét és megoldását.

Hogyan lehet megtalálni a tér oldalát, tudva annak területét?

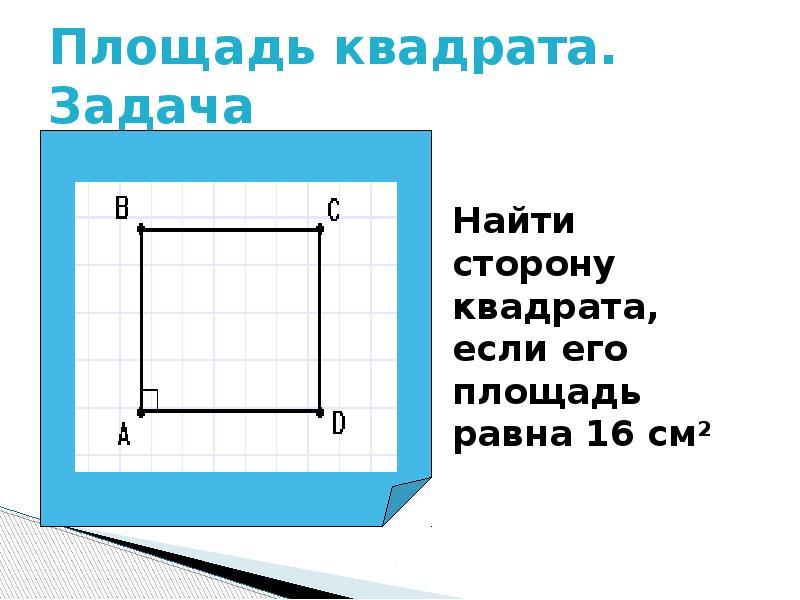
Négyzet S. A közvetlen és a négyzet négyzeteket a képlettel számolják: A Szorozva b.- Mivel azonban a térnek a felek teljes egyenlősége van, a területe egyenlő lesz: S \u003d (a) a második fokozatban.  Hogyan lehet megtudni a tér oldalának méretét, tudva annak területét?

• Ha a négyzet négyzet területe ismert, akkor az oldalt úgy találjuk meg, hogy kiszámítjuk a területet a négyzetgyök alatt.
• Például a négyzet területe 49, akkor mi az oldal?
• 49 \u003d (a) a második fokozatban- Megoldás: a \u003d 49 \u003d 7 gyökere. Válasz: 7.

Ha meg kell találnia a négyzet négyzet oldalát, amelynek területe túl hosszú, akkor használja a számológépet. Először tárcsázza a terület számát, majd nyomja meg a gyökérjelet a számológép billentyűzetén. A kapott szám lesz a válasz.

Hogyan lehet megtalálni egy négyzet alakú átlót, ha a területe ismert?

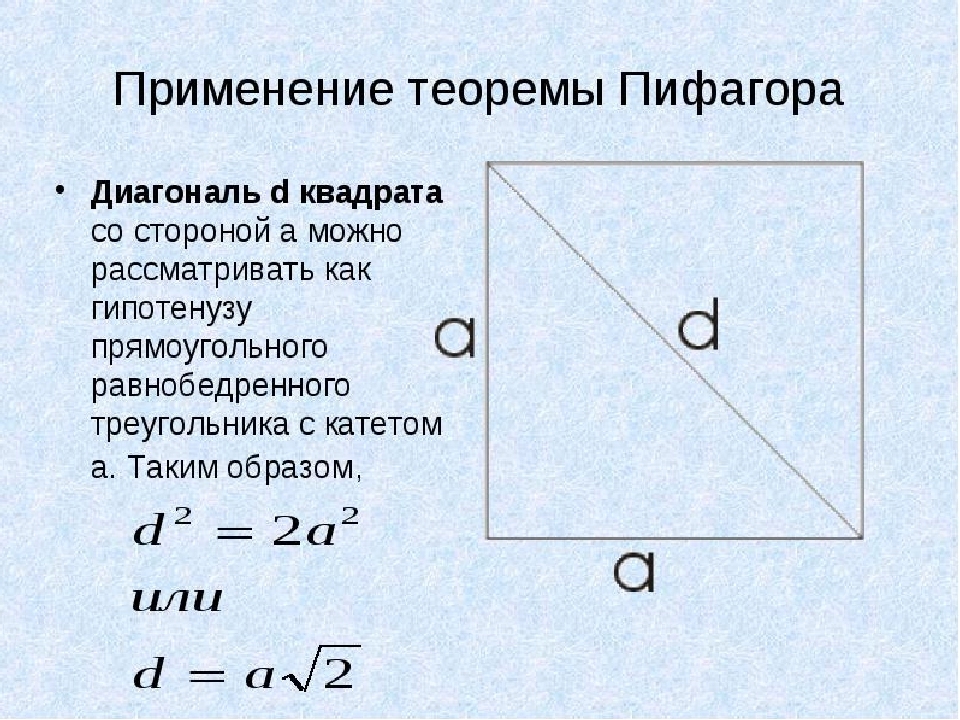
Ebben a példában a Pythagoras tételt fogjuk használni. Egy négyzetben minden oldal egyenlő, és az átlós d. A lábú téglalap alakú egyenlő háromszög hipotenuszának tekintjük a- Most egy négyzet alakú átlót találunk, ha a területe ismert:

• Annak érdekében, hogy ne festsük a teljes Pythagorean -tételt, a második lehetőségről döntünk: d \u003d aisis, ahol A a négyzet oldala.
• Tehát ismerjük például a tér területét, ez egyenlő 64 -nek. Tehát az egyik oldal a \u003d √64 \u003d 8.
• Kiderül D \u003d 8√2- A 2 gyökere nem adja ki az egész számot, tehát a válaszban így írhat: d \u003d 8√2- De ha kiszámítani szeretné az értéket, akkor használja a számológépet: √2 \u003d 1,41421356237, és szaporítsuk meg 8 -mal, kiderül, hogy 11, 3137084.

Fontos: Általában a matematikában nem maradnak nagy számú számmal rendelkező szám. A gyökérrel kell kerekíteni vagy elhagyni. Ezért az átlós válasz az, ha a terület 64 a következőképpen: d \u003d 8√2.

Hogyan lehet megtalálni egy négyzet alakú területet egy átlón keresztül?

A négyzet területének átlós területének megtalálásának képlete egyszerű:

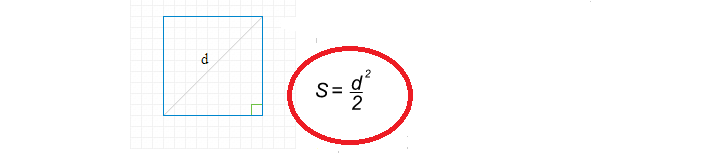
Most írjunk egy megoldást, hogy megtalálják a négyzet alakú területet az átlósokon keresztül:

• Átlós D \u003d 8.
• 8 A négyzetben 64.
• 64 Ossza meg 2 egyenlő 32 -et.
• A négyzet alakú terület 32.

Tanács: Ennek a feladatnak egy másik megoldása van a Pythagoras -tételen keresztül, de összetettebb. Ezért használja a megvizsgált megoldást.

Hogyan lehet megtalálni egy négyzet alakú területet, tudva annak kerületét?

A négyzet alakú kerülete P. - Ez az összes fél összege. Ahhoz, hogy megtalálja a területét, tudva annak kerületét, először ki kell számolni a négyzet négyzet oldalát. Megoldás:

• Tegyük fel, hogy a kerület 24. Ossza meg a 24 -et 4 oldalra, kiderül 6 - ez az egyik oldal.
• Most a képletet használjuk a terület megtalálásához, tudva, hogy a négyzet négyzet oldala egyenlő: S \u003d a négyzetben, s \u003d 6 négyzetben \u003d 36.
• Válasz: 36

Mint láthatja, a tér kerületének ismerete, csak keresse meg annak területét.

Hogyan lehet megtalálni egy adott sugarú körbe beillesztett négyzet területét?

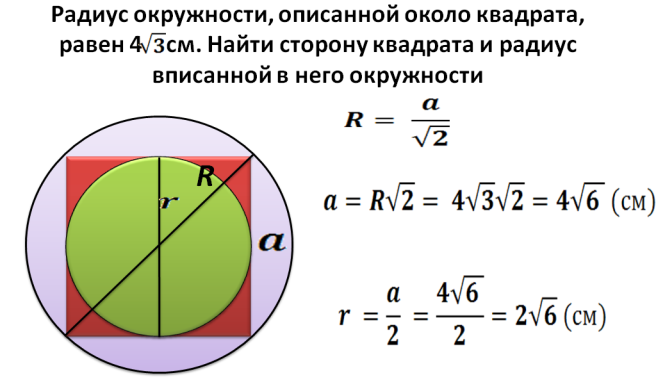
Sugár R -tól - Ez egy körbe felírt négyzet átlósának fele. Most megtalálhatunk egy átlót a képlet szerint: d \u003d 2*r- Ezután megtaláljuk a négyzet négyzetét, amely egy adott sugarú körbe van beírva:

• Az átló 2 szorzódik a sugarakkal. Például a sugara 5, akkor az átlós egyenlő 2*5=10.
• A fentiekben leírták, hogyan lehet megtalálni a négyzet négyzetét, ha az átlós ismert: S \u003d átló egy négyzetben, oszlik 2 -re. S \u003d 10*10, és oszlik 2 \u003d 50 -rel.
• Válasz - 50.

Ez a feladat egy kicsit bonyolultabb, de könnyen megoldható, ha ismeri az összes képletet.

Hogyan lehet megtalálni egy adott sugarú kör közelében leírt négyzet területét?

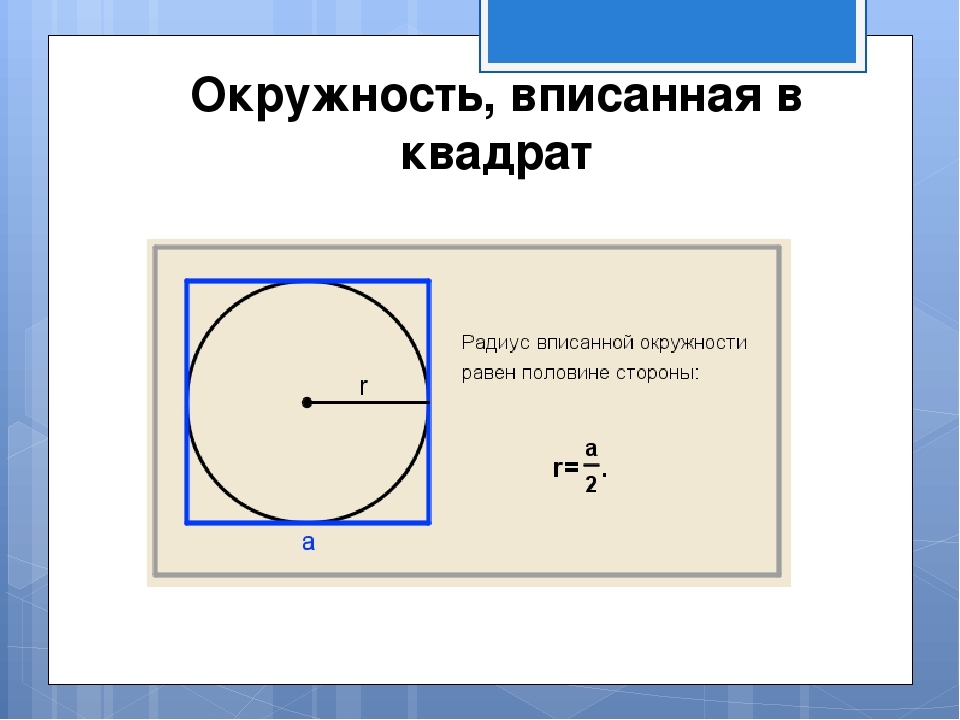
A kép azt mutatja, hogy a feliratozott kör sugara megegyezik az oldal felével. Az oldal a képen ábrázolt fordított képlet szerint található: a \u003d 2*r- Ezután megtaláljuk a kör közelében leírt négyzet területét, amely egy adott sugarral rendelkezik a képlet szerint S \u003d és egy négyzetben- Megoldás:

• Tegyük fel, hogy a sugár 7. Az A négyzet oldala 2*7 \u003d 14.
• S \u003d 14 négyzetben \u003d 196.

Ha megérti az ilyen problémák megoldásának lényegét, akkor gyorsan és egyszerűen megoldhatja azokat. Nézzünk meg néhány további példát.

Példák a "Square Square" témájának problémáinak megoldására

A fedett anyag rögzítéséhez és az összes képlet emlékezéséhez több példát kell megoldani a „négyzet alakú terület” témájának problémáira. Egy egyszerű feladattal kezdjük, és a bonyolultabb megoldáshoz lépünk:

Most már tudja, hogyan kell használni a négyzet négyzetének képletét, ami azt jelenti, hogy bármilyen feladatot elvégezhet. Siker a jövőbeli képzésben!

Videó: A négyzetterület kiszámítása