Jak vypočítat oblast kosočtverce?

V tomto článku se naučíte, jak najít kosočtvercovou oblast s různými metodami. Díky těmto vzorcám bude snadno vyřešeno problémy s geometrií, protože zde článek popisuje, jak vypočítat oblast kosočtverce, protože vědí velikost diagonálu větších a menších, úhlů a průměru Napsaný kruh v kosočtcombusu.

Oblast kosočtverce najdete různými vzorci. Stačí znát vlastnosti tohoto obrázku a vlastností jiných čísel, protože kosočtverce lze rozdělit na trojúhelníky, lze jej přirovnat k rovnoběžnosti atd. Níže uvidíte takové vzorce. Musíte také vědět, jak se liší kosočtvercový a paraleglogram. Podle matematické definice. Kosočtverce je postavou takového rovnoběžníku se stejnými stranami, ale na rozdíl od čtverce - kosočtverce nemá rovné úhly. Součet dvou úhlů na základně kosočtverce však bude 180 stupňů. Všechny tyto znalosti se hodí pro výpočet oblasti kosočtverce, poté podrobněji.

Jak vypočítat oblast kosočtverce - vlastnosti obrázku

Před výpočtem oblasti kosočtverce je lepší seznámit se s vlastnostmi tohoto obrázku. Ve skutečnosti, díky znalosti těchto charakteristik, bude snazší prokázat pravděpodobnost konkrétního vzorce. Dříve to již bylo zmíněno, co je kosočtverce. Jedná se o postavu s rovnou všech stranách rovných opačným ostrým a hloupým rohům, ale ne rovným.

Kosočtverce má následující vlastnosti:

• všechny strany se navzájem rovnají
• rohy ležící proti sobě jsou také stejné
• diagonály tohoto obrázku jsou bisektory, v průsečíku jsou rozděleny do stejných segmentů
• diagonály se také protínají ve středu kosočtverce a v pravém úhlu
• opačné strany obrázků se nemohou protínat, i když rozšiřujete paprsky, jsou paralelní, jako rovnoběžník.

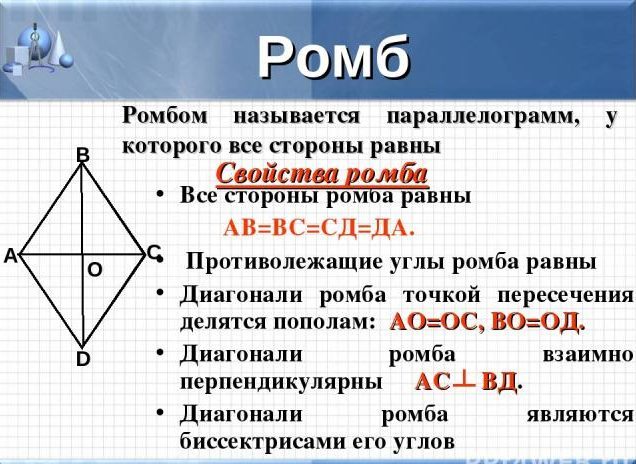
DŮLEŽITÉ: Vezměte prosím na vědomí, že kosočtverce lze rozdělit do čtyř obdélníkových trojúhelníků, které budou stejné v oblasti nebo dvěma rovnostranný identický trojúhelníky, viz výše uvedený obrázek.

Jak vypočítat oblast kosočtverce?

Pojďme tedy zjistit, jak se vypočítá oblast kosočtverce. Využijte vzorec pro oblast obdélníku, kde:

• S \u003d a • bkde a, b jsou strany obdélníku.

Aby bylo najevo, jak získat vzorec kosočtverce z tohoto vzorce, vzorec oblasti, viz vysvětlení:

1. Nakreslete kosočtverce, udělejte výšku na základnu kosočtverce BH.
2. Z bodu D k ad linii také nakreslete výšku CH1.
3. Ukazuje se, že trojúhelník ABH a trojúhelník CH1D se navzájem rovná na dvou společných stranách, ∠ mezi nimi.
4. Takže ah \u003d dh1. Oblast výsledných čtverců se bude rovnat oblasti kosočtverce
5. Takže BH • HH1 je oblast kosočtverce, jinými slovy, díla nadmořské výšky BH na stranu reklamy a bude oblastí kosočtverce, protože Hh1 \u003d BC a BH je výška .

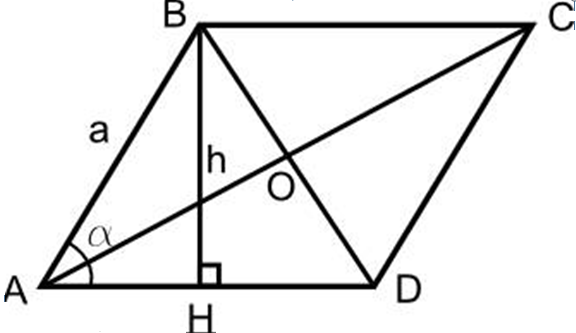
Vyplývá z důkazu, že:

• S Rhombus \u003d A • H a měřeno v čtvercových jednotkách.

Jak najít oblast Romb, znát roh a stranu geometrické postavy?

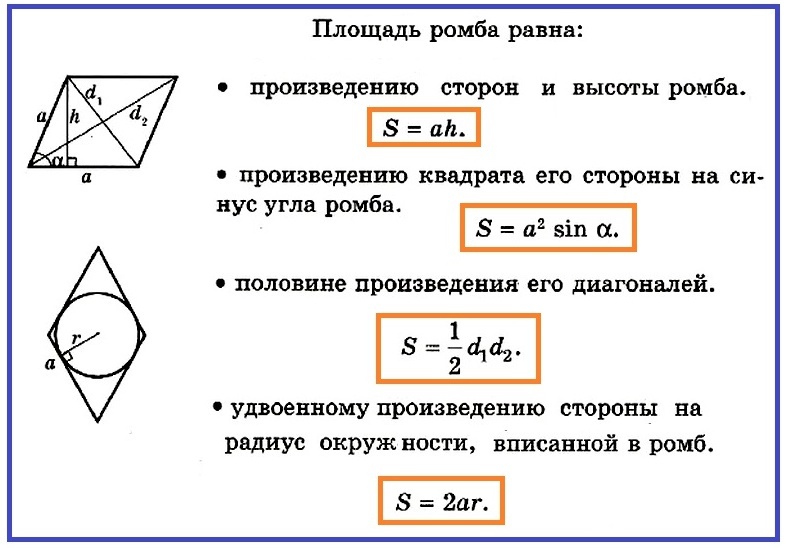
Nyní víme, jak vypadá vzorec oblasti kosočtverce, můžeme najít oblast Rhomba na stejném vzorci, protože víme, co je strana kosočtverce stejná jako strana kosočtverce, například ostrý, jako v základně Fotografie níže.

• S \u003d a • h

V našem případě však nejsme známí výškou kosočtverce, mělo by to být nalezeno. Chcete -li to provést, budete muset zvážit obdélníkový trojúhelník, který se ukázal, když byla výška přitahována na základnu kosočtverce.

V tomto trojúhelníku je známo hypotenus a ∠α. Chcete -li vypočítat oblast celé postavy, budete muset najít výšku. A h \u003d A • Sin. Takže je oblast rovnostranného rovnoběžníku (kosočtverce):

• S \u003d a • a • hřích ax \u003d a² • hřích.

Jak vypočítat oblast kosočtverce a znát její diagonály?

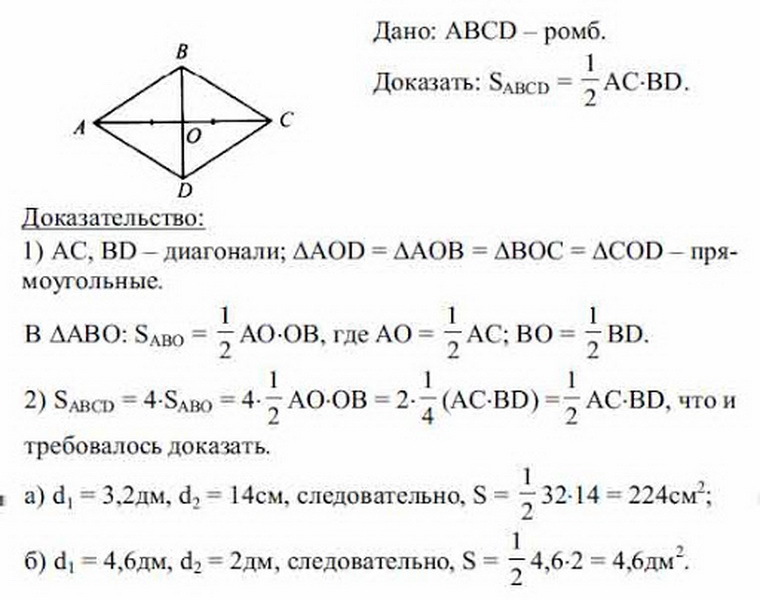
Chcete -li zjistit vzorec oblasti kosočtverce, pokud jsou známy pouze diagonály (a, b), je třeba zvážit následující příklad. BCDA je dána - kosočtverce a ví, co jsou diagonály stejné. Nyní je nutné najít oblast S rovnostranného rovnoběžníku z hlediska diagonálů.

Dříve byly vlastnosti kosočtverce již zváženy. Diagonály kosočtverce jsou stejné, v průsečíku jsou rozděleny do stejných segmentů. Z toho vyplývá, že všechny trojúhelníky, které jsou napsány na obrázku v důsledku průniku obou úhlopříčků, jsou také navzájem rovny a jsou obdélníkové (na třech stranách). Pro nalezení oblasti kosočtverce stačí najít oblast jednoho trojúhelníku a vynásobit data získaná 4.

Celkem se ukáže, že:

• S Rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Celkový čtvercový s Romm bude \u003d práce a • b (diagonály) děleno dvěma: S \u003d 1/2 a • b

Jak vypočítat oblast kosočtverce, znát její stranu a poloměr kruhu v ní?

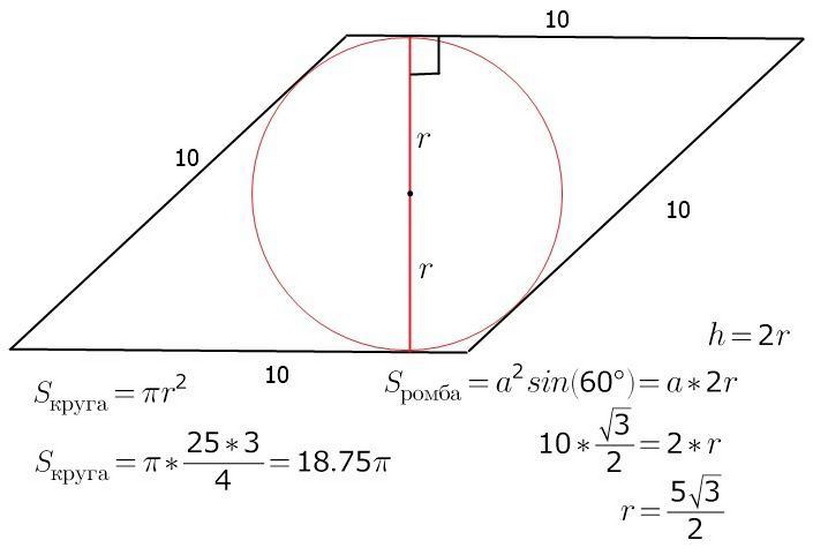
Oblast Rhomby lze vypočítat známým R - poloměrem a A - délkou strany obrázku. Již je známo, že S - oblast postavy bude rovná dílo B - strana na výšce H -. Přes střed kruhu to bude také průsečík A, B je diagonály kosočtverce. Proveďte výšku a současně průměr kosočtverce. Obrázek ukazuje, že výška obrázku je dva poloměry kruhu. Nyní bude snadné najít oblast samotného kosočtverce:

• S \u003d a • h \u003d a • 2r

Níže viz příklad úkolu na toto téma.

Stále viz takové články na toto téma zde:

1. Oblast obdélníku, jak najít?
2. Jak najít oblast kruhu?
3. Čtvercová oblast - vzorce.

Video: Příklad toho, jak vypočítat oblast kosočtverce