Jak najít čtvercovou oblast, pokud je obvod znám, diagonální? Jak najít čtverec čtverce napsaný v kruhu a popsaný v blízkosti obvodu: vzorec, příklady řešení problémů. Jak najít stranu a úhlopříčku náměstí, pokud je její oblast známa?

Přečtěte si článek, abyste věděli, jak najít čtvercovou oblast různými způsoby.

Obsah

Čtverec je rovnostranný obdélník. Tento řádný a plochý čtyřúhelník má rovnost ve všech stranách, rozích a úhlopříčkách. Vzhledem k tomu, že existuje taková rovnost, je vzorec pro výpočet oblasti a další charakteristiky ve srovnání s jinými matematickými čísly mírně modifikován. To však neznamená příliš komplikované úkoly. Pojďme analyzovat všechny vzorce a řešení tohoto článku.

Jak najít stranu čtverce a znát její oblast?

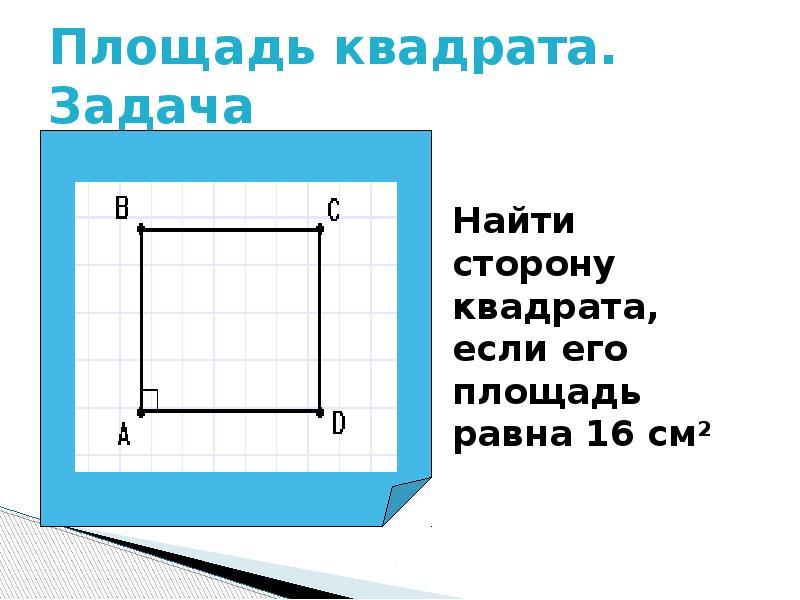
Náměstí S. Přímé a čtvercové čtverce se počítají podle vzorce: A Vynásobte b.. Ale protože náměstí má úplnou rovnost stran, jeho oblast bude stejná: S \u003d (a) ve druhém stupni.Jak zjistit velikost strany čtverce a znát jeho oblast?

Pokud je známa plocha čtvercového čtvercového čtverce, najdeme stranu výpočtem oblasti zpod druhá odmocnina.
Například plocha čtverce je 49, k čemu je strana stejná?
49 \u003d (a) ve druhém stupni. Řešení: a \u003d kořen 49 \u003d 7. Odpověď: 7.

Pokud potřebujete najít stranu čtvercového čtverce, její oblast je příliš dlouhá, použijte kalkulačku. Nejprve vytočte číslo oblasti a poté stiskněte kořenovou značku na klávesnici kalkulačky. Výsledné číslo bude odpověď.

Jak najít čtvercovou úhlopříčku, pokud je její oblast známa?

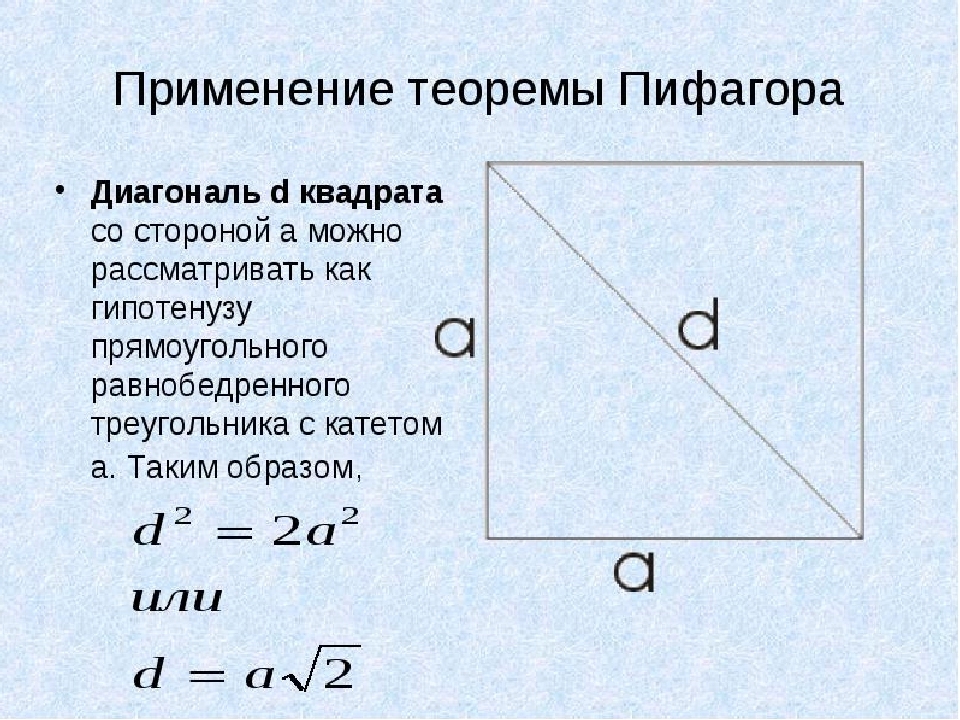
V tomto příkladu použijeme větu Pythagoras. Na čtverci jsou všechny strany stejné a diagonálně d. Budeme uvažovat o hypotenu obdélníkového trojúhelníku isosceles s nohou a. Nyní najdeme čtvercovou úhlopříčku, pokud je její oblast známa:

Abychom nemohli malovat celou Pythagorovu větu, rozhodneme se pro druhou možnost: d \u003d aising, kde A je stranou čtverce.
Známe tedy například oblast náměstí, rovná se 64. Takže jedna strana a \u003d √64 \u003d 8.
Ukázalo se to D \u003d 8√2. Kořen 2 nevykazuje celé číslo, takže v odpovědi můžete napsat tímto způsobem: d \u003d 8√2. Pokud však chcete vypočítat hodnotu, použijte kalkulačku: √2 \u003d 1,41421356237 a vynásobte 8, ukáže se 11, 3137084.

Důležité: Obvykle, v matematice, nejsou v reakci ponechána žádná čísla s velkým počtem čísel. Je nutné zaokrouhlit nebo odejít s kořenem. Odpověď na diagonálu je proto, zda je oblast 64 následujícím způsobem: d \u003d 8√2.

Jak najít čtvercovou oblast prostřednictvím diagonálu?

Vzorec pro nalezení čtvercové oblasti přes úhlopříčku je jednoduchý:

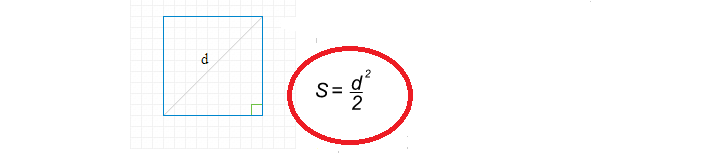
Nyní napíšeme řešení, jak najít čtvercovou oblast prostřednictvím úhlopříčky:

Diagonální D \u003d 8.
8 Na náměstí je 64.
64 Rozdělte 2 rovnými 32.
Čtvercová plocha je 32.

Rada: Tento úkol má další řešení prostřednictvím věty Pythagoras, ale je složitější. Proto použijte řešení, které jsme zkoumali.

Jak najít čtvercovou oblast a znát její obvod?

Obvod čtvercového čtverce P. - Toto je součet všech stran. Chcete -li najít její oblast, znát její obvod, musíte nejprve vypočítat stranu čtvercového čtverce. Řešení:

Předpokládejme, že obvod je 24. Rozdělte 24 na 4 strany, ukáže se 6 - to je jedna strana.
Nyní používáme vzorec pro nalezení oblasti a víme, co se na straně čtvercového čtverce rovná: S \u003d a na čtverci, s \u003d 6 na čtverci \u003d 36.
Odpovědět: 36

Jak vidíte, znát obvod čtverce, najděte jeho oblast.

Jak najít oblast čtverce napsané v kruhu s daným poloměrem?

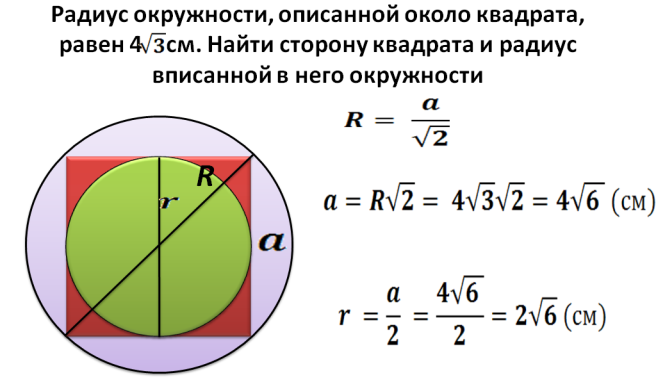
Poloměr R - Toto je polovina úhlopříčky čtverce napsaného v kruhu. Nyní najdeme diagonálu podle vzorce: d \u003d 2*r. Dále najdeme čtverec čtverce napsaný v kruhu s daným poloměrem:

Úhlopříčka je 2 násobení poloměrem. Například poloměr je 5, pak je diagonála stejná 2*5=10.
Bylo popsáno výše, jak najít čtverec čtverce, pokud je známa úhlopříčka: S \u003d diagonálně na čtverci rozděleném na 2. s \u003d 10*10 a vydělte 2 \u003d 50.
Odpovědět - 50.

Tento úkol je trochu komplikovanější, ale také snadno vyřešen, pokud znáte všechny vzorce.

Jak najít oblast čtverce popsané poblíž kruhu s daným poloměrem?

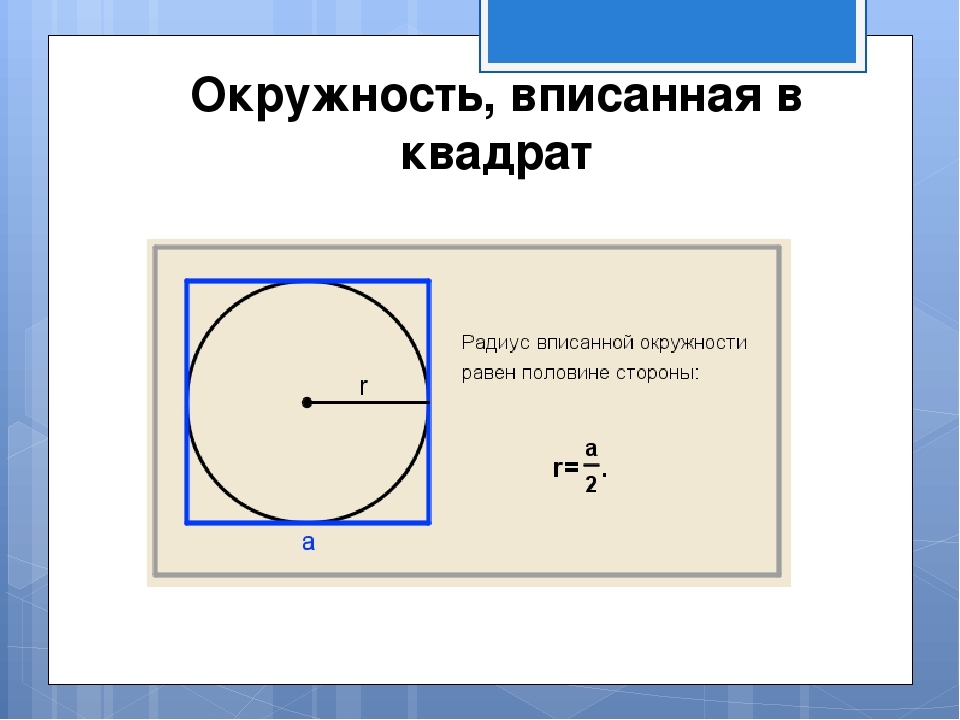
Obrázek ukazuje, že poloměr napsaného kruhu se rovná polovině strany. Strana je umístěna podle reverzního vzorce, který je znázorněn na obrázku: a \u003d 2*r. Pak najdeme oblast čtverce popsanou v blízkosti kruhu s daným poloměrem podle vzorce S \u003d a na čtverci. Řešení:

Předpokládejme, že poloměr je 7. Strana čtverce A je 2*7 \u003d 14.
S \u003d 14 na čtverci \u003d 196.

Pokud rozumíte podstatě řešení takových problémů, můžete je vyřešit rychle a jednoduše. Podívejme se na několik dalších příkladů.

Příklady řešení problémů na téma „Square Square“

Pro opravu krytého materiálu a zapamatování si všech vzorců je nutné vyřešit několik příkladů problémů na téma „čtvercové oblasti“. Začínáme jednoduchým úkolem a přecházíme k řešení složitějšího: