Hur beräknar jag området för romb?

I den här artikeln kommer du att lära dig att hitta området i romb med olika metoder. Tack vare dessa formler kommer det lätt att lösas genom geometriproblem, för här kommer artikeln att beskriva hur man beräknar rombens yta, och vet storleken på diagonalen i större och lägre, sida och diameter på den inskrivna cirkeln i romb.

Du kan ta reda på området för romb med olika formler. Det räcker med att känna till egenskaperna hos denna figur och egenskaper hos andra figurer, eftersom romb kan delas upp i trianglar, det kan likställas med ett parallellogram etc. Nedan ser du sådana formler. Du måste också veta hur romb och ett parallellogram skiljer sig åt. Enligt den matematiska definitionen. Rhombus är en figur av ett sådant parallellogram med lika sidor, men till skillnad från torget - har romben inga raka vinklar. Men summan av de två vinklarna vid basen av romb kommer att vara 180 grader. All denna kunskap kommer att vara praktiskt för att beräkna rombområdet och sedan mer detaljerat.

Hur man beräknar rombområdet - figurens egenskaper

Innan rombens område är bättre att bekanta dig med egenskaperna för denna figur. Tack vare kunskap om dessa egenskaper kommer det faktiskt att vara lättare att bevisa sannolikheten för en viss formel. Tidigare nämndes det redan vad Rhombus är. Det är en figur med lika med alla sidor som är lika med motsatta skarpa och dumma hörn, men inte raka.

Rhombus har följande egenskaper:

• alla sidor är lika med varandra
• hörnen som ligger mittemot varandra är också lika
• diagonalerna i denna figur är bisektorer, vid korsningspunkten är uppdelade i lika segment
• diagonalerna korsar också i mitten av romb och i vinklar
• de motsatta sidorna av figurerna kan inte korsa varandra, även om du utvidgar strålarna är de parallella, som ett parallellogram.

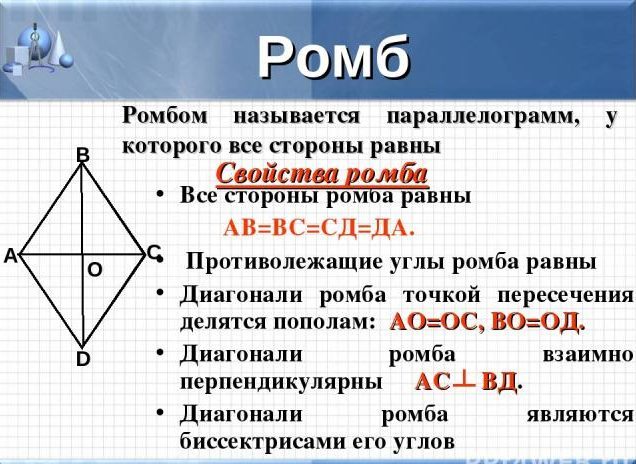
VIKTIG: Observera att romb kan delas upp i fyra rektangulära trianglar, som kommer att vara lika i området, eller med två liksidiga identiska trianglar, se bilden ovan.

Hur beräknar jag området för romb?

Så låt oss ta reda på hur rombområdet beräknas. Låt oss dra nytta av formeln för rektangelns område, där:

• S \u003d a • bdär a, b är sidorna på rektangeln.

Så att det är tydligt hur man tar bort formeln för rombområdet från denna formel, se förklaring:

1. Rita en romb, gör en höjd till basen av BH -romb.
2. Från punkt D till annonslinjen drar också en CH1 -höjd.
3. Det visar sig att triangeln ABH och triangeln CH1D är lika med varandra på två vanliga sidor, ∠ i locket mellan dem.
4. Så ah \u003d dh1. Området på det resulterande torget kommer att vara lika med rombområdet
5. Så BH • HH1 - Detta är rombens område, med andra ord, arbetet med BH -romb till sidan av AD och kommer att vara romb, eftersom HH1 \u003d BC och BH är det höjd.

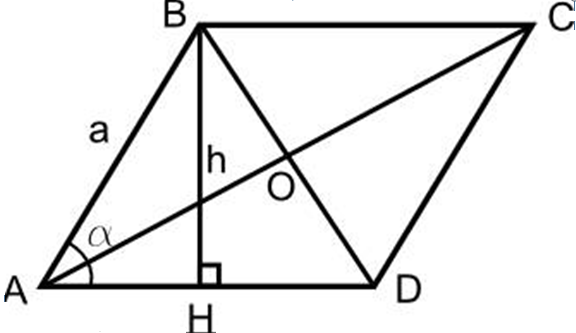
Det följer av beviset att:

• S rhombus \u003d a • h och mätt i fyrkantiga enheter.

Hur hittar man området i romb, känner till hörnet och sidan av den geometriska figuren?

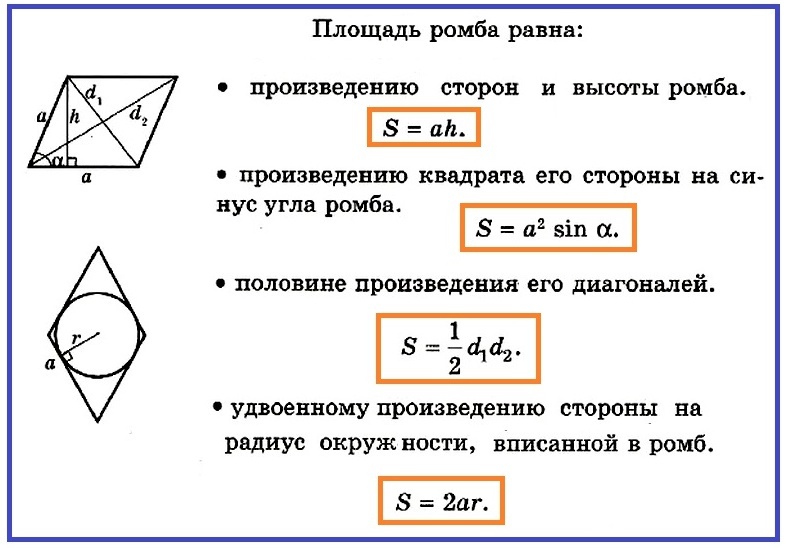
Nu vet vi hur formeln för rombområdet ser ut, vi kan hitta ett rombområde på samma formel, veta vad sidan av romben är lika med rombens sida, till exempel skarp vid basen, som i Bilden nedan.

• S \u003d a • h

Men i vårt fall är vi okända för rombens höjd, det bör hittas. För att göra detta måste du överväga en rektangulär triangel, som visade sig när höjden drogs till basen av romb.

I denna triangel är det känt hypotenus och ∠α. För att beräkna området för hela figuren måste du hitta en höjd. MEN h \u003d a • synd de. Så området för ett liksidigt parallellogram (romb) är:

• S \u003d a • a • sin de ax \u003d a² • Sinown.

Hur beräknar man området för romb, känner till dess diagonaler?

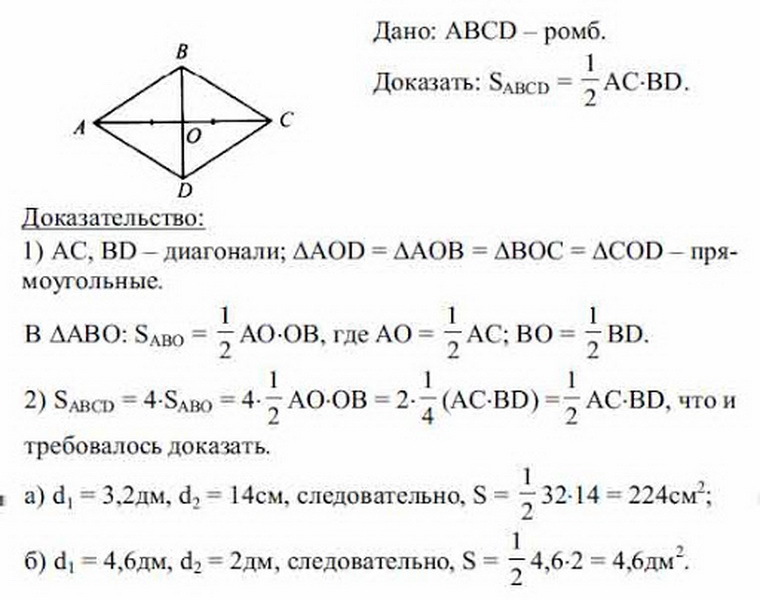
För att ta reda på formeln för rombområdet, när endast (a, b) diagonaler är kända, bör följande exempel övervägas. BCDA ges - romb och vet vad diagonalerna är lika. Nu är det nödvändigt att hitta S -område i ett liksidigt parallellogram i termer av diagonaler.

Tidigare beaktades redan egenskaperna hos romben. Rombens diagonaler är lika, vid korsningspunkten är de uppdelade i lika segment. Från detta följer att alla trianglar som är inskrivna i figuren som ett resultat av skärningspunkten mellan båda diagonalerna också är lika med varandra och de är rektangulära (på tre sidor). För att hitta rombens område räcker det att hitta området för en triangel och multiplicera de data som erhållits av 4.

Totalt visar det sig att:

• S Rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Total Square S romm kommer att vara \u003d arbeta A • B (diagonaler) dividerat med två: S \u003d 1/2 a • b

Hur beräknar man rombområdet, känner till dess sida och cirkelns radie som är inskriven i den?

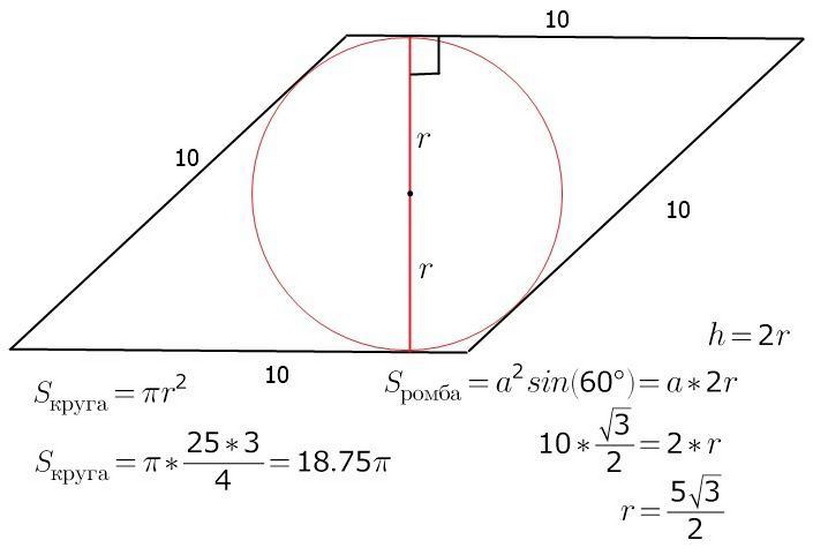
Rombområdet kan beräknas genom att känna till r - radie och a - längden på figurens sida. Det är redan känt att s - figurens område kommer att vara lika med arbetet b - sidan på h - höjd. Genom mitten av cirkeln kommer det också att vara korsningens centrum A, B är rombens diagonaler. Utför höjden och samtidigt rombens diameter. Bilden visar att figurens höjd är två radier i cirkeln. Nu kommer det att vara lätt att hitta området i romben själv:

• S \u003d a • h \u003d a • 2r

Nedan, se exemplet med uppgiften om detta ämne.

Se fortfarande sådana artiklar om detta ämne här:

1. Rektangelns område, hur hittar man?
2. Hur hittar man ett cirkelområde?
3. Square Area - Formler.

Video: Ett exempel på hur man beräknar rombens område