Hur hittar man ett fyrkantigt område om omkretsen är känd, diagonal? Hur man hittar kvadratet på fyrkanten inskriven i cirkeln och beskrivs nära omkretsen: formel, exempel på att lösa problem. Hur hittar man sidan och diagonalen på torget, om dess område är känt?

Läs artikeln för att veta hur man hittar det fyrkantiga området på olika sätt.

Innehåll

En fyrkant är en liksidig rektangel. Denna riktiga och platta fyrkant har jämlikhet i alla sidor, hörn och diagonaler. På grund av det faktum att det finns en sådan jämlikhet är formeln för att beräkna området och andra egenskaper något modifierade jämfört med andra matematiska figurer. Men detta gör inte uppgifter för komplicerade. Låt oss analysera alla formler och lösningar på den här artikeln.

Hur hittar man sidan av torget och känner till dess område?

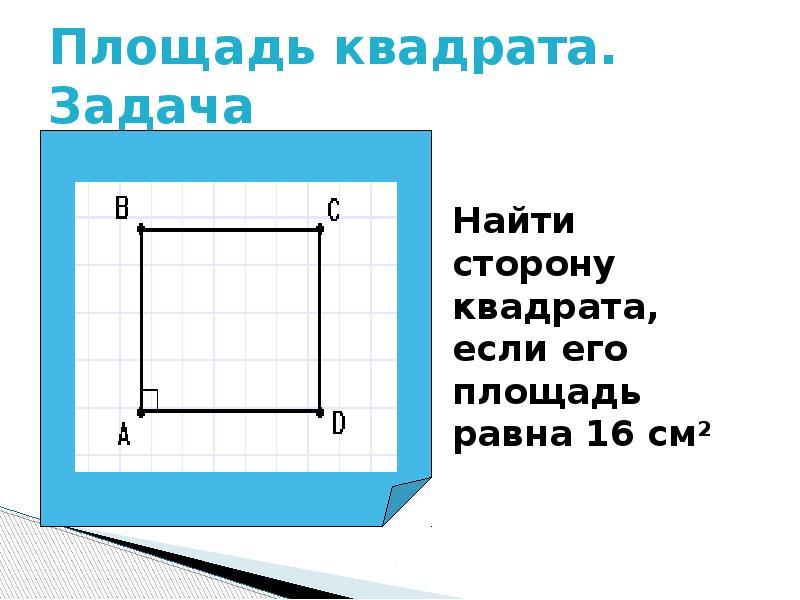
Fyrkant S. Direkta och fyrkantiga rutor beräknas med formeln: en Multiplicera med b.. Men eftersom torget har en fullständig jämlikhet mellan parterna kommer dess område att vara lika: S \u003d (a) i den andra graden.Hur man får reda på storleken på fyrkantens sida och känner till dess område?

Om det fyrkantiga fyrkantiga området är känt, hittar vi sidan genom att beräkna området under kvadratroten.
Till exempel är fyrkantens område 49, vad är sidan lika med?
49 \u003d (a) i den andra graden. Lösning: a \u003d rot på 49 \u003d 7. Svar: 7.

Om du behöver hitta sidan av torget, vars område är för långt, använd kalkylatorn. Ring först numret på området och tryck sedan på rotskylten på kalkylatortangentbordet. Det resulterande numret är svaret.

Hur hittar man en fyrkantig diagonal om dess område är känt?

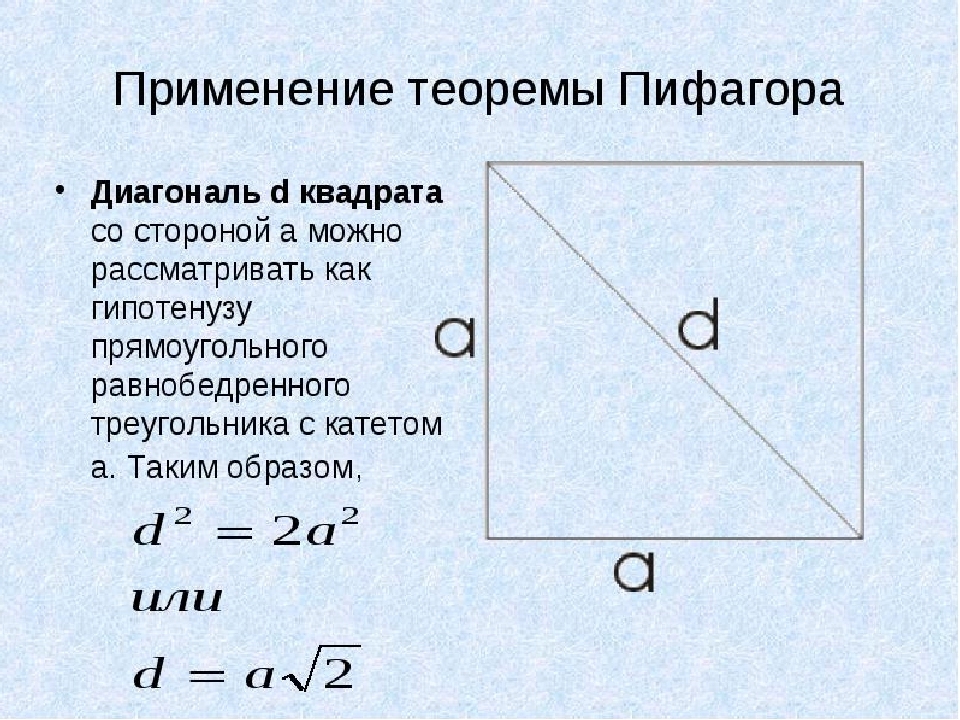
I det här exemplet kommer vi att använda Pythagoras teorem. På en fyrkant är alla sidor lika och diagonalen d. Vi kommer att överväga hypotenusen av en rektangulär likhetstriangel med ett ben en. Nu hittar vi en fyrkantig diagonal om dess område är känt:

För att inte måla hela Pythagorean Theorem kommer vi att besluta om det andra alternativet: d \u003d Aising, där A är sidan av torget.
Så vi känner till torgets område, till exempel är det lika med 64. Så en sida a \u003d √64 \u003d 8.
Det visar sig D \u003d 8√2. Roten till 2 visar sig inte hela numret, så i svaret kan du skriva på detta sätt: d \u003d 8√2. Men om du vill beräkna värdet, använd sedan räknaren: √2 \u003d 1.41421356237 och multiplicerar med 8, det visar sig 11, 3137084.

Viktig: Vanligtvis i matematik lämnas inga siffror med ett stort antal siffror som svar. Det är nödvändigt att runda eller lämna med roten. Därför är svaret på diagonalen om området är 64 enligt följande: d \u003d 8√2.

Hur hittar man ett fyrkantigt område genom en diagonal?

Formeln för att hitta det fyrkantiga området genom diagonalen är enkel:

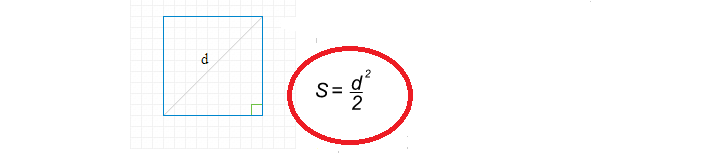
Låt oss nu skriva en lösning för att hitta det fyrkantiga området genom diagonalen:

Diagonal d \u003d 8.
8 på torget är 64.
64 Dela med 2 lika 32.
Det fyrkantiga området är 32.

Råd: Denna uppgift har en annan lösning genom Pythagoras teorem, men den är mer komplex. Använd därför den lösning som vi undersökte.

Hur hittar man ett fyrkantigt område som känner till dess omkrets?

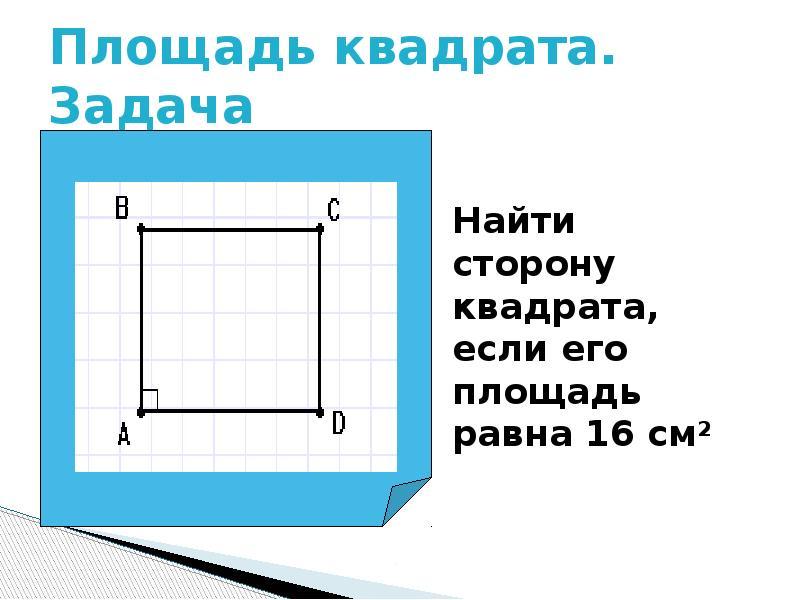
Omkretsen på fyrkanten P. - Detta är summan av alla parter. För att hitta dess område, med att känna till dess omkrets, måste du först beräkna sidan av torget. Lösning:

Anta att omkretsen är 24. Dela 24 i 4 sidor, det visar sig 6 - det här är en sida.
Nu använder vi formeln för att hitta området, veta vad sidan av torget är lika med: S \u003d a på en fyrkant, s \u003d 6 på en fyrkant \u003d 36.
Svar: 36

Som ni ser, att känna till torgets omkrets, bara hitta dess område.

Hur hittar man ett område på en fyrkantig inskriven i en cirkel med en given radie?

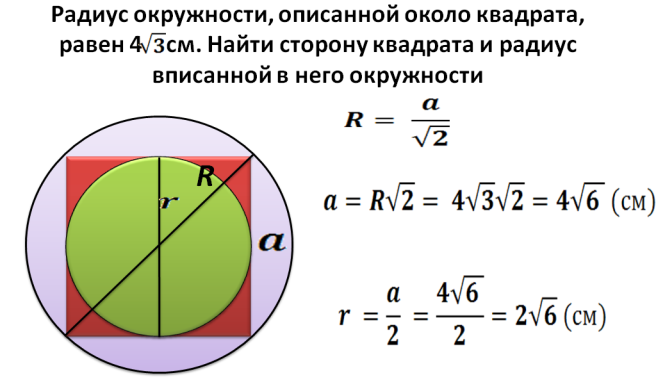
Radie R - Detta är halva diagonalen för en fyrkantig inskriven i en cirkel. Nu kan vi hitta en diagonal av formeln: d \u003d 2*r. Därefter hittar vi kvadratet på fyrkanten inskriven i en cirkel med en given radie:

Diagonalen är 2 multiplicerar med radien. Till exempel är radien 5, då är diagonalen lika 2*5=10.
Det beskrevs ovan hur man hittar torget på torget om diagonalen är känd: S \u003d diagonal i en fyrkant uppdelad i 2. S \u003d 10*10 och dela med 2 \u003d 50.
Svar - 50.

Den här uppgiften är lite mer komplicerad, men också enkelt lösas om du känner till alla formler.

Hur hittar man ett område på en fyrkant som beskrivs nära en cirkel med en given radie?

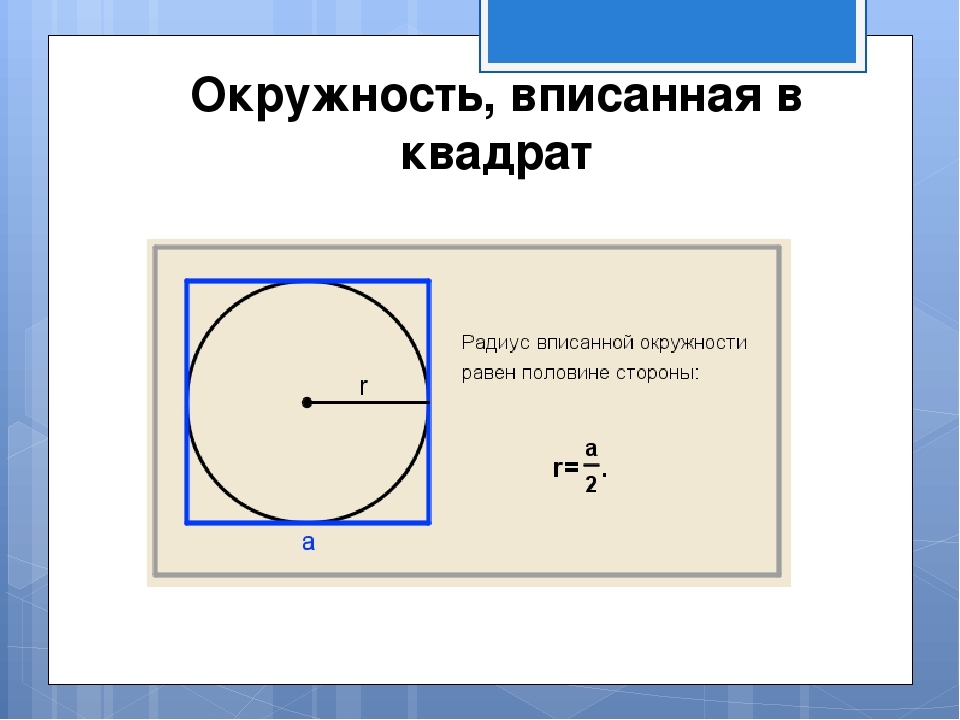
Bilden visar att radien för den inskrivna cirkeln är lika med hälften av sidan. Sidan är belägen enligt den omvända formeln som visas på bilden: a \u003d 2*r. Sedan hittar vi det fyrkant som beskrivs nära cirkeln med en given radie enligt formeln S \u003d och på en fyrkant. Lösning:

Anta att radien är 7. Sidan på kvadratet A är 2*7 \u003d 14.
S \u003d 14 på en kvadrat \u003d 196.

Om du förstår essensen att lösa sådana problem kan du lösa dem snabbt och enkelt. Låt oss titta på några fler exempel.

Exempel på att lösa problem på ämnet "Square Square"

För att fixa materialet som täcks och komma ihåg alla formler är det nödvändigt att lösa flera exempel på problem med temat "fyrkantigt område". Vi börjar med en enkel uppgift och flyttar till att lösa mer komplex: