În acest articol veți învăța cum să găsiți zona rombului cu diferite metode. Datorită acestor formule, acesta va fi rezolvat cu ușurință prin probleme de geometrie, deoarece aici articolul va descrie cum să calculeze zona rombului, știind dimensiunea diagonalei mai mari și inferioare, partea și diametrul cercului înscris în Rhombus.
Conţinut
- Cum se calculează zona rombului - proprietățile figurii
- Cum se calculează zona rombului?
- Cum să găsiți zona rombului, știind colțul și partea figurii geometrice?
- Cum se calculează zona rombului, cunoașterea diagonalelor sale?
- Cum se calculează zona rombului, cunoașterea părții sale și raza cercului înscris în el?
- VIDEO: Un exemplu despre cum să calculați zona rombului
Puteți afla zona rombului prin diferite formule. Este suficient să cunoaștem proprietățile acestei figuri și proprietățile altor figuri, deoarece rombul poate fi împărțit în triunghiuri, poate fi echivalat cu o paralelogramă etc. Mai jos veți vedea astfel de formule. De asemenea, trebuie să știți cum diferă rombul și un paralelogram. Conform definiției matematice. Rhombusul este o figură a unei astfel de paralelograme cu laturi egale, dar spre deosebire de pătrat - rombul nu are unghiuri drepte. Dar suma celor două unghiuri la baza rombului va fi de 180 de grade. Toate aceste cunoștințe vor fi la îndemână pentru calcularea zonei rombului, apoi mai detaliat.
Cum se calculează zona rombului - proprietățile figurii
Înainte de a calcula zona rombului, este mai bine să vă familiarizați cu proprietățile acestei cifre. Într -adevăr, datorită cunoașterii acestor caracteristici, va fi mai ușor să se dovedească probabilitatea unei anumite formule. Mai devreme a fost deja menționat care este Rhombus. Este o cifră cu egală cu toate părțile egale cu colțurile ascuțite opuse și mut, dar nu drept.
Rhombus are următoarele proprietăți:
- toate părțile sunt egale între ele
- colțurile care se așază unul lângă celălalt sunt, de asemenea, egale
- diagonalele acestei cifre sunt bisectoare, la punctul de intersecție sunt împărțite în segmente egale
- diagonalele se intersectează și în centrul rombului și în unghiuri drepte
- părțile opuse ale figurilor nu se pot intersecta, chiar dacă extindeți razele, acestea sunt paralele, ca o paralelogramă.
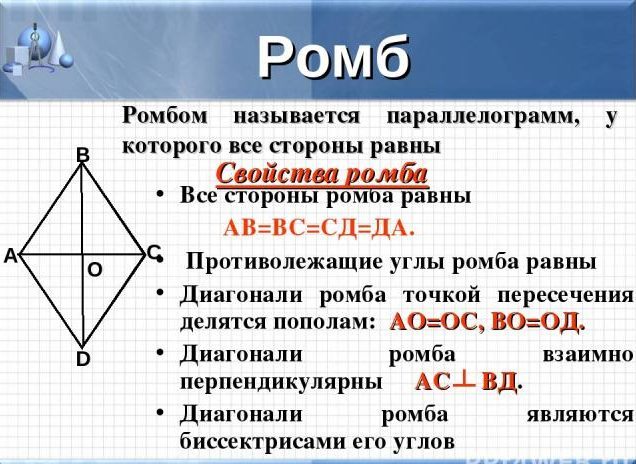
IMPORTANT: Vă rugăm să rețineți că robusul poate fi împărțit în patru triunghiuri dreptunghiulare, care vor fi egale în zonă sau prin două triunghiuri identice echilaterale, a se vedea imaginea de mai sus.
Cum se calculează zona rombului?
Deci, să aflăm cum se calculează zona rombului. Să profităm de formula pentru zona dreptunghiului, unde:
- S \u003d a • bunde A, B sunt laturile dreptunghiului.
Astfel încât să fie clar cum să eliminați formula zonei rombului din această formulă, consultați explicaţie:
- Desenați un romb, faceți o înălțime până la baza rombului BH.
- De la punctul D până la linia publicitară, desenați și o înălțime CH1.
- Se dovedește că triunghiul ABH și triunghiul CH1D sunt egali între ei pe două laturi comune, ∠ în capacul dintre ele.
- Deci ah \u003d dh1. Suprafața pătratului rezultat va fi egală cu zona rombului
- Deci, BH • HH1 - Aceasta este zona rombului, cu alte cuvinte, lucrarea rombului BH în partea AD și va fi zona S a Rhombus, deoarece HH1 \u003d BC, iar BH este cea mai mare înălţime.
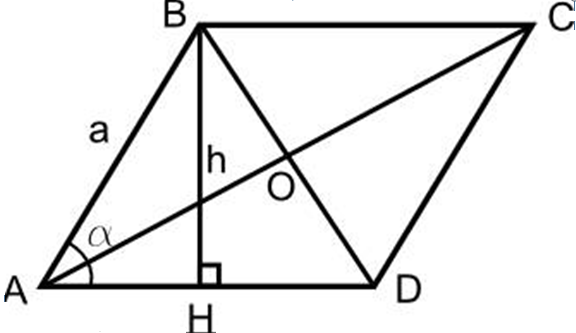
Rezultă din dovada că:
- S rombus \u003d a • h și măsurate în unități pătrate.
Cum să găsiți zona rombului, știind colțul și partea figurii geometrice?
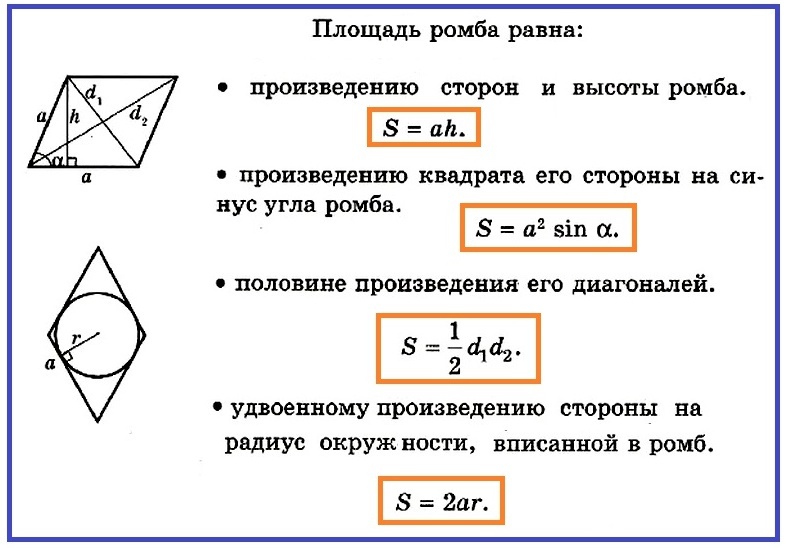
Acum știm cum arată formula zonei Rhombus, putem găsi o zonă Rhomba pe aceeași formulă, știind care este partea rombului egală cu partea rombului, de exemplu, ascuțită la bază, ca în Fotografia de mai jos.
- S \u003d a • h
Dar, în cazul nostru, nu suntem cunoscuți până la înălțimea rombului, ar trebui să se găsească. Pentru a face acest lucru, va trebui să luați în considerare un triunghi dreptunghiular, care s -a dovedit când a fost trasă înălțimea până la baza rombului.
În acest triunghi este cunoscut hipotenuză și ∠α. Pentru a calcula zona întregii cifre, va trebui să găsiți o înălțime. DAR h \u003d a • păcat. Deci, zona unei paralelograme echilaterale (rombus) este:
- S \u003d a • a • păcat ei ax \u003d a² • sinown.
Cum se calculează zona rombului, cunoașterea diagonalelor sale?
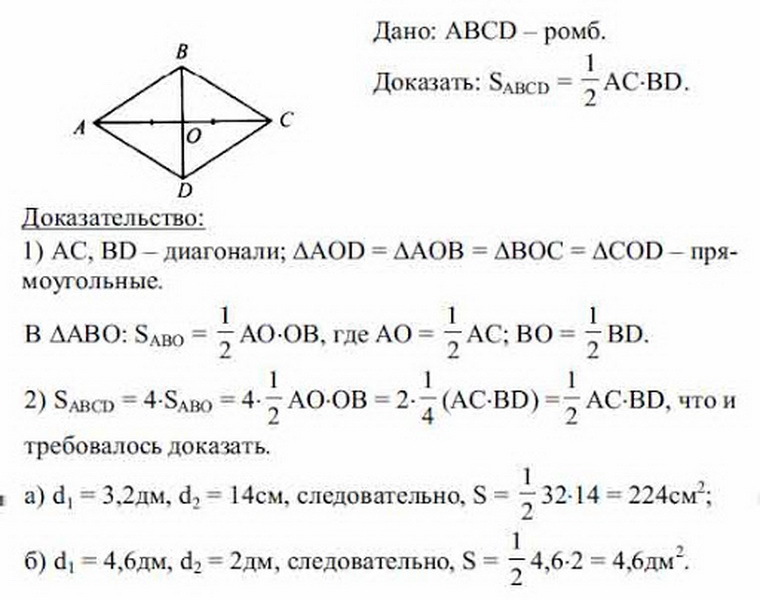
Pentru a afla formula zonei rombului, atunci când sunt cunoscute doar diagonale (a, b), trebuie luat în considerare următorul exemplu. BCDA este dat - Rhombus și știți ce diagonale sunt egale. Acum este necesar să găsiți zona unei paralelograme echilaterale în ceea ce privește diagonalele.
Anterior, proprietățile rombului erau deja luate în considerare. Diagonalele rombului sunt egale, la punctul de intersecție sunt împărțite în segmente egale. Din aceasta rezultă că toate triunghiurile care sunt înscrise în figură ca urmare a intersecției ambelor diagonale sunt, de asemenea, egale între ele și sunt dreptunghiulare (pe trei laturi). Pentru a găsi zona rombului, este suficient să găsiți zona unui triunghi și să înmulțiți datele obținute cu 4.
În total, se dovedește că:
- S rombus \u003d 4 (1/2 ao • ob + 1/2 bo • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Total pătrat s Romm va fi \u003d munca a • b (diagonale) împărțite la două: S \u003d 1/2 A • B
Cum se calculează zona rombului, cunoașterea părții sale și raza cercului înscris în el?
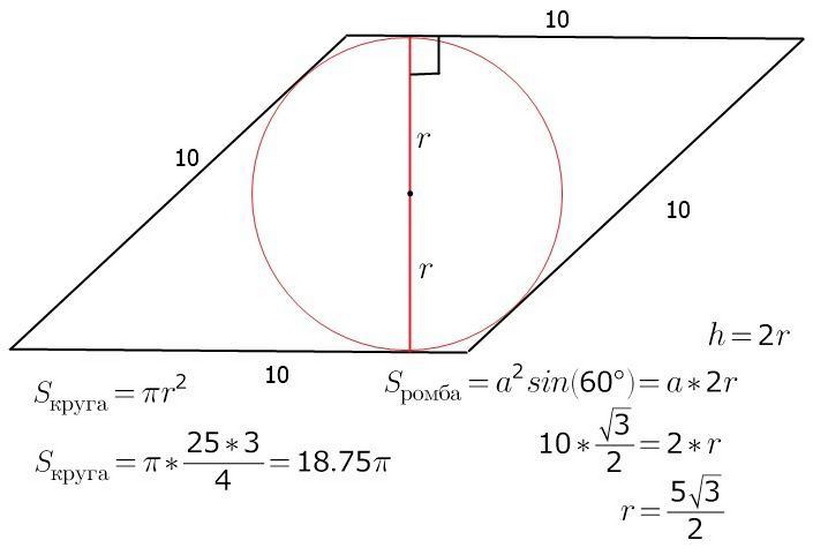
Zona rombului poate fi calculată prin cunoașterea R - raza și A - lungimea laterală a figurii. Se știe deja că s - zona figurii va fi egală cu munca b - partea de pe înălțimea H. Prin centrul cercului, acesta va fi și centrul de intersecție A, B este diagonalele rombului. Efectuați înălțimea și, în același timp, diametrul rombului. Imaginea arată că înălțimea figurii este de două raze ale cercului. Acum va fi ușor să găsiți zona rombului în sine:
- S \u003d a • h \u003d a • 2r
Mai jos, consultați exemplul sarcinii pe acest subiect.
Vedeți în continuare astfel de articole pe acest subiect aici:







