Cum să găsiți o suprafață pătrată dacă perimetrul este cunoscut, diagonală? Cum se găsește pătratul pătratului înscris în cerc și descris în apropierea circumferinței: formula, exemple de rezolvare a problemelor. Cum să găsești partea și diagonația pătratului, dacă zona sa este cunoscută?

Citiți articolul pentru a ști cum să găsiți suprafața pătrată în moduri diferite.

Conţinut

Un pătrat este un dreptunghi echilateral. Acest cvadrangle adecvat și plat are egalitate în toate părțile, colțurile și diagonalele. Datorită faptului că există o astfel de egalitate, formula pentru calcularea zonei și a altor caracteristici este ușor modificată în comparație cu alte figuri matematice. Dar acest lucru nu face ca sarcinile să fie prea complicate. Să analizăm toate formulele și soluțiile la acest articol.

Cum să găsești partea pătratului, cunoașterea zonei sale?

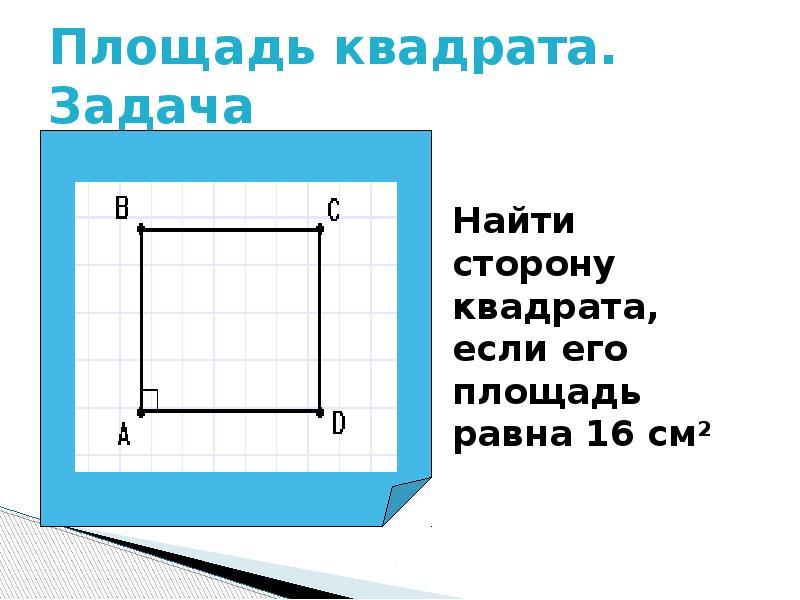
Pătrat S. Pătratele directe și pătrate sunt calculate după formula: A Înmulțit cu b.. Dar, deoarece piața are o egalitate completă a părților, zona sa va fi egală: S \u003d (a) în gradul doi.Cum să aflați dimensiunea părții pătratului, cunoașterea zonei sale?

Dacă este cunoscută suprafața pătratului pătrat, atunci găsim partea calculând zona de sub rădăcina pătrată.
De exemplu, zona pătratului este 49, atunci care este partea egală cu?
49 \u003d (a) în gradul doi. Soluţie: a \u003d rădăcina de 49 \u003d 7. Răspuns: 7.

Dacă trebuie să găsiți partea pătratului pătrat, a cărei suprafață este prea lungă, atunci utilizați calculatorul. Mai întâi formați numărul zonei, apoi apăsați semnul rădăcină de pe tastatura calculatorului. Numărul rezultat va fi răspunsul.

Cum să găsești o diagonală pătrată dacă zona sa este cunoscută?

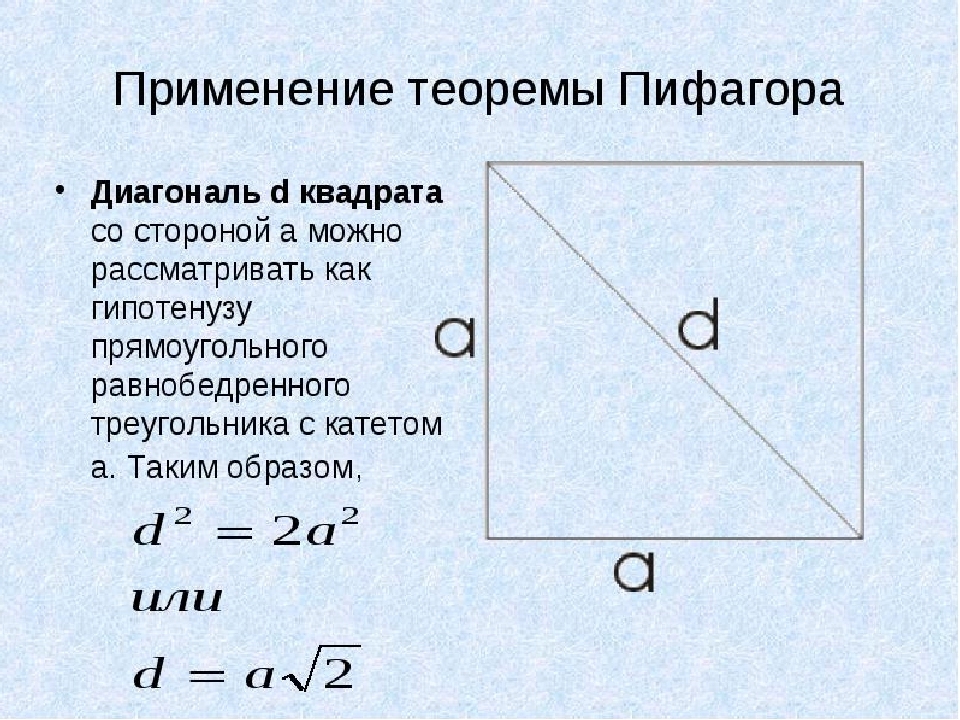
În acest exemplu, vom folosi teorema Pitagoras. Într -un pătrat, toate părțile sunt egale, iar diagonală d. Vom considera o hipotenuză a unui triunghi dreptunghiular izoscel cu un picior a. Acum găsim o diagonală pătrată dacă zona sa este cunoscută:

Pentru a nu picta întreaga teoremă pitagoreană, vom decide cu privire la a doua opțiune: d \u003d aising, unde a este partea pătratului.
Deci, știm zona pătratului, de exemplu, este egală cu 64. Deci, o parte a \u003d √64 \u003d 8.
Se dovedește D \u003d 8√2. Rădăcina de 2 nu dovedește întregul număr, așa că în răspuns puteți scrie în acest fel: d \u003d 8√2. Dar, dacă doriți să calculați valoarea, utilizați calculatorul: √2 \u003d 1.41421356237 și înmulțiți cu 8, se dovedește 11, 3137084.

Important: În mod obișnuit, în matematică, nu există un număr mare de numere ca răspuns. Este necesar să rotunjiți sau să plecați cu rădăcina. Prin urmare, răspunsul la diagonală este dacă zona este 64 după cum urmează: d \u003d 8√2.

Cum să găsiți o suprafață pătrată printr -o diagonală?

Formula pentru găsirea zonei pătrate prin diagonală este simplă:

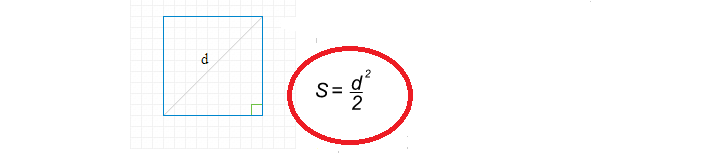
Acum să scriem o soluție pentru a găsi zona pătrată prin diagonală:

Diagonala D \u003d 8.
8 în pătrat este de 64.
64 Împărțiți cu 2 egal 32.
Suprafața pătrată este de 32.

Sfat: Această sarcină are o altă soluție prin teorema Pitagoras, dar este mai complexă. Prin urmare, utilizați soluția pe care am examinat -o.

Cum să găsești o suprafață pătrată, știind perimetrul acesteia?

Perimetrul pătratului pătrat P. - Aceasta este suma tuturor părților. Pentru a -și găsi zona, cunoașterea perimetrului său, trebuie să calculați mai întâi partea pătratului pătrat. Soluţie:

Să presupunem că perimetrul este 24. Împărțiți 24 în 4 laturi, se dovedește 6 - aceasta este o parte.
Acum folosim formula pentru a găsi zona, știind care este partea pătratului pătrat este egală cu: S \u003d a într -un pătrat, s \u003d 6 într -un pătrat \u003d 36.
Răspuns: 36

După cum puteți vedea, cunoașterea perimetrului pătratului, găsiți doar zona sa.

Cum să găsiți o zonă a unui pătrat înscris într -un cerc cu o rază dată?

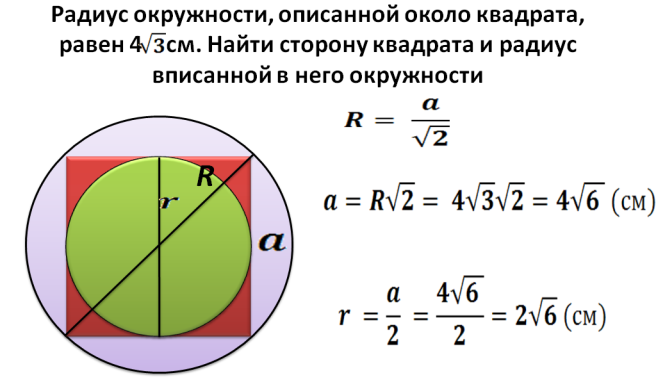
Rază R - Aceasta este jumătate din diagonală a unui pătrat înscris într -un cerc. Acum putem găsi o diagonală după formula: d \u003d 2*r. În continuare, găsim pătratul pătratului înscris într -un cerc cu o rază dată:

Diagonala este înmulțită cu 2 cu raza. De exemplu, raza este 5, atunci diagonația este egală 2*5=10.
A fost descris mai sus cum să găsiți pătratul pătratului dacă se cunoaște diagonală: S \u003d diagonală într -un pătrat împărțit în 2. s \u003d 10*10 și împărțiți cu 2 \u003d 50.
Răspuns - 50.

Această sarcină este puțin mai complicată, dar și ușor de rezolvat dacă cunoașteți toate formulele.

Cum să găsiți o zonă a unui pătrat descris în apropierea unui cerc cu o rază dată?

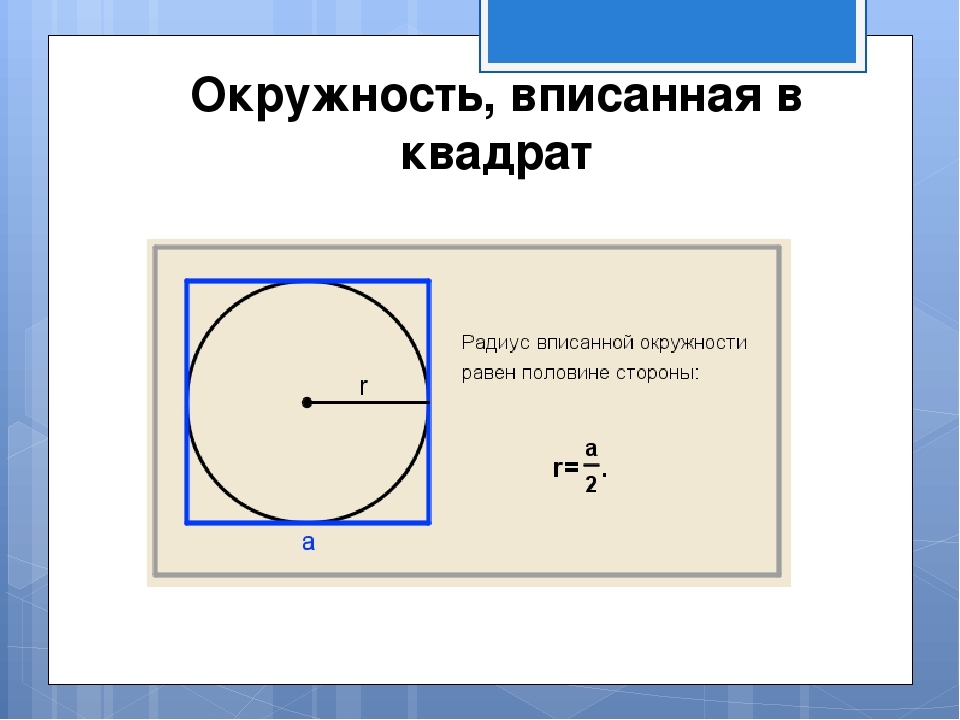
Imaginea arată că raza cercului înscris este egală cu jumătate din partea laterală. Partea este situată conform formulei inversă care a fost descrisă în imagine: a \u003d 2*r. Apoi găsim zona pătratului descrisă în apropierea cercului cu o rază dată în conformitate cu formula S \u003d și într -un pătrat. Soluţie:

Să presupunem că raza este 7. latura pătratului A este 2*7 \u003d 14.
S \u003d 14 într -un pătrat \u003d 196.

Dacă înțelegeți esența rezolvării unor astfel de probleme, atunci le puteți rezolva rapid și pur și simplu. Să ne uităm la alte câteva exemple.

Exemple de rezolvare a problemelor pe subiectul „pătrat pătrat”

Pentru a remedia materialul acoperit și a aminti toate formulele, este necesar să se rezolve mai multe exemple de probleme pe tema „Zona pătrată”. Începem cu o sarcină simplă și trecem la rezolvarea mai complexă: