როგორ გამოვთვალოთ Rhombus- ის ფართობი?

ამ სტატიაში თქვენ შეისწავლით თუ როგორ უნდა იპოვოთ Rhombus- ის ტერიტორია სხვადასხვა მეთოდით. ამ ფორმულების წყალობით, იგი ადვილად მოგვარდება გეომეტრიის პრობლემებით, რადგან აქ სტატიაში აღწერილია თუ როგორ უნდა გამოთვალოთ რომბუსის ფართობი, იცოდეს დიაგონალის ზომა უფრო დიდი და პატარა, მხარის, კუთხეების და დიამეტრის დიაგონალზე წარწერა წრე Rhombus- ში.

თქვენ შეგიძლიათ გაიგოთ Rhombus- ის ფართობი სხვადასხვა ფორმულებით. საკმარისია იცოდეთ ამ ფიგურის თვისებები და სხვა ფიგურების თვისებები, რადგან Rhombus შეიძლება დაიყოს სამკუთხედებად, ის შეიძლება თანაბარი იყოს პარალელოგრამით და ა.შ. ქვემოთ ნახავთ ასეთ ფორმულებს. თქვენ ასევე უნდა იცოდეთ, როგორ განსხვავდება Rhombus და პარალელოგრამა. მათემატიკური განმარტებით. Rhombus არის ასეთი პარალელოგრამის ფიგურა თანაბარი მხარეებით, მაგრამ კვადრატისგან განსხვავებით - Rhombus- ს არ აქვს სწორი კუთხეები. მაგრამ Rhombus– ის ბაზაზე ორი კუთხის ჯამი იქნება 180 გრადუსი. მთელი ეს ცოდნა მოსახერხებელია რომბუსის ფართობის გამოანგარიშებისთვის, შემდეგ უფრო დეტალურად.

როგორ გამოვთვალოთ რომბუსის ფართობი - ფიგურის თვისებები

Rhombus– ის ფართობის გაანგარიშებამდე, უმჯობესია გაეცნოთ ამ ფიგურის თვისებებს. მართლაც, ამ მახასიათებლების ცოდნის წყალობით, უფრო ადვილი იქნება კონკრეტული ფორმულის ალბათობის დამტკიცება. ადრე უკვე აღინიშნა რა არის Rhombus. ეს არის ფიგურა, რომელსაც ტოლია ყველა მხრიდან, საპირისპირო მკვეთრი და მუნჯი კუთხეების ტოლია, მაგრამ არა სწორი.

Rhombus– ს აქვს შემდეგი თვისებები:

• ყველა მხარე ერთმანეთის ტოლია
• კუთხეები, რომლებიც ერთმანეთის საპირისპიროდ იწევს, ასევე თანაბარია
• ამ ფიგურის დიაგონალები არის ბისექტორები, კვეთაზე წერტილში იყოფა თანაბარ სეგმენტებად
• დიაგონალები ასევე კვეთენ Rhombus- ის ცენტრში და მარჯვენა კუთხეებით
• ფიგურების საპირისპირო მხარეები ვერ გადაკვეთენ, მაშინაც კი, თუ სხივებს გააფართოვებთ, ისინი პარალელურია, პარალელოგრამის მსგავსად.

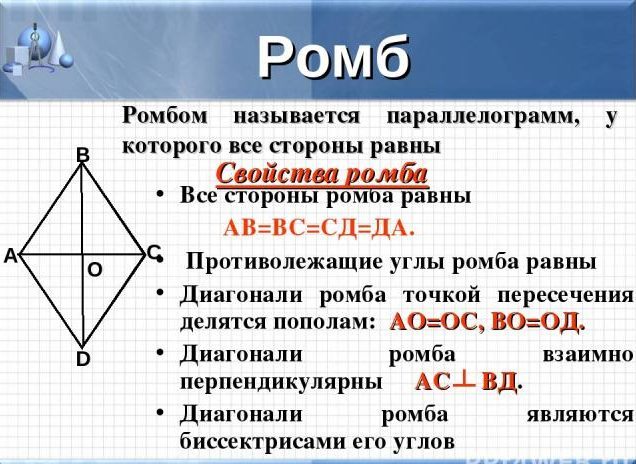
ᲛᲜᲘᲨᲕᲜᲔᲚᲝᲕᲐᲜᲘ: გთხოვთ გაითვალისწინოთ, რომ Rhombus შეიძლება დაიყოს ოთხ მართკუთხა სამკუთხედად, რომლებიც თანაბარი იქნება ფართობში, ან ორი თანაბარი იდენტური სამკუთხედით, იხილეთ ზემოთ მოცემული სურათი.

როგორ გამოვთვალოთ Rhombus- ის ფართობი?

მოდით გავარკვიოთ, თუ როგორ გამოითვლება Rhombus- ის არეალი. მოდით ვისარგებლოთ მართკუთხედის არეალის ფორმულით, სადაც:

• S \u003d a • bსადაც a, b არის მართკუთხედის მხარეები.

იმის გასაგებად, თუ როგორ უნდა მიიღოთ Rhombus ფორმულა ამ ფორმულიდან, ტერიტორიის ფორმულა, იხილეთ განმარტება:

1. დახაზეთ რომბუსი, გააკეთეთ სიმაღლე BH Rhombus- ის ბაზაზე.
2. D წერტილიდან სარეკლამო ხაზამდე, ასევე მიაპყროს CH1 სიმაღლე.
3. გამოდის, რომ სამკუთხედი ABH და სამკუთხედი CH1D ერთმანეთთან ტოლია ორ საერთო მხრიდან, ∠ საფარი მათ შორის.
4. ასე რომ, აჰ \u003d dh1. შედეგად მიღებული კვადრატის ფართობი ტოლი იქნება Rhombus- ის ფართობზე
5. ასე რომ, BH • HH1 არის Rhombus– ის ფართობი, სხვა სიტყვებით რომ ვთქვათ, BH Romb სიმაღლეზე მუშაობა AD– ის მხარეს და იქნება Rombus– ის სფერო, რადგან HH1 \u003d BC, და BH არის სიმაღლე .

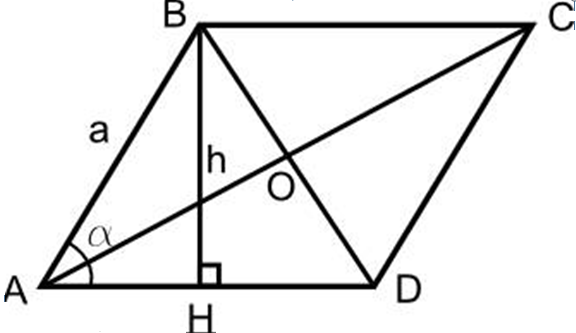
ეს გამომდინარეობს იმის მტკიცებით, რომ:

• S rhombus \u003d a • H და იზომება კვადრატულ ერთეულებში.

როგორ მოვიძიოთ ROMB- ის ფართობი, ვიცოდეთ გეომეტრიული ფიგურის კუთხე და მხარე?

ახლა ჩვენ ვიცით, როგორ გამოიყურება Rhombus- ის არეალის ფორმულა, ჩვენ შეგვიძლია ვიპოვოთ Rhomba- ს ფართ ქვემოთ მოცემული ფოტო.

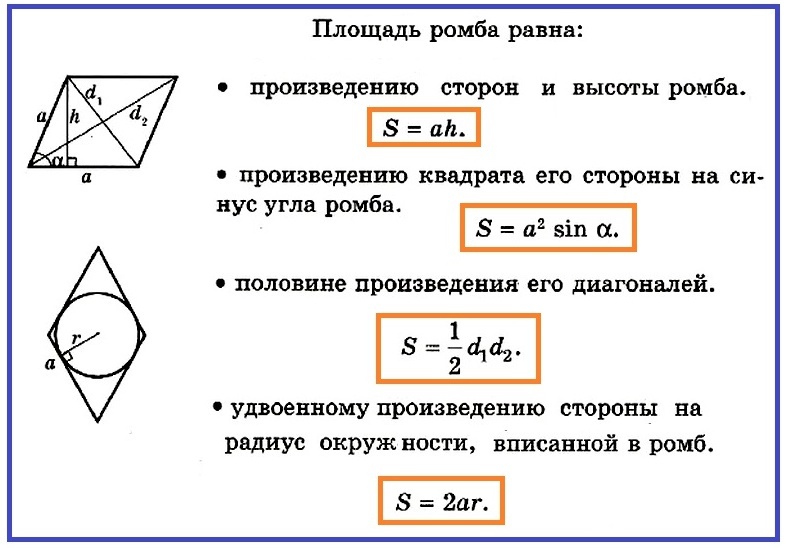
• S \u003d a • H

მაგრამ ჩვენს შემთხვევაში, ჩვენ უცნობია Rhombus- ის სიმაღლეზე, ის უნდა იპოვოთ. ამისათვის თქვენ უნდა გაითვალისწინოთ მართკუთხა სამკუთხედი, რომელიც აღმოჩნდა, როდესაც სიმაღლე მიაპყრო რომბუსის ფუძეს.

ამ სამკუთხედში ცნობილია ჰიპოტენეზა და ∠α. მთელი ფიგურის ფართობის გამოსათვლელად, თქვენ უნდა იპოვოთ სიმაღლე. განუსაზღვრელი არტიკლი h \u003d a • ცოდვა. ასე რომ, თანაბარი პარალელოგრამის (Rhombus) ფართობი არის:

• S \u003d a • a • ცოდვა ისინი AX \u003d a² • ცოდვა.

როგორ გამოვთვალოთ Rhombus- ის ფართობი, მისი დიაგონალების ცოდნა?

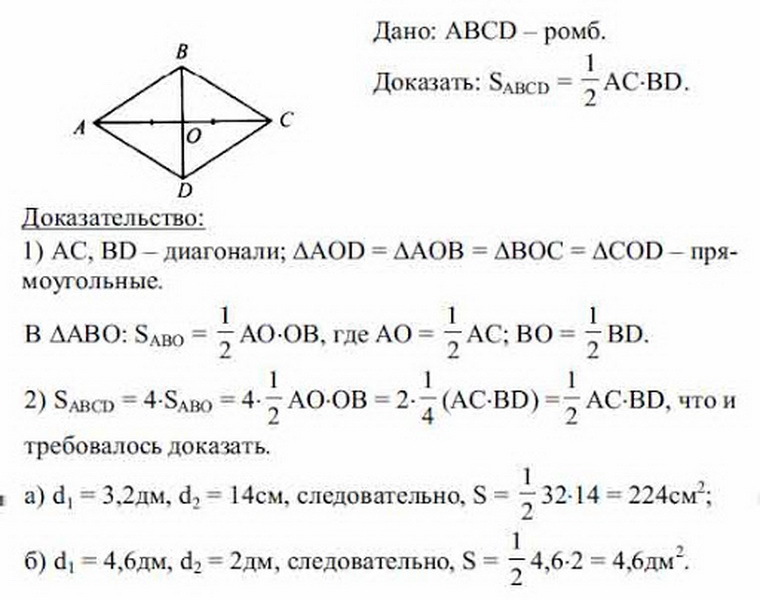
Rhombus- ის ფართობის ფორმულის გასარკვევად, როდესაც ცნობილია მხოლოდ (ა, ბ) დიაგონალები, უნდა განიხილებოდეს შემდეგი მაგალითი. BCDA ეძლევა - Rhombus და იცოდეთ რა დიაგონალები თანაბარია. ახლა აუცილებელია დიაგონალების თვალსაზრისით თანაბარი პარალელოგრამის ფართობი.

ადრე, Rhombus- ის თვისებები უკვე განიხილებოდა. Rhombus- ის დიაგონალები თანაბარია, კვეთა წერტილში ისინი თანაბარ სეგმენტებად იყოფა. აქედან გამომდინარეობს, რომ ყველა სამკუთხედი, რომელიც მოცემულია ფიგურაში, ორივე დიაგონალის კვეთა, ასევე ტოლია ერთმანეთთან და ისინი მართკუთხა არიან (სამი მხრიდან). Rhombus- ის ფართობის მოსაძებნად, საკმარისია იპოვოთ ერთი სამკუთხედის ფართობი და გაამრავლოთ 4 -ით მოპოვებული მონაცემები.

საერთო ჯამში, გამოდის:

• S Rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC,, მთლიანი კვადრატული s romm იქნება \u003d სამუშაო A • B (დიაგონალები) დაყოფილია ორით: S \u003d 1/2 A • B

როგორ გამოვთვალოთ რომბუსის ფართობი, იცოდეთ მისი მხარე და მასში ჩაწერილი წრის რადიუსი?

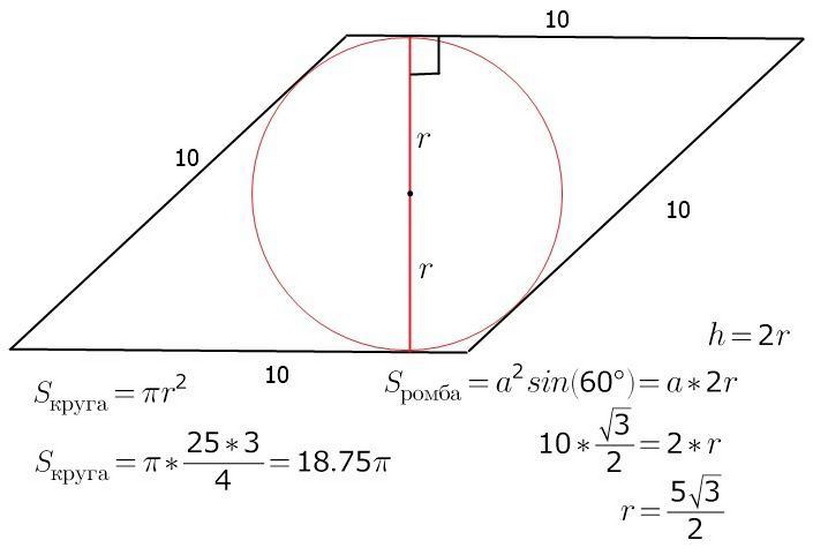
Rhomba- ს არეალი შეიძლება გამოითვალოს ფიგურის მხარის სიგრძის ცოდნით. უკვე ცნობილია, რომ S - ფიგურის ფართობი ტოლი იქნება სამუშაო B - მხარე H - სიმაღლეზე. წრის ცენტრის მეშვეობით, ეს იქნება ასევე კვეთა ცენტრი A, B არის Rhombus- ის დიაგონალები. განახორციელეთ სიმაღლე და ამავე დროს, რომბუსის დიამეტრი. სურათი გვიჩვენებს, რომ ფიგურის სიმაღლე არის წრის ორი რადიუსი. ახლა ადვილი იქნება თავად Rhombus- ის ფართობის პოვნა:

• S \u003d a • h \u003d a • 2r

ქვემოთ მოცემულია ამოცანის დავალების მაგალითი.

კვლავ ნახეთ ასეთი სტატიები ამ თემასთან დაკავშირებით:

1. მართკუთხედის ფართობი, როგორ მოვიძიოთ?
2. როგორ მოვძებნოთ წრის არეალი?
3. კვადრატული ფართობი - ფორმულები.

ვიდეო: მაგალითი იმისა, თუ როგორ უნდა გამოვთვალოთ რომბუსის არეალი