როგორ მოვიძიოთ კვადრატული ფართობი, თუ ცნობილია პერიმეტრი, დიაგონალი? როგორ მოვიძიოთ წრეში ჩაწერილი კვადრატული კვადრატი და აღწერილი წრეწირის მახლობლად: ფორმულა, პრობლემების გადაჭრის მაგალითები. როგორ მოვიძიოთ კვადრატის მხარე და დიაგონალი, თუ მისი ტერიტორია ცნობილია?

წაიკითხეთ სტატია, რომ იცოდეთ როგორ იპოვოთ კვადრატული ფართობი სხვადასხვა გზით.

კმაყოფილი

კვადრატი არის თანაბარი ოთხკუთხედი. ამ სათანადო და ბრტყელ ოთხკუთხედს აქვს თანასწორობა ყველა მხრიდან, კუთხეებში და დიაგონალში. გამომდინარე იქიდან, რომ არსებობს ასეთი თანასწორობა, ფართობის და სხვა მახასიათებლების გამოანგარიშების ფორმულა ოდნავ შეცვლილია სხვა მათემატიკური ფიგურებთან შედარებით. მაგრამ ეს არ ქმნის დავალებებს ძალიან რთულდება. მოდით გავაანალიზოთ ამ სტატიის ყველა ფორმულა და გადაწყვეტილება.

როგორ მოვძებნოთ მოედნის მხარე, ვიცოდეთ მისი ტერიტორია?

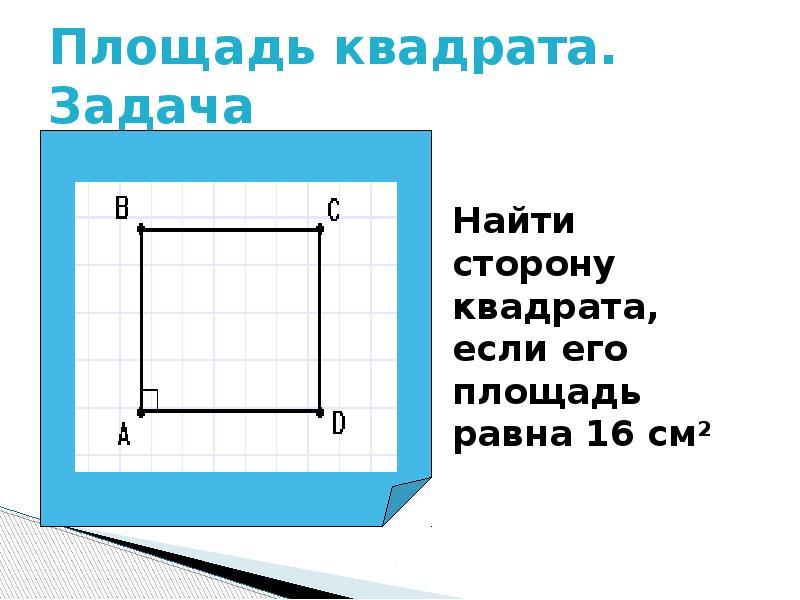
კვადრატი S. პირდაპირი და კვადრატული მოედნები გამოითვლება ფორმულით: განუსაზღვრელი არტიკლი გამრავლება ბ.. რადგან მოედანს აქვს მხარეთა სრული თანასწორობა, მისი ტერიტორია თანაბარი იქნება: S \u003d (ა) მეორე ხარისხში.როგორ გავარკვიოთ კვადრატის მხარის ზომა, მისი არეალის ცოდნა?

თუ ცნობილია კვადრატული კვადრატის ფართობი, მაშინ ჩვენ ვპოულობთ მხარეს კვადრატული ფესვიდან ფართობის გამოანგარიშებით.
მაგალითად, კვადრატის ფართობი 49, მაშინ რა არის მხარე ტოლი?
49 \u003d (ა) მეორე ხარისხში. გამოსავალი: a \u003d ფესვი 49 \u003d 7. პასუხი: 7.

თუ თქვენ უნდა იპოვოთ კვადრატული მოედნის მხარე, რომლის ფართობი ძალიან გრძელია, მაშინ გამოიყენეთ კალკულატორი. ჯერ აკრიფეთ ფართობის რაოდენობა, შემდეგ კი დააჭირეთ ფესვის ნიშანს კალკულატორის კლავიატურაზე. შედეგად მიღებული ნომერი იქნება პასუხი.

როგორ მოვიძიოთ კვადრატული დიაგონალი, თუ მისი ტერიტორია ცნობილია?

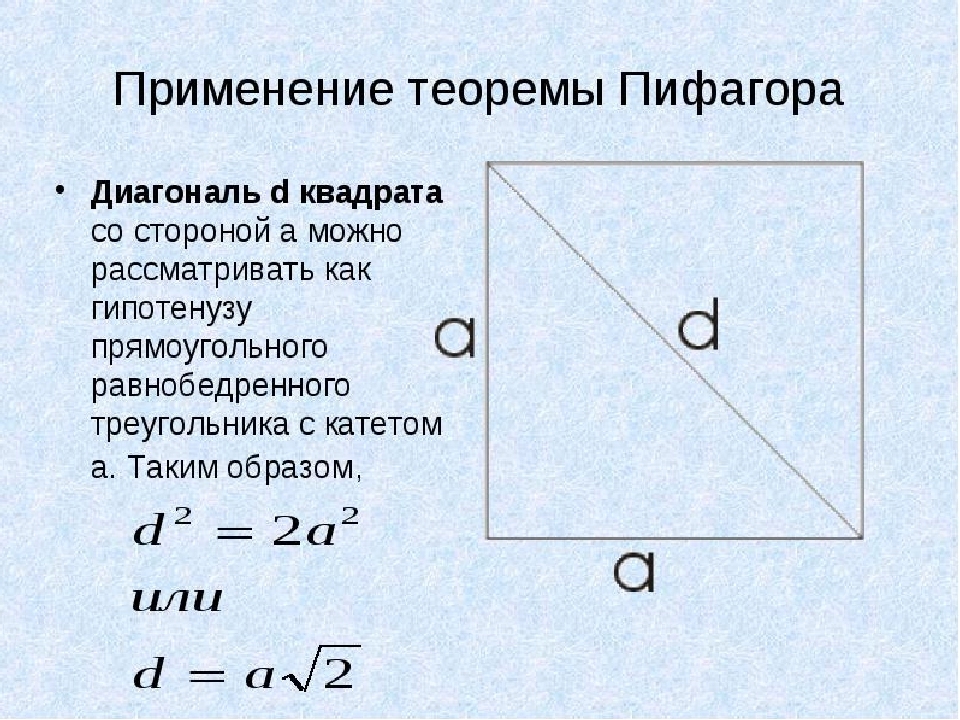
ამ მაგალითში ჩვენ გამოვიყენებთ პითაგორას თეორემას. კვადრატში, ყველა მხარე თანაბარია, ხოლო დიაგონალი დ. ჩვენ განვიხილავთ, როგორც მართკუთხა იზოსკების სამკუთხედის ჰიპოტენუსს ფეხი განუსაზღვრელი არტიკლი. ახლა ჩვენ ვხვდებით კვადრატულ დიაგონალს, თუ მისი ტერიტორია ცნობილია:

იმისათვის, რომ არ დავხატოთ მთელი პითაგორული თეორემა, ჩვენ გადავწყვეტთ მეორე ვარიანტს: d \u003d aising, სადაც a არის მოედნის მხარე.
ასე რომ, ჩვენ ვიცით მოედნის ფართობი, მაგალითად, ის ტოლია 64. ასე რომ, ერთი მხარე a \u003d √64 \u003d 8.
გამოდის D \u003d 8√2. 2 -ის ფესვი არ გამოდგება მთელ რიცხვზე, ასე რომ, პასუხში შეგიძლიათ დაწეროთ ეს გზა: d \u003d 8√2. მაგრამ, თუ გსურთ გამოთვალოთ მნიშვნელობა, გამოიყენეთ კალკულატორი: √2 \u003d 1.41421356237 და მრავლდება 8 -ით, გამოდის 11, 3137084.

Მნიშვნელოვანი: როგორც წესი, მათემატიკაში, დიდი რაოდენობით რიცხვები არ დარჩა საპასუხოდ. აუცილებელია ფესვებით მრგვალი ან დატოვება. აქედან გამომდინარე, დიაგონალზე პასუხი არის თუ ფართობი 64 შემდეგნაირია: d \u003d 8√2.

როგორ მოვძებნოთ კვადრატული ფართობი დიაგონალში?

დიაგონალის მეშვეობით კვადრატული ფართობის მოსაძებნად ფორმულა მარტივია:

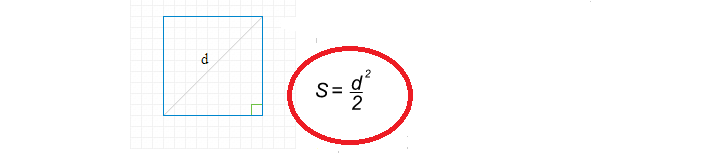
ახლა მოდით დავწეროთ გამოსავალი, რომ იპოვოთ კვადრატული ფართობი დიაგონალის მეშვეობით:

დიაგონალი D \u003d 8.
8 მოედანზე არის 64.
64 გაყავით 2 თანაბარი 32.
კვადრატული ფართობი არის 32.

რჩევა: ამ ამოცანას კიდევ ერთი გამოსავალი აქვს პითაგორას თეორემის მეშვეობით, მაგრამ ის უფრო რთულია. ამიტომ, გამოიყენეთ გამოსავალი, რომელიც ჩვენ გამოვიკვლიეთ.

როგორ მოვძებნოთ კვადრატული ფართობი, ვიცით მისი პერიმეტრი?

კვადრატული კვადრატის პერიმეტრი გვ. - ეს არის ყველა მხარის ჯამი. მისი ტერიტორიის მოსაძებნად, მისი პერიმეტრის ცოდნის მისაღებად, ჯერ უნდა გამოთვალოთ კვადრატული კვადრატის მხარე. გამოსავალი:

დავუშვათ, რომ პერიმეტრია 24. გაყავით 24 4 მხარეს, გამოდის 6 - ეს არის ერთი მხარე.
ახლა ჩვენ ვიყენებთ ფორმულას ტერიტორიის მოსაძებნად, ვიცით, რა არის კვადრატული მოედნის მხარე ტოლი: S \u003d a კვადრატში, s \u003d 6 კვადრატში \u003d 36.
პასუხი: 36

როგორც ხედავთ, კვადრატის პერიმეტრის ცოდნის შესახებ, უბრალოდ იპოვნეთ მისი ტერიტორია.

როგორ მოვიძიოთ კვადრატული ფართობი, რომელიც მოცემულია წრეში მოცემული რადიუსით?

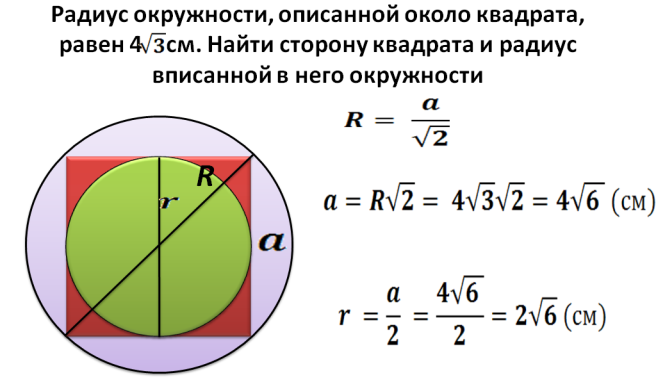
რადიუსი R - ეს არის წრეში ჩაწერილი კვადრატის ნახევარი დიაგონალი. ახლა ჩვენ შეგვიძლია ვიპოვოთ დიაგონალი ფორმულით: d \u003d 2*r. შემდეგი, ჩვენ ვიპოვით კვადრატის კვადრატს, რომელიც მოცემულია წრეში მოცემული რადიუსით:

დიაგონალი 2 მრავლდება რადიუსის მიერ. მაგალითად, რადიუსი არის 5, მაშინ დიაგონალი თანაბარია 2*5=10.
ზემოთ იყო აღწერილი, თუ როგორ უნდა იპოვოთ კვადრატის კვადრატი, თუ დიაგონალი ცნობილია: S \u003d დიაგონალი კვადრატში დაყოფილია 2. s \u003d 10*10 და გაყავით 2 \u003d 50.
პასუხი - 50.

ეს ამოცანა ცოტა უფრო რთულია, მაგრამ ასევე ადვილად მოგვარებულია, თუ იცით ყველა ფორმულა.

როგორ მოვიძიოთ კვადრატის ფართობი, რომელიც აღწერილია წრის მახლობლად მოცემული რადიუსით?

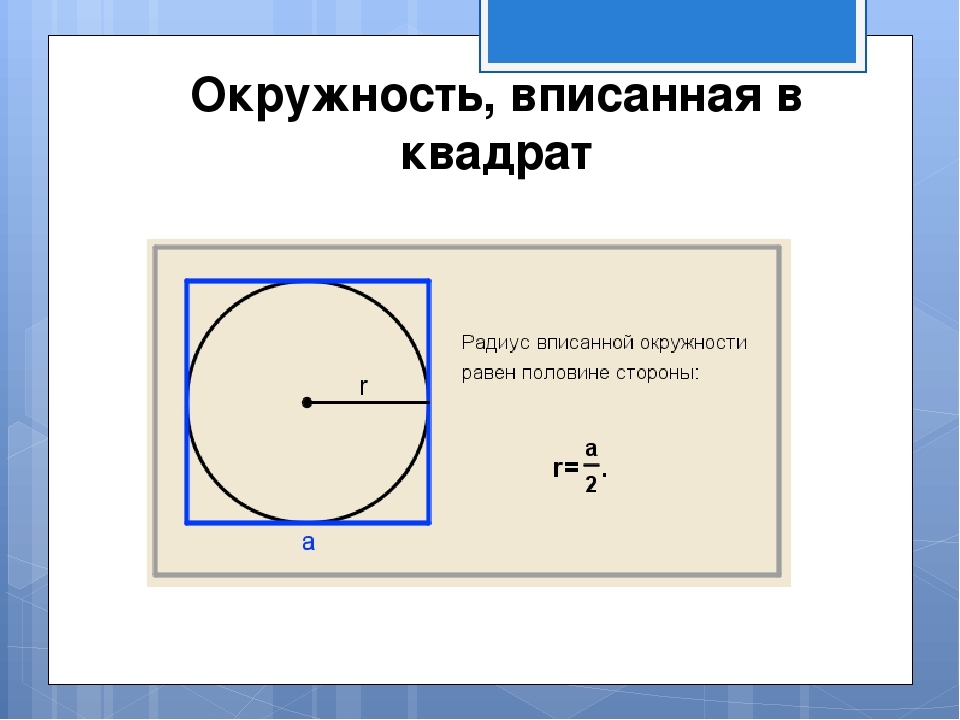
სურათი გვიჩვენებს, რომ წარწერის წრის რადიუსი ტოლია მხარის ნახევარზე. მხარე მდებარეობს საპირისპირო ფორმულის მიხედვით, რომელიც გამოსახულია სურათზე: a \u003d 2*r. შემდეგ ჩვენ ვხვდებით წრის მახლობლად აღწერილი კვადრატის ფართს, რომელზეც მოცემული რადიუსი ფორმულის მიხედვით S \u003d და მოედანზე. გამოსავალი:

დავუშვათ, რომ რადიუსი არის 7. კვადრატის A მხარეს არის 2*7 \u003d 14.
S \u003d 14 კვადრატში \u003d 196.

თუ გესმით ასეთი პრობლემების გადაჭრის არსი, მაშინ შეგიძლიათ სწრაფად და მარტივად მოაგვაროთ ისინი. მოდით გადავხედოთ კიდევ რამდენიმე მაგალითს.

პრობლემების გადაჭრის მაგალითები თემაზე "კვადრატული მოედანი"

დაფარული მასალის დასადგენად და ყველა ფორმულის დასამახსოვრებლად, აუცილებელია პრობლემების რამდენიმე მაგალითის მოგვარება "კვადრატული ფართობის" თემაზე. ჩვენ ვიწყებთ მარტივი დავალებით და გადავდივართ უფრო რთული:

კვადრატული ფართობის თემატიკაზე პრობლემების გადაჭრის მაგალითები

რთული პრობლემების გადაჭრის მაგალითები თემაზე "კვადრატული მოედანი"

ახლა თქვენ იცით, თუ როგორ გამოიყენოთ ფორმულა კვადრატის კვადრატისთვის, რაც იმას ნიშნავს, რომ შეგიძლიათ ნებისმიერი დავალების შესრულება. წარმატება მომავალ ტრენინგში!