چگونه می توان مساحت رومبوس را محاسبه کرد؟

در این مقاله یاد خواهید گرفت که چگونه می توانید منطقه رومبوس را با روش های مختلف پیدا کنید. به لطف این فرمول ها ، به راحتی با مشکلات هندسه حل می شود ، زیرا در اینجا مقاله نحوه محاسبه ناحیه رومبوس ، با دانستن اندازه مورب بزرگتر و پایین ، جانبی و قطر دایره کتیبه شده توصیف می شود. در رومبوس.

محتوا

می توانید منطقه رومبوس را با فرمول های مختلف پیدا کنید. کافی است که از خواص این شکل و خصوصیات ارقام دیگر مطلع شوید ، زیرا می توان آن را به مثلث تقسیم کرد ، می توان آن را با یک موازی و غیره برابر کرد. در زیر چنین فرمول هایی را مشاهده خواهید کرد. شما همچنین باید بدانید که چگونه رومبوس و یک موازی متفاوت هستند. با توجه به تعریف ریاضی. Rhombus شکل از چنین موازی با طرفین مساوی است ، اما برخلاف مربع - Rhombus هیچ زاویه ای مستقیم ندارد. اما مجموع دو زاویه در پایه رومبوس 180 درجه خواهد بود. تمام این دانش برای محاسبه ناحیه رومبوس ، سپس با جزئیات بیشتر ، مفید خواهد بود.

نحوه محاسبه ناحیه رومب - خصوصیات شکل

قبل از محاسبه ناحیه رومبوس ، بهتر است خود را با خواص این شکل آشنا کنید. در واقع ، به لطف دانش این خصوصیات ، اثبات احتمال یک فرمول خاص آسان تر خواهد بود. پیش از این قبلاً ذکر شده بود که رومبوس چیست. این رقم با همه طرف برابر با گوشه های تیز و گنگ مخالف است ، اما مستقیم نیست.

Rhombus دارای خواص زیر است:

همه طرف ها با یکدیگر برابر هستند
گوشه هایی که در مقابل یکدیگر قرار دارند نیز برابر هستند
مورب این رقم بیسکتور است ، در نقطه تقاطع به بخش های مساوی تقسیم می شوند
موربها همچنین در مرکز رومبوس و در زاویه های راست تقاطع می کنند
طرفهای مخالف ارقام نمی توانند تقاطع کنند ، حتی اگر اشعه را گسترش دهید ، آنها مانند یک موازی موازی هستند.

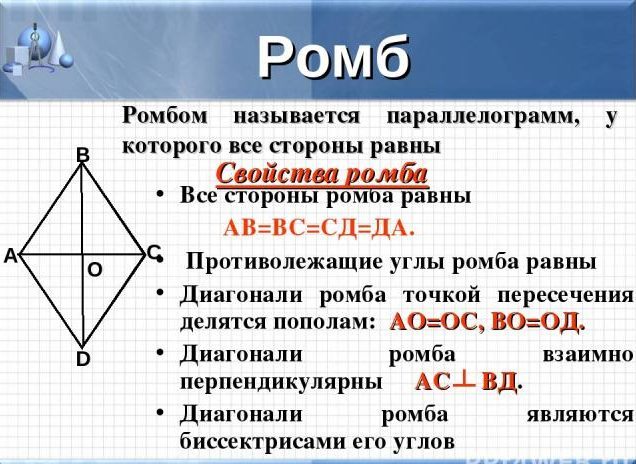
مهم: لطفاً توجه داشته باشید که رومبوس را می توان به چهار مثلث مستطیل شکل تقسیم کرد ، که در منطقه برابر خواهد بود ، یا با دو مثلث یکسان یکسان ، به تصویر بالا مراجعه کنید.

چگونه می توان مساحت رومبوس را محاسبه کرد؟

بنابراین ، بیایید دریابیم که چگونه منطقه رومبوس محاسبه می شود. بیایید از فرمول منطقه مستطیل استفاده کنیم ، جایی که:

s \u003d a • bجایی که a ، b طرف های مستطیل هستند.

به طوری که نحوه حذف فرمول منطقه رومبوس از این فرمول مشخص است ، ببینید توضیح:

یک رومبوس بکشید ، ارتفاع را به پایه Rhombus BH بسازید.
از نقطه D تا خط تبلیغ ، همچنین ارتفاع CH1 را بکشید.
معلوم است که مثلث ABH و مثلث CH1D از دو طرف مشترک با یکدیگر برابر هستند ، در پوشش بین آنها.
بنابراین آه \u003d dh1. مساحت مربع حاصل برابر با مساحت رومبوس خواهد بود
بنابراین BH • HH1 - این منطقه از رومبوس است ، به عبارت دیگر ، کار BH Rhombus به سمت AD و منطقه R Rhombus خواهد بود ، زیرا HH1 \u003d BC ، و BH است ارتفاع

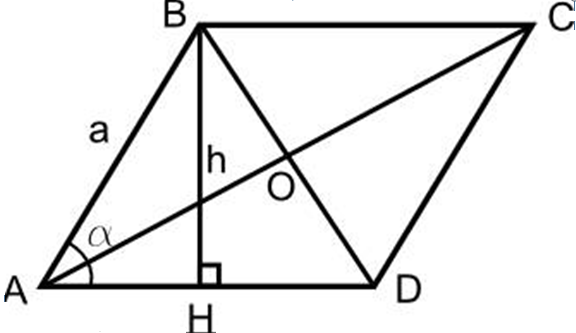
این از اثبات این است که:

s rhombus \u003d a • h و در واحدهای مربع اندازه گیری می شود.

چگونه می توان منطقه Rhombus را با دانستن گوشه و سمت شکل هندسی پیدا کرد؟

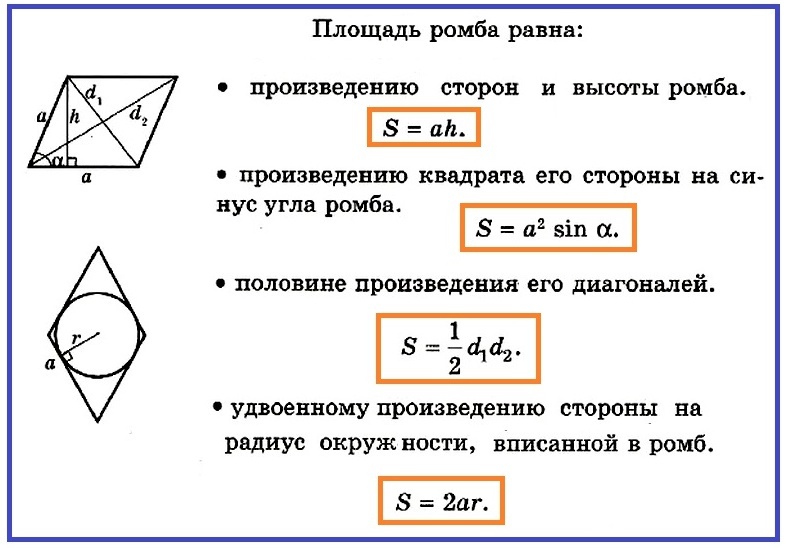
اکنون می دانیم که فرمول منطقه رومبوس چگونه به نظر می رسد ، می توانیم یک منطقه Rhomba را در همان فرمول پیدا کنیم ، می دانیم که طرف رومبوس با طرف رومب برابر است ، به عنوان مثال ، در پایه تیز است ، مانند عکس زیر

S \u003d A • H

اما در مورد ما ، ما به ارتفاع رومبوس ناشناخته هستیم ، باید آن را پیدا کرد. برای انجام این کار ، شما باید یک مثلث مستطیل شکل را در نظر بگیرید ، که معلوم شد وقتی ارتفاع به پایه رومبوس کشیده شد.

در این مثلث شناخته شده است hypotenuse و ∠α. برای محاسبه مساحت کل شکل ، باید ارتفاع پیدا کنید. ولی h \u003d a • گناه آنها. بنابراین منطقه یک موازی موازی برابر (Rhombus) است:

s \u003d a • a • گناه آنها تبر \u003d a² • Sinown.

فرمول های محاسبه مساحت رومبوس — منطقه شکل

چگونه می توان مساحت رومبوس را با دانستن مورب های آن محاسبه کرد؟

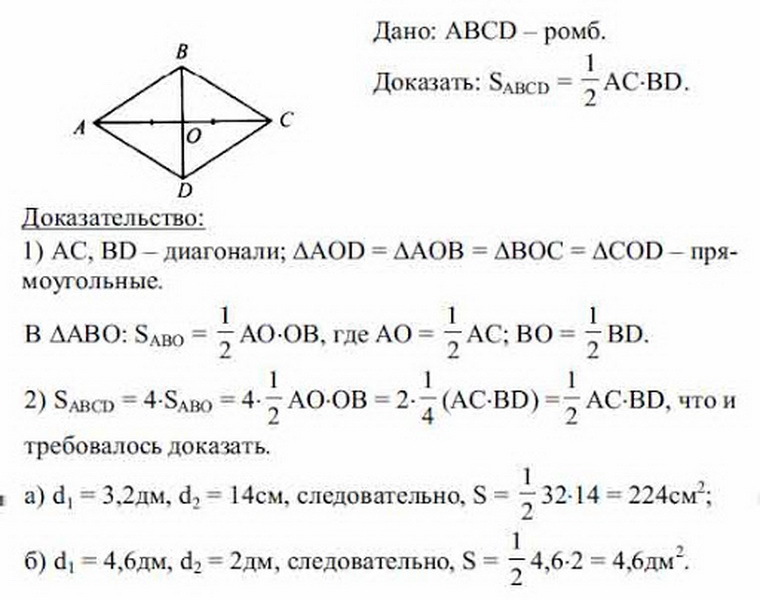
برای پیدا کردن فرمول ناحیه رومبوس ، هنگامی که فقط (A ، B) مورب ها شناخته شده اند ، مثال زیر باید در نظر گرفته شود. BCDA داده می شود - Rhombus و می دانید که مورب ها با چه برابر هستند. اکنون لازم است منطقه S از یک موازی موازی از نظر مورب ها پیدا شود.

پیش از این ، خواص رومب قبلاً در نظر گرفته شده بود. مورب های رومبوس برابر هستند ، در نقطه تقاطع آنها به بخش های مساوی تقسیم می شوند. از این نتیجه می گیرد که تمام مثلث هایی که در شکل در نتیجه از تقاطع هر دو مورب حک شده اند نیز با یکدیگر برابر هستند و مستطیل شکل هستند (از سه طرف). برای پیدا کردن ناحیه رومبوس ، کافی است که مساحت یک مثلث را پیدا کنید و داده های به دست آمده توسط 4 را ضرب کنید.

در کل ، معلوم است که:

S Rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC ، Total Square S Romm \u003d کار A • B (مورب) توسط دو مورد تقسیم می شود: s \u003d 1/2 a • b

چگونه می توان مساحت رومبوس را محاسبه کرد ، با دانستن سمت آن و شعاع دایره ای که در آن نوشته شده است؟

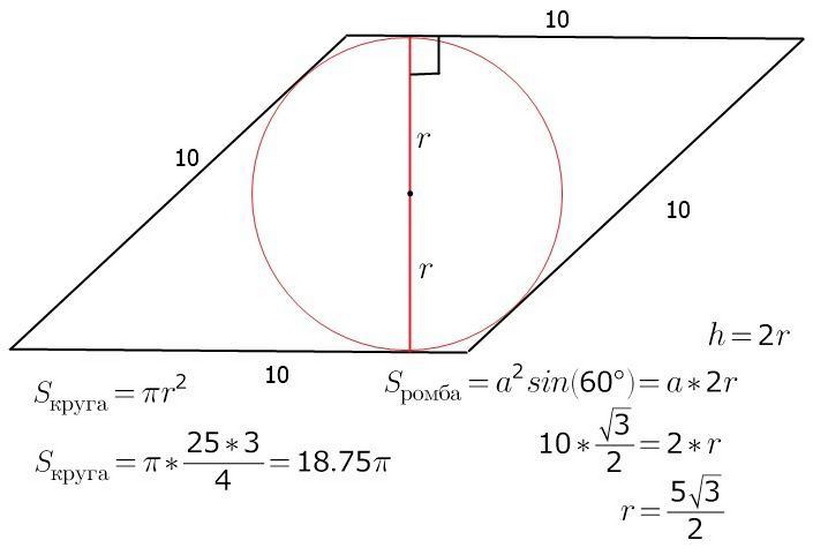
مساحت رومبوس را می توان با دانستن r - شعاع و a - طول طرف شکل محاسبه کرد. در حال حاضر مشخص شده است که S - منطقه شکل برابر با کار B - سمت در H - ارتفاع خواهد بود. از طریق مرکز دایره ، مرکز تقاطع A نیز خواهد بود ، B مورب های رومبوس است. ارتفاع و در همان زمان قطر رومبوس را انجام دهید. تصویر نشان می دهد که ارتفاع شکل دو شعاع دایره است. اکنون پیدا کردن منطقه خود Rhombus آسان خواهد بود: