Wie berechnet man die Fläche des Rhombus?

In diesem Artikel erfahren Sie, wie Sie den Bereich des Rhombus mit verschiedenen Methoden finden. Dank dieser Formeln kann es leicht durch Geometrieprobleme gelöst werden, da der Artikel hier beschreibt, wie die Fläche des Rhombus berechnet werden kann, wobei die Größe der Diagonale des größeren und niedrigeren, Seiten- und Durchmessers des eingeschriebenen Kreises kennt im Rhombus.

Inhalt

Sie können den Bereich des Rhombus durch verschiedene Formeln herausfinden. Es reicht aus, die Eigenschaften dieser Figur und Eigenschaften anderer Figuren zu kennen, da der Rhombus in Dreiecke unterteilt werden kann, es kann mit einem Parallelogramm usw. gleichgesetzt werden. Im Folgenden sehen Sie solche Formeln. Sie müssen auch wissen, wie sich Rhombus und ein Parallelogramm unterscheiden. Nach der mathematischen Definition. Der Rhombus ist eine Figur eines solchen Parallelogramms mit gleichen Seiten, aber im Gegensatz zum Quadrat hat der Rhombus keine geraden Winkel. Aber die Summe der beiden Winkel an der Basis des Rhombus beträgt 180 Grad. All dieses Wissen wird nützlich für die Berechnung des Bereichs des Rhombus und dann ausführlicher.

Wie man die Fläche des Rhombus berechnet - die Eigenschaften der Figur

Vor der Berechnung des Bereichs des Rhombus ist es besser, sich mit den Eigenschaften dieser Figur vertraut zu machen. Dank der Kenntnis dieser Merkmale wird es in der Tat einfacher sein, die Wahrscheinlichkeit einer bestimmten Formel zu beweisen. Früher wurde bereits erwähnt, was Rhombus ist. Es ist eine Figur mit gleicher Seiten, die entgegen den entgegengesetzten scharfen und dummen Ecken entspricht, aber nicht gerade.

Der Rhombus hat die folgenden Eigenschaften:

alle Seiten sind gleich zueinander
die gegenüberliegenden Ecken sind ebenfalls gleich
die Diagonalen dieser Figur sind Bisektoren, die am Schnittpunkt in gleiche Segmente unterteilt sind
die Diagonalen kreuzen sich auch in der Mitte des Rhombus und im rechten Winkel
die gegenüberliegenden Seiten der Figuren können sich nicht schneiden, selbst wenn Sie die Strahlen ausdehnen, sind sie parallel, wie ein Parallelogramm.

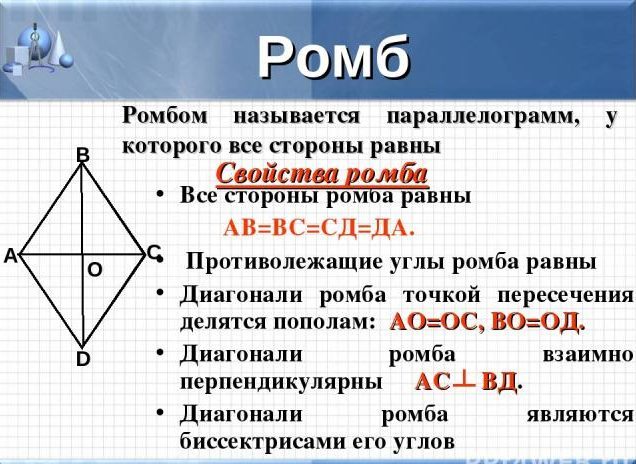
WICHTIG: Bitte beachten Sie, dass der Rhombus in vier rechteckige Dreiecke unterteilt werden kann, die im Bereich gleich oder durch zwei gleichseitige identische Dreiecke sind, siehe das Bild oben.

Wie berechnet man die Fläche des Rhombus?

Lassen Sie uns also herausfinden, wie der Rhombusbereich berechnet wird. Nutzen wir die Formel für den Bereich des Rechtecks, wo:

S \u003d a • bwo a, b die Seiten des Rechtecks \u200b\u200bsind.

So dass klar ist, wie man die Formel des Bereichs des Rhombus aus dieser Formel entzieht, siehe erläuterung:

Zeichnen Sie einen Rhombus, machen Sie eine Höhe zur Basis des BH -Rhombus.
Zeichnen Sie auch von Punkt D zur Anzeigenlinie auch eine CH1 -Höhe.
Es stellt sich heraus, dass das Dreieck ABH und das Dreieck CH1D auf zwei gemeinsamen Seiten gleich zueinander sind, schren in der Abdeckung zwischen ihnen.
Also ah \u003d dh1. Die Fläche des resultierenden Quadrats entspricht der Fläche des Rhombus
Also BH • HH1 - Dies ist der Bereich des Rhombus, mit anderen Worten, die Arbeit des BH -Rhombus zur Seite von AD und ist der Bereich des Rhombus, da HH1 \u003d BC und BH der ist Höhe.

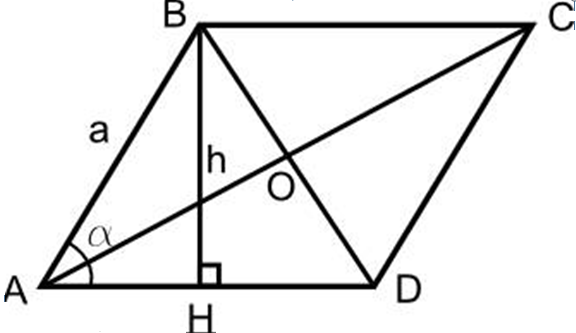
Aus dem Beweis folgt, dass:

S Rhombus \u003d a • h und in quadratischen Einheiten gemessen.

Wie finde ich den Bereich des Rhombus, der die Ecke und die Seite der geometrischen Figur kennt?

Jetzt wissen wir, wie die Formel des Rhombusbereichs aussieht. Wir können einen Rhomba -Bereich in derselben Formel finden, in dem die Seite des Rhombus gleich der Seite des Rhombus ist, zum Beispiel wie in der Basis, wie in Das Foto unten.

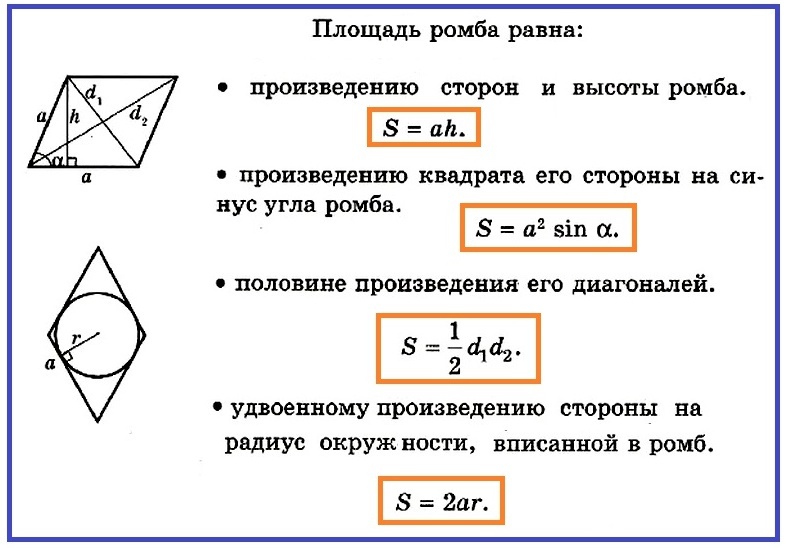
S \u003d a • h

Aber in unserem Fall sind wir der Höhe des Rhombus unbekannt, sollte es gefunden werden. Dazu müssen Sie ein rechteckiges Dreieck in Betracht ziehen, das sich herausstellte, als die Höhe zur Basis des Rhombus gezogen wurde.

In diesem Dreieck ist bekannt hypotenuse und test α. Um den Bereich der gesamten Abbildung zu berechnen, müssen Sie eine Höhe finden. ABER h \u003d a • Sünde sie. Die Fläche eines gleichseitigen Parallelogramms (Rhombus) lautet also:

S \u003d a • A • Sünde sie ax \u003d a² • Sinown.

Formeln zur Berechnung der Fläche des Rhombus — Der Bereich der Figur

Wie berechnet man die Fläche des Rhombus und kennt seine Diagonalen?

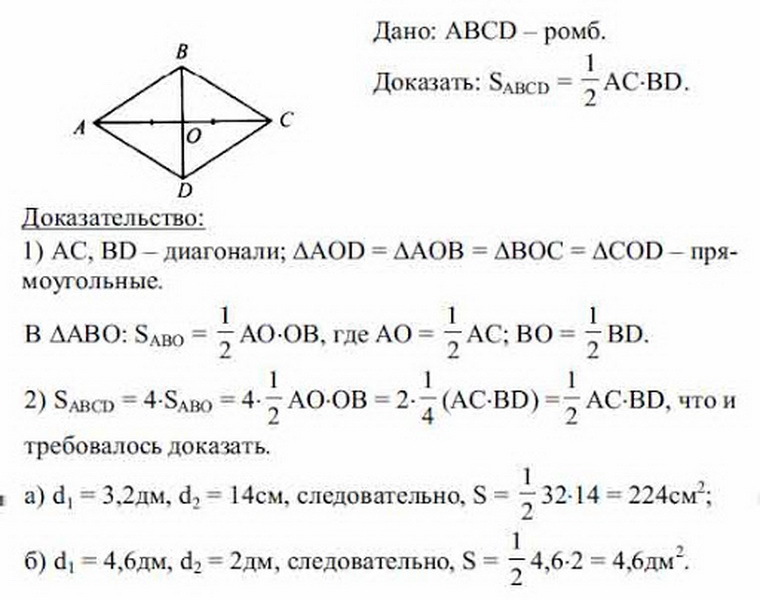
Um die Formel des Bereichs des Rhombus herauszufinden, wenn nur (a, b) Diagonale bekannt sind, sollte das folgende Beispiel in Betracht gezogen werden. BCDA wird gegeben - Rhombus und wissen, was die Diagonalen gleich sind. Jetzt ist es notwendig, S -Bereich eines gleichseitigen Parallelogramms in Bezug auf Diagonalen zu finden.

Zuvor wurden die Eigenschaften des Rhombus bereits berücksichtigt. Die Diagonalen des Rhombus sind gleich, am Schnittpunkt sind sie in gleiche Segmente unterteilt. Daraus folgt, dass alle Dreiecke, die in der Abbildung infolge des Schnittpunkts beider Diagonalen eingeschrieben sind, ebenfalls gleich sind und sie rechteckig sind (auf drei Seiten). Um den Bereich des Rhombus zu finden, reicht es aus, den Bereich eines Dreiecks zu finden und die mit 4 erhaltenen Daten zu multiplizieren.

Insgesamt stellt sich heraus, dass:

S Rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC,, Das Gesamtquadrat S romm wird \u003d Arbeit A • B (Diagonale) geteilt durch zwei: S \u003d 1/2 A • B

Wie berechnet man die Fläche des Rhombus und kennt seine Seite und den Radius des darin eingeschriebenen Kreises?

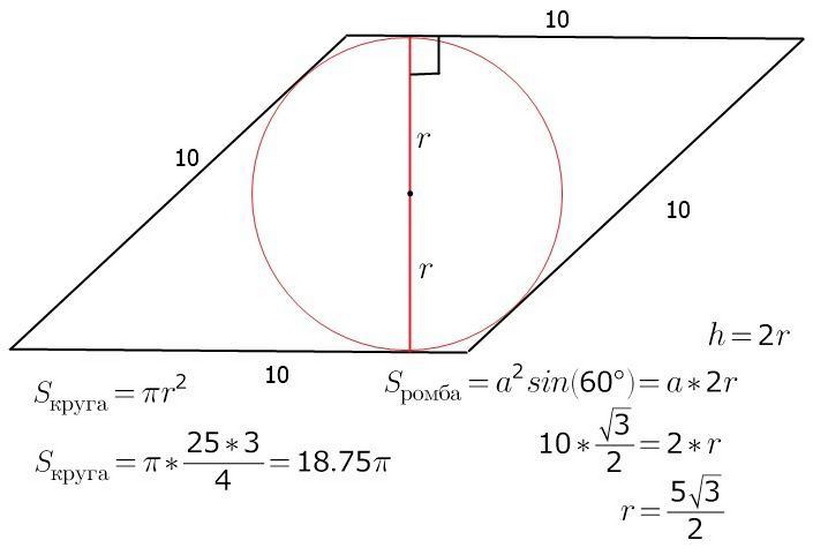
Die Fläche des Rhombus kann berechnet werden, indem R - Radius und a - die Länge der Seite der Abbildung kennt. Es ist bereits bekannt, dass S - der Bereich der Figur gleich der Arbeit b - der Seite auf H - Höhe entspricht. Durch die Mitte des Kreises wird es auch das Kreuzungszentrum A sein, B ist die Diagonale des Rhombus. Führen Sie die Höhe und gleichzeitig den Durchmesser des Rhombus aus. Das Bild zeigt, dass die Höhe der Figur zwei Radien des Kreises ist. Jetzt wird es leicht sein, den Bereich des Rhombus selbst zu finden: