Wie finde ich eine quadratische Fläche, wenn der Umkreis bekannt ist, diagonal? So finden Sie das Quadrat des Quadrats, das in den Kreis eingeschrieben und in der Nähe des Umfangs beschrieben wird: Formel, Beispiele für die Lösung von Problemen. Wie finde ich die Seite und Diagonale des Quadrats, wenn seine Fläche bekannt ist?

Lesen Sie den Artikel, um zu wissen, wie man die Quadratfläche auf unterschiedliche Weise findet.

Ein Quadrat ist ein gleichseitiges Rechteck. Dieses richtige und flache Viereck hat Gleichheit in allen Seiten, Ecken und Diagonalen. Aufgrund der Tatsache, dass es eine solche Gleichheit gibt, ist die Formel zur Berechnung der Fläche und anderer Eigenschaften im Vergleich zu anderen mathematischen Zahlen geringfügig verändert. Dies macht jedoch keine Aufgaben zu kompliziert. Lassen Sie uns alle Formeln und Lösungen für diesen Artikel analysieren.

Wie finde ich die Seite des Quadrats und kennt seine Fläche?

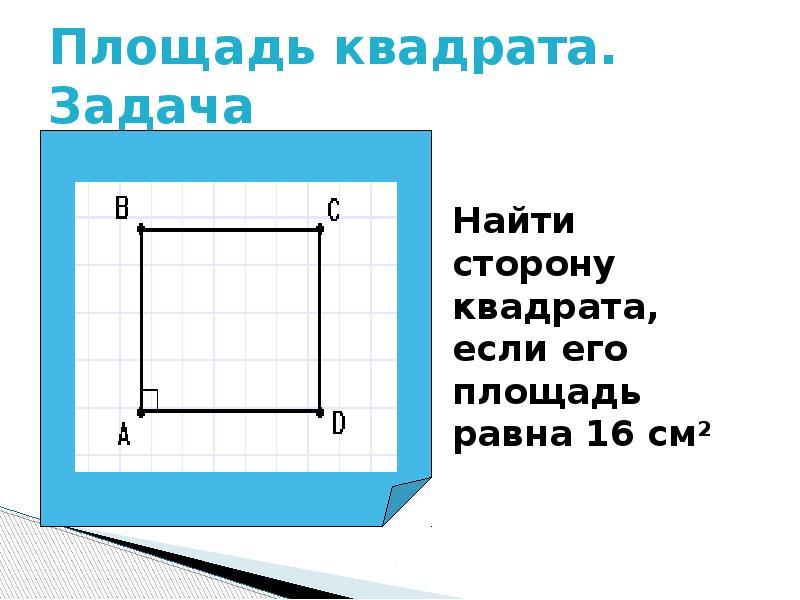
Quadrat S. Direkte und quadratische Quadrate werden nach der Formel berechnet: a Mal b.. Da der Platz jedoch eine vollständige Gleichheit der Parteien hat, wird seine Fläche gleich sein: S \u003d (a) im zweiten Grad.  Wie kann ich die Größe der Seite des Quadrats herausfinden und seine Fläche kennen?

• Wenn die Fläche des Quadrats bekannt ist, finden wir die Seite, indem wir die Fläche unter der Quadratwurzel berechnen.
• Zum Beispiel beträgt die Fläche des Quadrats 49, was ist dann die Seite gleich?
• 49 \u003d (a) im zweiten Grad. Lösung: a \u003d Wurzel von 49 \u003d 7. Antwort: 7.

Wenn Sie die Seite des quadratischen Quadrats finden müssen, deren Fläche zu lang ist, dann verwenden Sie den Taschenrechner. Wählen Sie zuerst die Anzahl des Bereichs und drücken Sie dann das Wurzelzeichen auf der Tastatur des Taschenrechners. Die resultierende Nummer wird die Antwort sein.

Wie finde ich eine quadratische Diagonale, wenn seine Fläche bekannt ist?

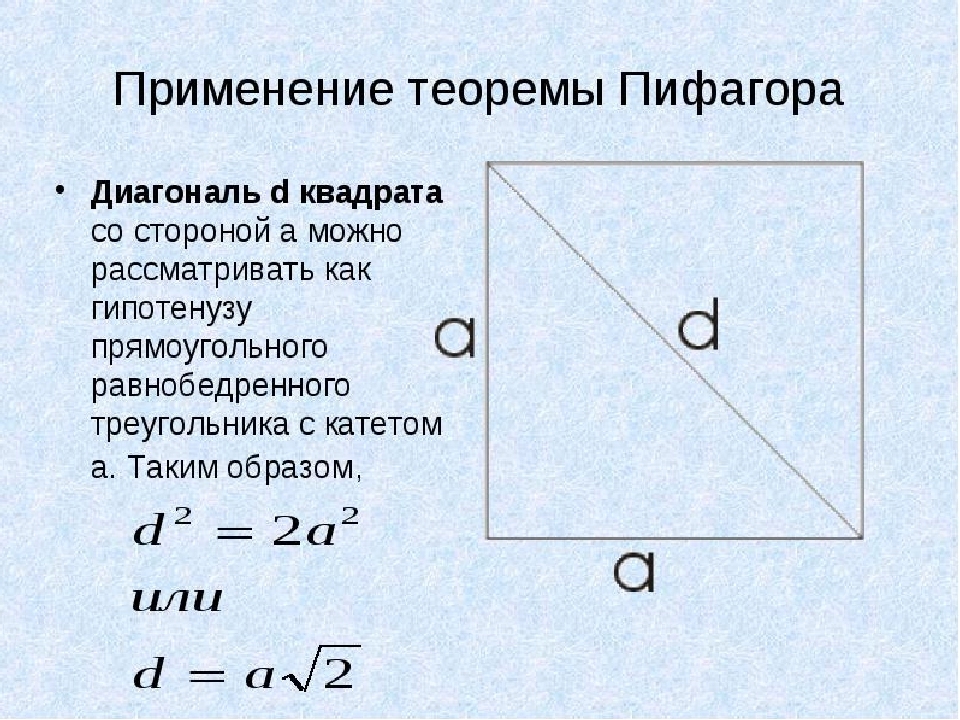
In diesem Beispiel werden wir den Pythagoras -Theorem verwenden. In einem Quadrat sind alle Seiten gleich und die Diagonale d. Wir werden als Hypotenuse eines rechteckigen iskellischen Dreiecks mit einem Bein betrachten a. Jetzt finden wir eine quadratische Diagonale, wenn seine Fläche bekannt ist:

• Um den gesamten pythagoräischen Satz nicht zu malen, entscheiden wir uns für die zweite Option: d \u003d Aising, wobei a die Seite des Quadrats ist.
• Wir kennen also die Fläche des Platz a \u003d √64 \u003d 8.
• Es stellt sich heraus D \u003d 8√2. Die Wurzel von 2 wirkt nicht die gesamte Nummer. In der Antwort können Sie so schreiben: d \u003d 8√2. Wenn Sie jedoch den Wert berechnen möchten, verwenden Sie den Taschenrechner: √2 \u003d 1,41421356237 und multiplizieren Sie mit 8, es stellt sich aus 11, 3137084.

Wichtig: In der Mathematik sind in der Regel keine Zahlen mit einer großen Anzahl von Zahlen als Antwort übrig. Es ist notwendig, mit der Wurzel zu runden oder zu verlassen. Die Antwort auf die Diagonale lautet daher, ob der Bereich 64 wie folgt beträgt: d \u003d 8√2.

Wie finde ich eine quadratische Fläche durch eine Diagonale?

Die Formel zum Finden der quadratischen Fläche durch die Diagonale ist einfach:

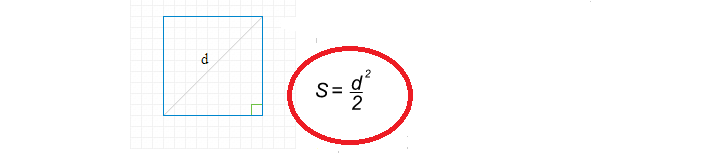
Schreiben wir nun eine Lösung, um die quadratische Fläche durch die Diagonale zu finden:

• Diagonal D \u003d 8.
• 8 auf dem Platz ist 64.
• 64 Teilen Sie durch 2 gleich 32.
• Die quadratische Fläche ist 32.

Rat: Diese Aufgabe hat eine andere Lösung durch den Pythagoras -Theorem, aber sie ist komplexer. Verwenden Sie daher die von uns untersuchte Lösung.

Wie finde ich eine quadratische Fläche, die seinen Umfang kennt?

Der Umfang des Quadratsquadrats P. - Dies ist die Summe aller Parteien. Um seine Fläche zu finden und seinen Umfang zu kennen, müssen Sie zunächst die Seite des Quadrats berechnen. Lösung:

• Angenommen, der Umkreis beträgt 24. Teilen Sie 24 in 4 Seiten, er stellt sich heraus, dass 6 - dies ist eine Seite.
• Jetzt verwenden wir die Formel, um die Fläche zu finden und zu wissen, was die Seite des Quadrats entspricht: S \u003d a in einem Quadrat, s \u003d 6 in einem Quadrat \u003d 36.
• Antworten: 36

Wie Sie sehen können, finden Sie einfach die Fläche.

Wie finde ich eine Fläche eines in einem Kreis mit einem bestimmten Radius eingeschriebenen Platz?

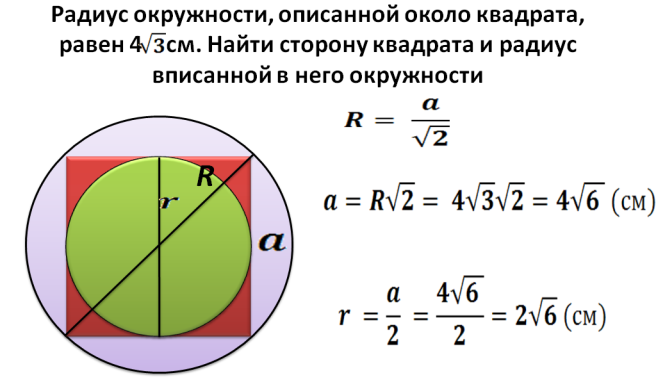
Radius R - Dies ist die Hälfte der Diagonale eines in einem Kreis eingeschriebenen Quadrats. Jetzt können wir eine Diagonale nach der Formel finden: d \u003d 2*r. Als nächstes finden wir das Quadrat des Quadrats in einem Kreis mit einem bestimmten Radius:

• Die Diagonale wird 2 mit dem Radius multiplizieren. Zum Beispiel ist der Radius 5, dann ist die Diagonale gleich 2*5=10.
• Es wurde oben beschrieben, wie man das Quadrat des Quadrats findet, wenn die Diagonale bekannt ist: S \u003d Diagonal in einem Quadrat, das in 2. s \u003d 10*10 geteilt ist und durch 2 \u003d 50 dividiert wird.
• Antworten - 50.

Diese Aufgabe ist etwas komplizierter, aber auch leicht zu lösen, wenn Sie alle Formeln kennen.

Wie finde ich eine Fläche eines Quadrats in der Nähe eines Kreises mit einem bestimmten Radius?

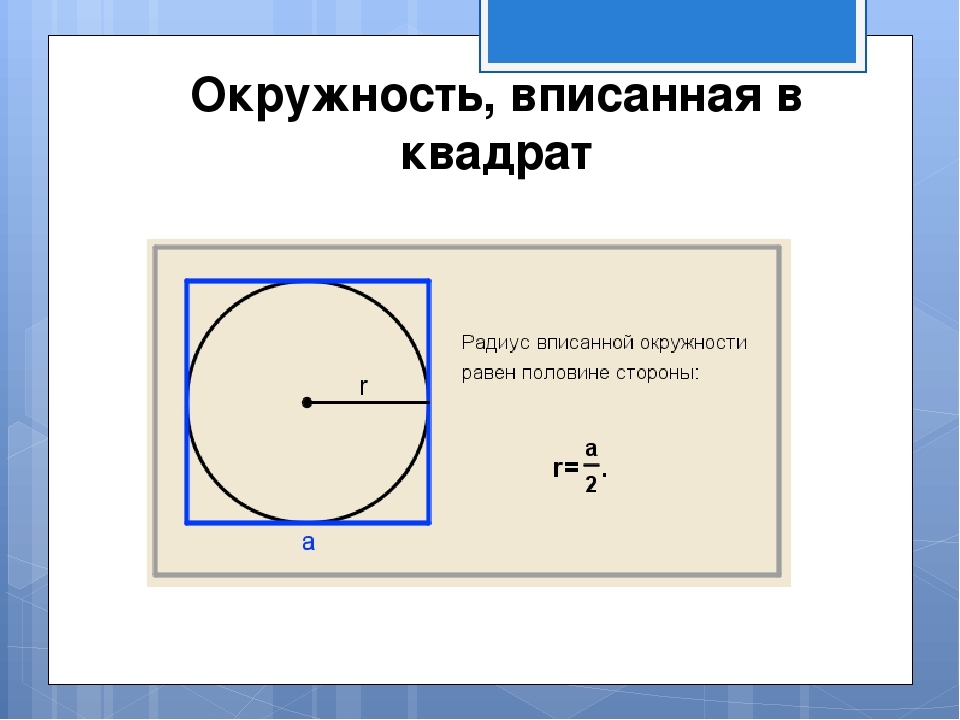
Das Bild zeigt, dass der Radius des eingeschriebenen Kreises der Hälfte der Seite entspricht. Die Seite befindet sich nach der umgekehrten Formel, die auf dem Bild dargestellt wird: a \u003d 2*r. Dann finden wir die Fläche des Quadrats in der Nähe des Kreises mit einem bestimmten Radius gemäß der Formel S \u003d und auf einem Quadrat. Lösung:

• Angenommen, der Radius beträgt 7. Die Seite des Quadrats A beträgt 2*7 \u003d 14.
• S \u003d 14 in einem Quadrat \u003d 196.

Wenn Sie die Essenz der Lösung solcher Probleme verstehen, können Sie sie schnell und einfach lösen. Schauen wir uns noch einige Beispiele an.

Beispiele für die Lösung von Problemen zum Thema "Square Square"

Um das abgedeckte Material zu reparieren und alle Formeln zu erinnern, müssen mehrere Beispiele für Probleme mit dem Thema „quadratischer Bereich“ gelöst werden. Wir beginnen mit einer einfachen Aufgabe und bewegen uns zur Lösung komplexer:

Jetzt wissen Sie, wie Sie die Formel für das Quadrat des Quadrats verwenden, was bedeutet, dass Sie jede Aufgabe erledigen können. Erfolg im zukünftigen Training!

Video: Berechnung der quadratischen Fläche