Come calcolare l'area del rombo?

In questo articolo imparerai come trovare l'area del rombo con vari metodi. Grazie a queste formule, sarà facilmente risolto dai problemi di geometria, perché qui l'articolo descriverà come calcolare l'area del rombo, conoscendo le dimensioni della diagonale del più grande e inferiore, laterale e diametro del cerchio inciso nel rombo.

Puoi scoprire l'area del rombo da diverse formule. È sufficiente conoscere le proprietà di questa figura e proprietà di altre figure, poiché il rombo può essere diviso in triangoli, può essere equiparato a un parallelogramma, ecc. Di seguito vedrai tali formule. Devi anche sapere come differiscono il rombo e un parallelogramma. Secondo la definizione matematica. Il rombo è una figura di un tale parallelogramma con lati uguali, ma a differenza del quadrato: il rombo non ha angoli diritti. Ma la somma dei due angoli alla base del rombo sarà di 180 gradi. Tutta questa conoscenza sarà utile per il calcolo dell'area del rombo, quindi in modo più dettagliato.

Come calcolare l'area del rombo - le proprietà della figura

Prima di calcolare l'area del rombo, è meglio familiarizzare con le proprietà di questa figura. In effetti, grazie alla conoscenza di queste caratteristiche, sarà più facile dimostrare la probabilità di una particolare formula. In precedenza era già menzionato cosa sia Rhombo. È una figura con uguale a tutti i lati uguali ad angoli acuti e stupidi opposti, ma non diritti.

Il rombo ha le seguenti proprietà:

• tutti i lati sono uguali tra loro
• anche gli angoli che giacciono uno di fronte all'altro sono uguali
• le diagonali di questa figura sono bisettori, nel punto di intersezione sono divisi in segmenti uguali
• le diagonali si intersecano anche al centro del rombo e ad angolo retto
• i lati opposti delle figure non possono intersecare, anche se estendi i raggi, sono paralleli, come un parallelogramma.

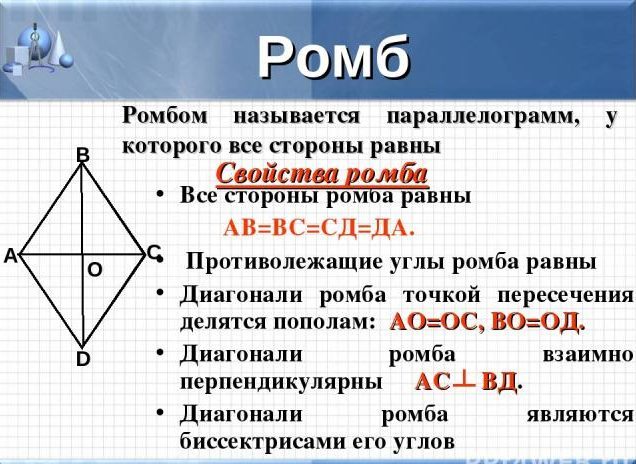
IMPORTANTE: Si prega di notare che il rombo può essere diviso in quattro triangoli rettangolari, che saranno uguali nell'area o da due triangoli identici equilaterali, vedere l'immagine sopra.

Come calcolare l'area del rombo?

Quindi, scopriamo come viene calcolata l'area del rombo. Approfittiamo della formula per l'area del rettangolo, dove:

• S \u003d a • bdove a, b sono i lati del rettangolo.

In modo che sia chiaro come rimuovere la formula dell'area del rombo da questa formula, vedi spiegazione:

1. Disegna un rombo, fai un'altezza alla base del rombo BH.
2. Dal punto D alla linea AD, disegna anche un'altezza CH1.
3. Si scopre che il triangolo ABH e il triangolo CH1D sono uguali tra loro su due lati comuni, ∠ nella copertura tra di loro.
4. Quindi ah \u003d dh1. L'area del quadrato risultante sarà uguale all'area del rombo
5. Quindi BH • HH1 - Questa è l'area del rombo, in altre parole, il lavoro del rombo BH sul lato dell'AD e sarà l'area S del rombo, poiché HH1 \u003d BC e BH è il altezza.

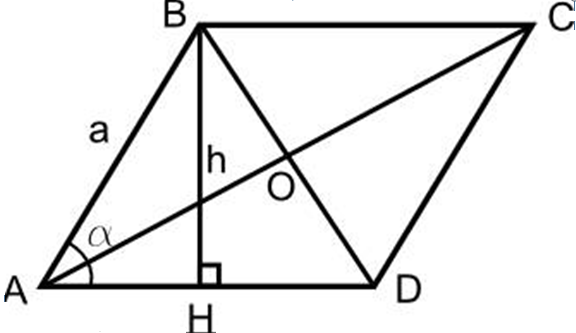
Segue dalla prova che:

• S rombus \u003d a • h e misurato in unità quadrate.

Come trovare l'area del rombo, conoscendo l'angolo e il lato della figura geometrica?

Ora sappiamo come appare la formula dell'area del rombo, possiamo trovare un'area rhomba sulla stessa formula, sapendo quale sia il lato del rombo uguale al lato del rombo, ad esempio acuto alla base La foto qui sotto.

• S \u003d a • h

Ma nel nostro caso, siamo sconosciuti all'altezza del rombo, dovrebbe essere trovato. Per fare ciò, dovrai considerare un triangolo rettangolare, che si è scoperto quando l'altezza è stata attratta dalla base del rombo.

In questo triangolo è noto ipotenusa e ∠α. Per calcolare l'area dell'intera figura, dovrai trovare un'altezza. MA h \u003d a • peccato loro. Quindi l'area di un parallelogramma equilatero (rombo) è:

• S \u003d A • A • sin che ax \u003d A² • sinown.

Come calcolare l'area del rombo, conoscendo le sue diagonali?

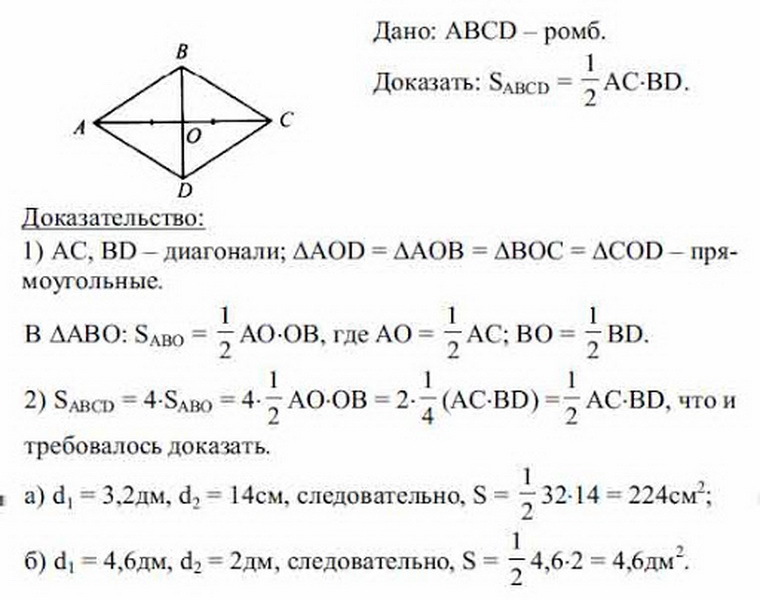
Per scoprire la formula dell'area del rombo, quando sono note solo (a, b) diagonali, si dovrebbe prendere in considerazione il seguente esempio. BCDA è dato - rombo e sapere quali sono le diagonali. Ora è necessario trovare l'area S di un parallelogramma equilatero in termini di diagonali.

In precedenza, le proprietà del rombo erano già state considerate. Le diagonali del rombo sono uguali, nel punto di intersezione sono divise in segmenti uguali. Da ciò ne consegue che tutti i triangoli che sono inscritti nella figura a seguito dell'intersezione di entrambe le diagonali sono uguali tra loro e sono rettangolari (su tre lati). Per trovare l'area del rombo, è sufficiente trovare l'area di un triangolo e moltiplicare i dati ottenuti per 4.

In totale, si scopre che:

• S rombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Totale quadrata s romm sarà \u003d lavoro a • b (diagonali) diviso per due: S \u003d 1/2 a • b

Come calcolare l'area del rombo, conoscendo il suo lato e il raggio del cerchio inscritto in esso?

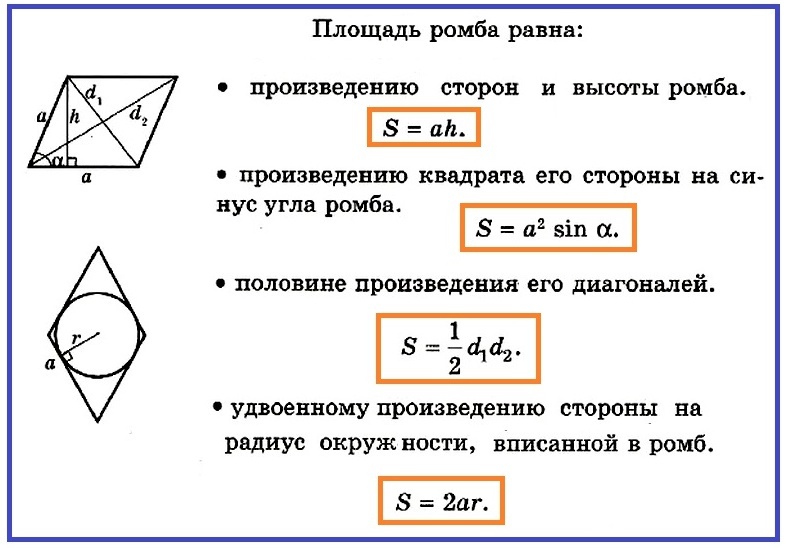
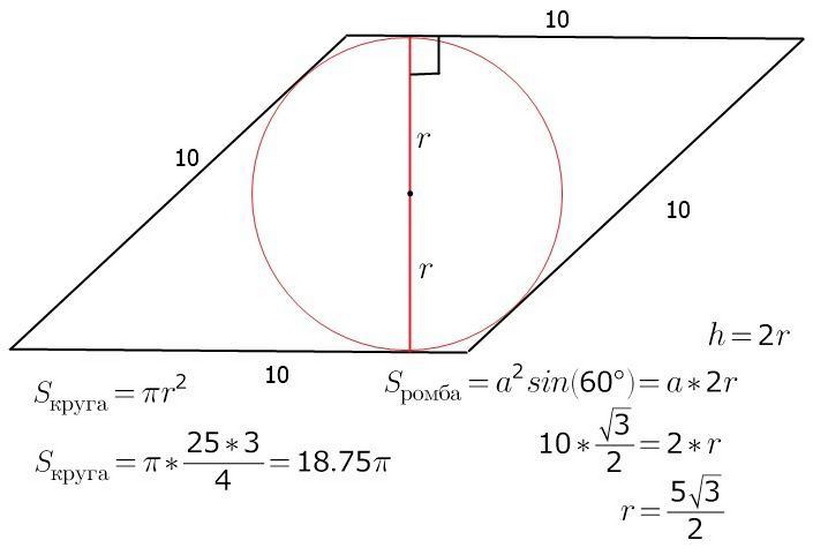
L'area del rombo può essere calcolata conoscendo il raggio r e A - la lunghezza del lato della figura. È già noto che s - l'area della figura sarà uguale al lavoro b - il lato su H - altezza. Attraverso il centro del cerchio, sarà anche il centro di intersezione A, B è le diagonali del rombo. Eseguire l'altezza e allo stesso tempo il diametro del rombo. L'immagine mostra che l'altezza della figura è due raggi del cerchio. Ora sarà facile trovare l'area del rombo stesso:

• S \u003d a • h \u003d a • 2r

Di seguito, vedere l'esempio dell'attività su questo argomento.

Vedi ancora tali articoli su questo argomento qui:

1. L'area del rettangolo, come trovare?
2. Come trovare un'area del cerchio?
3. Area quadrata - Formule.

Video: un esempio di come calcolare l'area del rombo