Formula volumena i površine pune površine kuglice, sfera kroz radijus i promjer kuglice: vrijednost. Primjeri izračunavanja površine i volumena kuglice, kroz radijus i promjer lopte: Opis. Kako pronaći volumen kuglice kroz površinu lopte: primjer

Članak će biti koristan školarcima i budućim podnositeljima zahtjeva koji se pripremaju za ispit.

Formula volumena kuglice kroz polumjer: Značenje

Volumen kuglice V izračunava se formulom (vidi dolje), gdje je R polumjer lopte, broj "pi" - π je matematička konstanta, ≈ 3.14.

Ova formula je baza!

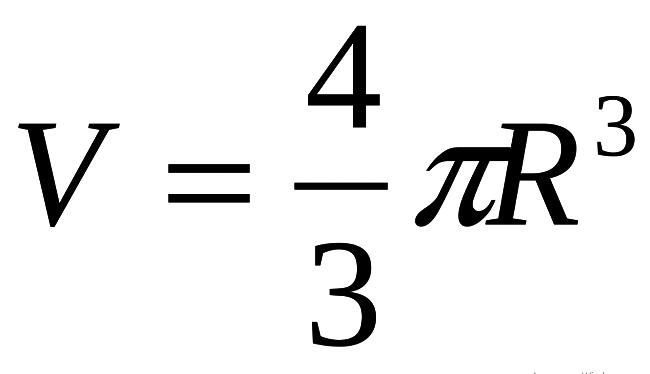
Formula volumena kuglice kroz promjer: Vrijednost

1. Koristite osnovnu formulu: v \u003d 4/3*π*r³.
2. Polumjer r je ½ promjera d ili r \u003d d/2.
3. Otuda: v \u003d 4/3*π*r³ → v \u003d (4π/3)*(d/2) ³ → v \u003d (4π/3)*(d³/8) → V \u003d πD.³/6.

Ili

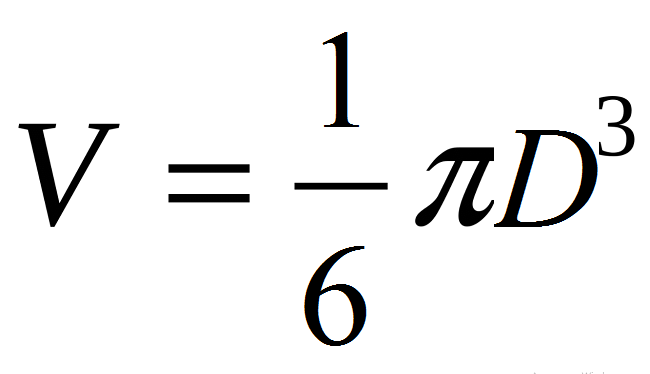
Primjeri izračunavanja volumena kuglice, kroz polumjer i promjer lopte: Opis

Zadatak 1.

Polumjer lopte je 10 cm. Pronađite njegov volumen.

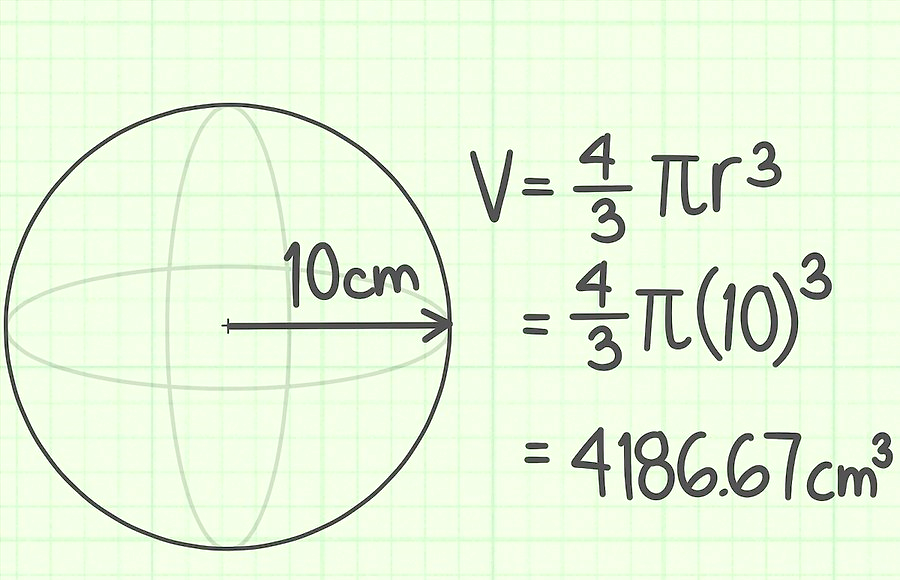
Zadatak 2.

Promjer kuglice je 10 cm. Pronađite njegov volumen.

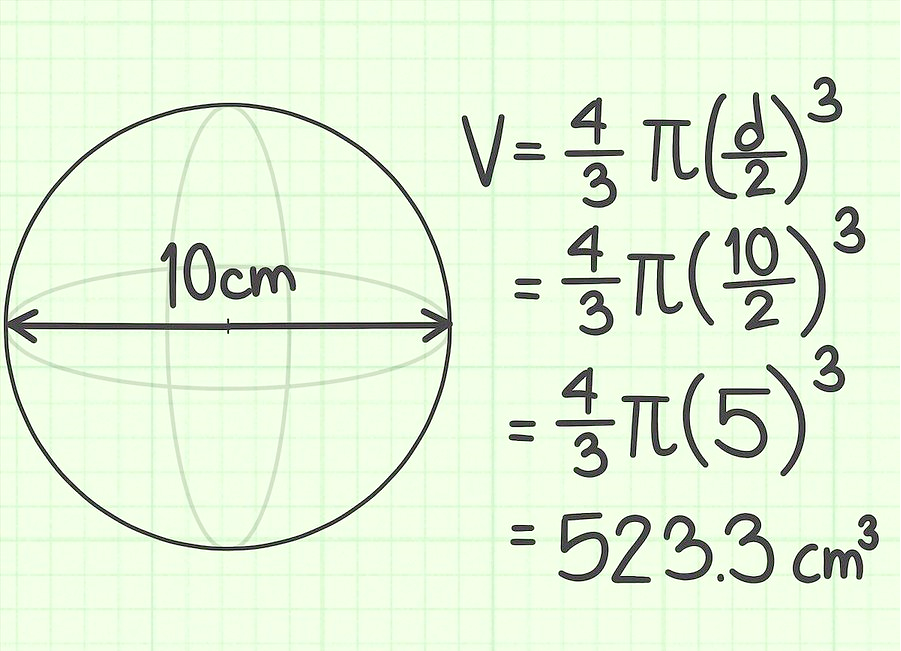
Zadatak 3.

Omjer promjera mjeseca i promjera zemlje 1: 4. Koliko je puta volumen zemlje veći od volumena Mjeseca?

Riješenje:

Odgovor: 64 puta.

Važno: Postoji mnogo internetskih kalkulatora koji vam omogućuju brzo pronalazak zadane vrijednosti. Na primjer, usluga Webmath.

Formula pune površine kuglice, sfera kroz polumjer: Značenje

Površina sfere/kuglice S izračunava se formulom (vidi dolje), gdje je R polumjer kuglice, broj "pi" - π je matematička konstanta, ≈ 3.14.

Ova formula je baza!

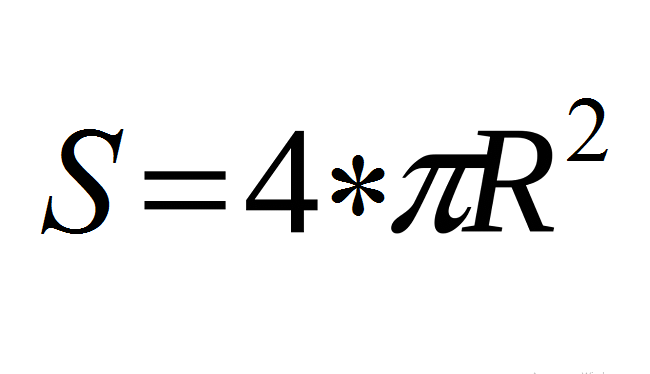
Formula pune površine kuglice, sfera kroz promjer: Vrijednost

1. Koristite osnovnu formulu: s \u003d 4*π*r².
2. Polumjer r je ½ promjera d ili r \u003d d/2.
3. Odavde: S \u003d 4*π*r² → S \u003d 4*π*(d/2) ² → S \u003d (4π)*(D²/4) → S \u003d (4πd²)/4 → S \u003d πD.².

Ili

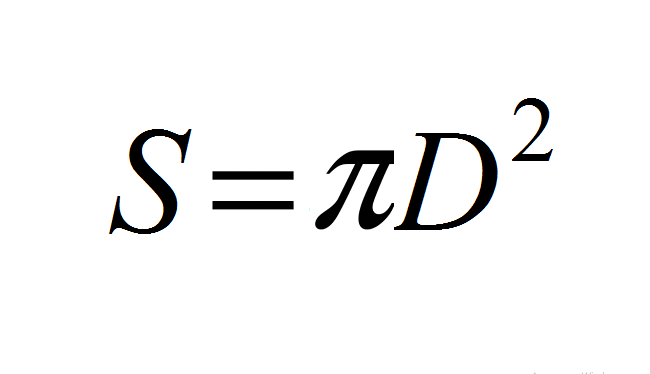
Primjeri izračunavanja površine, sfere kuglice, kroz polumjer i promjer lopte: Opis

Zadatak 4.

Zadatak 5..

Zadatak 6.

Kako pronaći volumen kuglice kroz površinu kuglice, sfera: Primjer rješavanja problema

Zadatak 7.

Zadatak 8.

Video: Koristite matematiku. Volumen i površina površine tijela rotacije.