Comment déterminer le milieu du segment à l'aide d'une circulaire?

Dans cet article, vous apprendrez à diviser ce segment ou ce segment avec l'aide d'un tel outil comme une boussole. Après tout, il n'y a pas toujours de règle à portée de main. Ces connaissances seront utiles dans la pratique.

Contenu

La géométrie est une matière étudiée à l'école et a une application dans la pratique. Grâce à la connaissance de cet élément, vous pouvez découvrir la zone, le volume d'une figure particulière ou un conteneur, ainsi que de diviser facilement le segment en deux à l'aide d'outils assistants. Nous apprendrons davantage sur la façon de déterminer le milieu du segment à l'aide d'un circul.

Comment déterminer le milieu du segment à l'aide d'une boussole?

Il est intéressant qu'il soit possible de déterminer le milieu du segment à l'aide d'une circulne sans souverain - cela a été prouvé par le maskeri italien au XVIIIe siècle. Le processus de construction est plus compliqué qu'avec ces deux outils, mais les connaissances à ce sujet n'interfèrent pas. Tout d'abord, nous déterminerons ce qu'est un segment. Le segment est appelé une ligne droite limitée de deux points. Et pour trouver le milieu du segment, vous devrez construire de nombreux cercles et trouver de nombreux points de leur intersection jusqu'à ce qu'il y ait le milieu du segment.

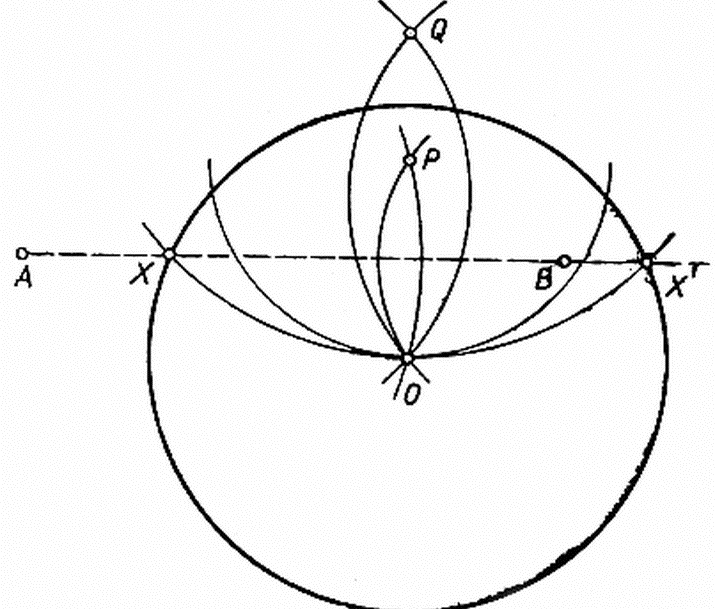
Si vous vous souvenez de la séquence, de la construction de cercles, le processus de détermination du milieu est simple. Tout d'abord, ils doublent le segment en construisant deux cercles avec un rayon égal à la longueur d'un segment donné, photo ci-dessous:

Cercles avec un rayon dans la longueur du segment

L'étape suivante consiste à construire un cercle avec le même rayon en haut à l'intersection de deux cercles, il ressemblera clairement à ceci:

De l'intersection du deuxième et du troisième cercle, dessinez un autre quatrième cercle du même rayon, ce dessin doit être obtenu:

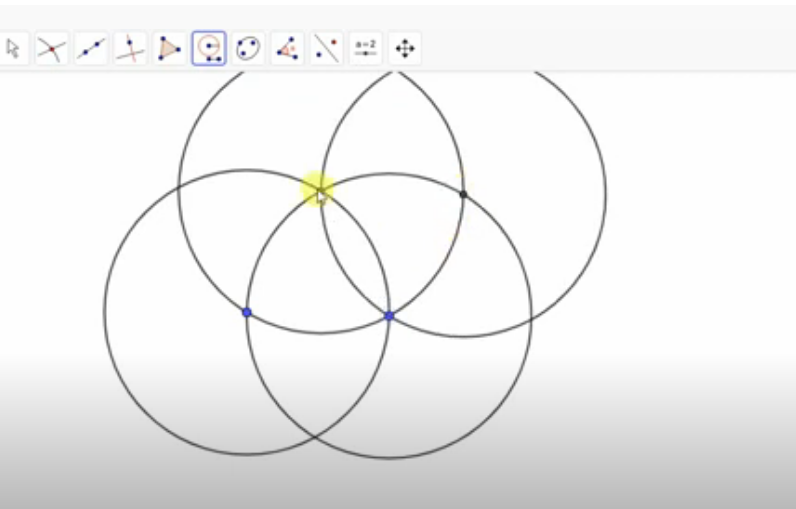
Ces cercles ont été construits pour obtenir un point (le troisième point, comme continuation du segment), il est à l'intersection du quatrième et deuxième cercle. Maintenant, laissez ce point et frottez deux cercles sur le dessus, ils n'en auront pas besoin.
Construisez un cercle avec un rayon deux fois plus que les précédents:

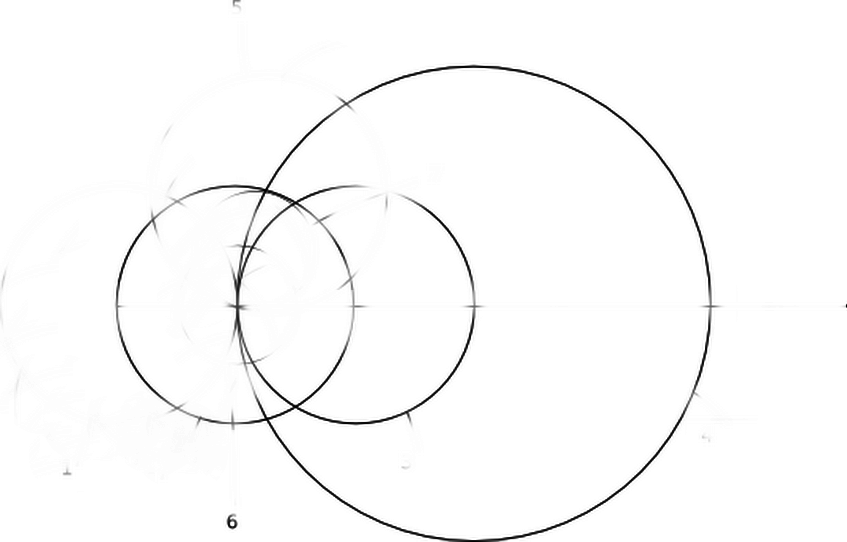
Marquez deux points d'intersection sur le premier cercle et grand. À travers ces deux points, dessinez des cercles avec le rayon du segment, et le point de leur intersection sera le milieu du segment.

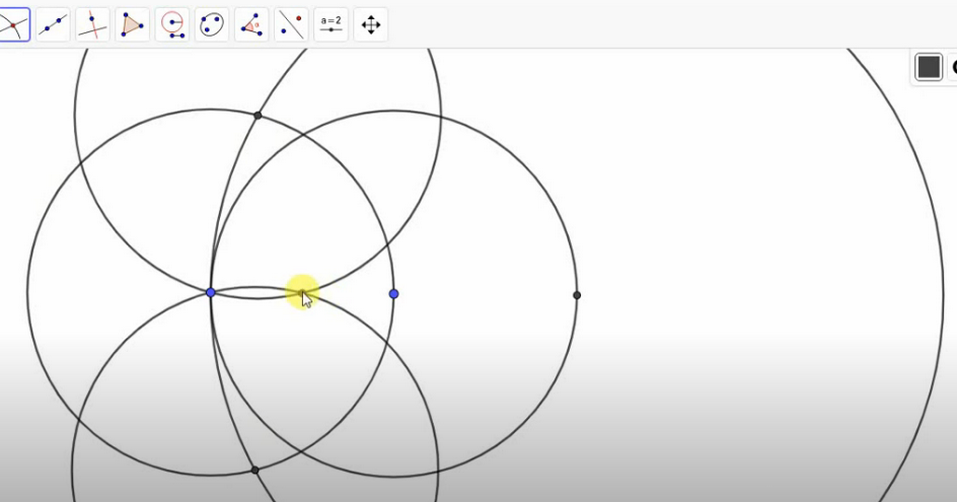
IMPORTANT: La recherche du milieu du segment se résume à quelques étapes. Initialement, le segment doit être allongé exactement deux fois en raison d'un cercle de plus grand diamètre, puis près des constructions et trouver le point même lui-même, qui le partage en deux.

Comment construire le milieu du segment avec un circul et une règle?

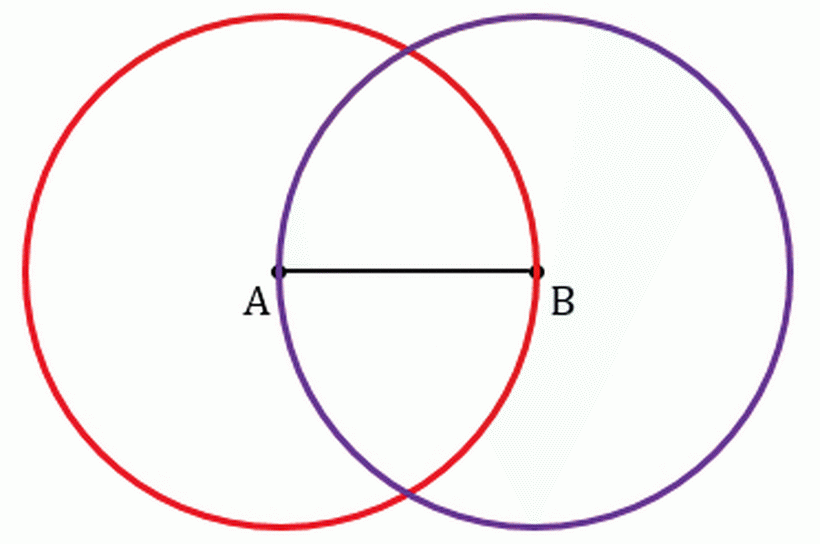
Vous pouvez également construire le milieu du segment à l'aide d'une règle circulaire. Le faire est beaucoup plus facile que dans la version précédente. Vous n'aurez pas besoin de dessiner de nombreux cercles de diamètres différents, et il suffit de construire seulement deux identiques, puis de dessiner une perpendiculaire à travers l'intersection avec les lignes de cercle. Cette perpendiculaire est également appelée milieu, ce qui signifie la ligne, qui est réalisée à un angle de 90 degrés par rapport au segment.

Ensuite, une classe de maître sur ce sujet sera présentée en détail et clairement:

Dessinez le segment souhaité sur la feuille de la cellule, il vous sera donc plus pratique pour vous de comprendre ce sujet.
Prenez la boussole et dessinez deux cercles avec un rayon de plus que le milieu du segment ou le rayon avec la longueur du segment - il n'y a pas de besoin particulier de dessiner des cercles trop grands, surtout si un segment d'une grande longueur.

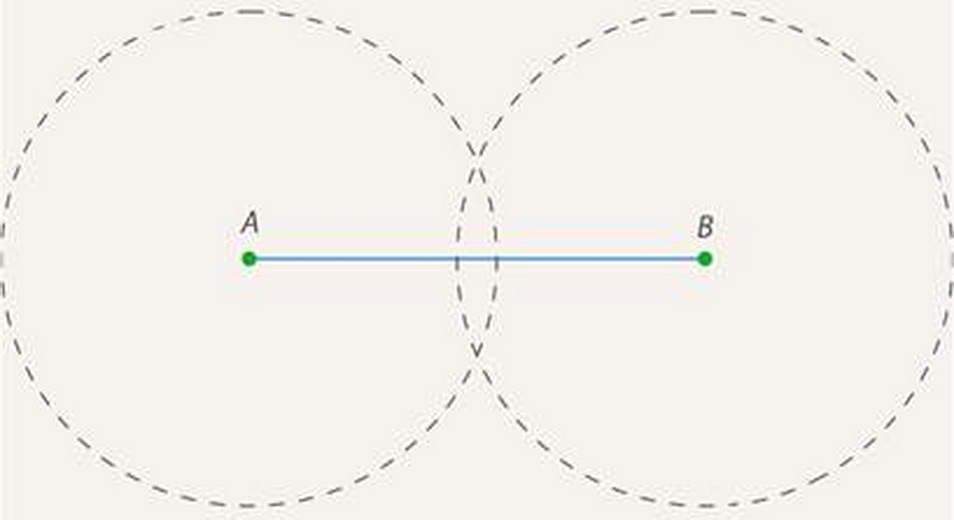
La figure ci-dessus montre que les cercles forment deux points d'intersection (au-dessus et en dessous). Vous aurez maintenant besoin d'une règle. Connectez ces deux points avec le milieu perpendiculaire. Le point de croisement de la ligne et du segment sera le milieu.

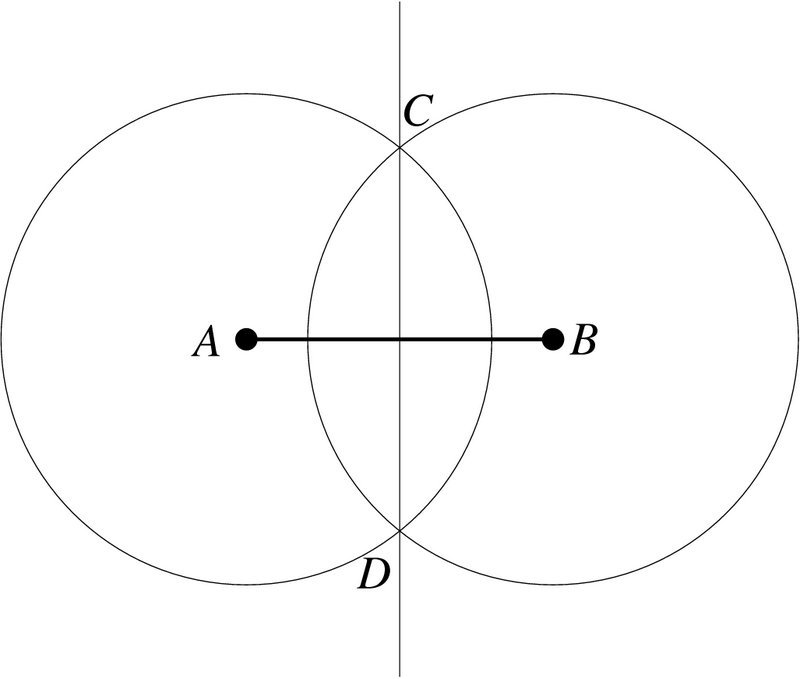
Ainsi, le point médian du segment a été trouvé, il ne fera plus de mal de prouver qu'il est CD - le milieu perpendiculaire, et il partage le segment de moitié. C'est facile de le faire. Après tout, deux cercles qui forment une ligne ont le même rayon, diamètre. Et en rond, tous les points sur la ligne sont également retirés de son centre. Les points C et D sont donc également situés aux mêmes distances des points A et B. La ligne qui relie les points D et C ne peut en être un dans l'avion. Et le point d'intersection sur le segment est à la même distance. Tout cela devait être clarifié.