Topun tam yüzeyinin hacmi ve alanı formülü, topun yarıçapı ve çapı boyunca küre: değer. Topun yarıçapı ve çapı boyunca yüzey alanının ve hacminin hesaplanması örnekleri: Açıklama. Topun hacmini topun yüzey alanından nasıl bulabilirim: Örnek

Makale, sınav için hazırlanan okul çocukları ve gelecekteki başvuru sahipleri için yararlı olacaktır.

Yarıçaptan topun hacminin formülü: anlam

V topunun hacmi formülle hesaplanır (aşağıya bakınız), burada R topun yarıçapıdır, “pi” - π matematiksel bir sabittir, ≈ 3.14.

Bu formül temeldir!

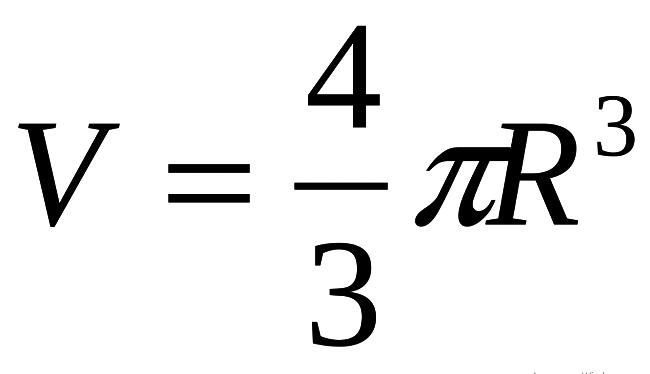
Topun Hacminin Formülü Çap içinden: Değer

1. Temel formülü kullanın: V \u003d 4/3*π*r³.
2. R yarıçapı ½ çapı D veya r \u003d d/2'dir.
3. Dolayısıyla: V \u003d 4/3*π*r³ → v \u003d (4π/3)*(d/2) ³ → v \u003d (4π/3)*(d³/8) → V \u003d πD.³/6.

Veya

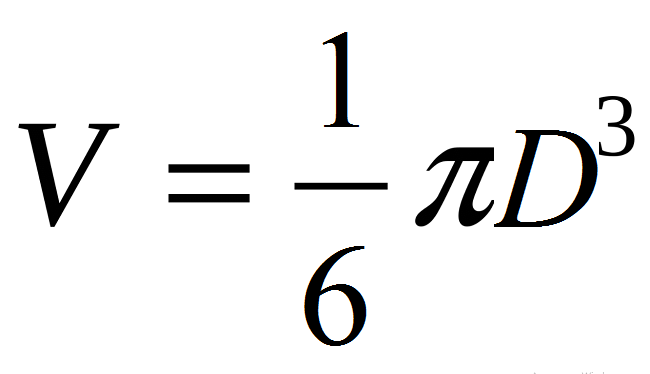
Topun hacmini hesaplama örnekleri, topun yarıçapı ve çapı üzerinden: Açıklama

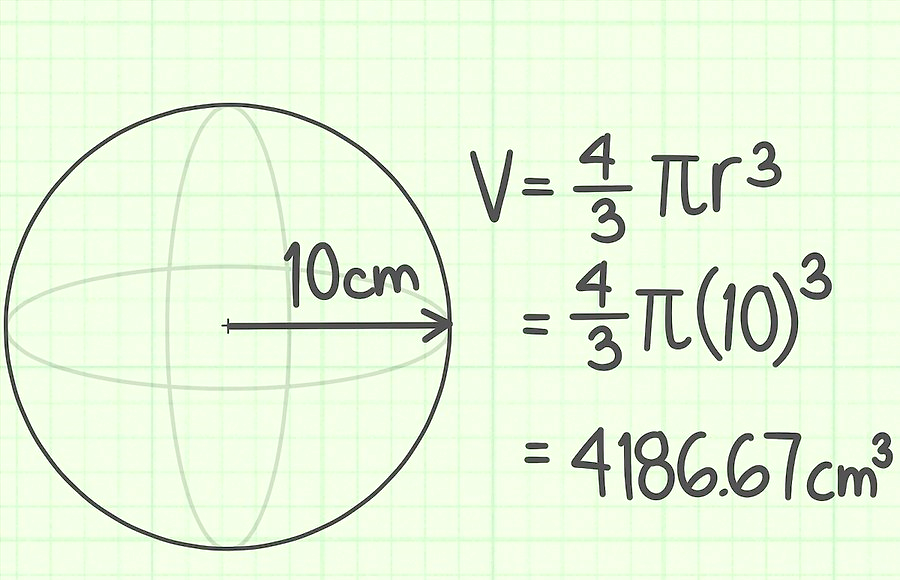
Görev 1.

Topun yarıçapı 10 cm'dir. Hacmini bulun.

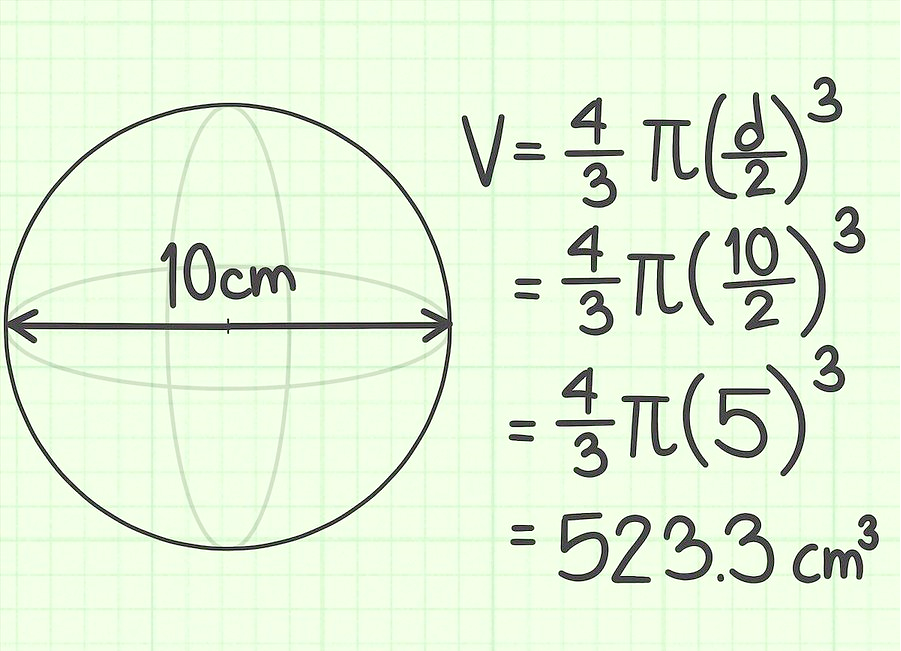
Görev 2.

Topun çapı 10 cm'dir. Hacmini bulun.

Görev 3.

Ayın çapı ve Dünya çapının oranı 1: 4. Dünyanın hacmi ayın hacminden kaç kez daha büyük?

Çözüm:

Cevap: 64 kez.

Önemli: Belirli bir değeri hızlı bir şekilde bulmanıza izin veren birçok çevrimiçi hesap makinesi vardır. Örneğin, hizmet Webmath.

Topun tam yüzeyinin formülü, yarıçaptan geçen küre: anlam

Kürenin/bilyanın yüzey alanı formülle hesaplanır (aşağıya bakınız), burada R topun yarıçapıdır, “Pi” - π Matematiksel bir sabittir, ≈ 3.14.

Bu formül temeldir!

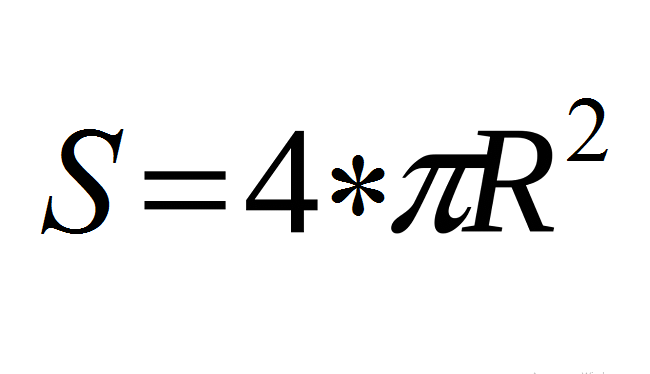
Topun tam yüzeyinin formülü, çaptan küre: değer

1. Temel formülü kullanın: S \u003d 4*π*r².
2. R yarıçapı ½ çapı D veya r \u003d d/2'dir.
3. Buradan: s \u003d 4*π*r² → s \u003d 4*π*(d/2) ² → s \u003d (4π)*(d²/4) → s \u003d (4πd²)/4 → S \u003d πD.².

Veya

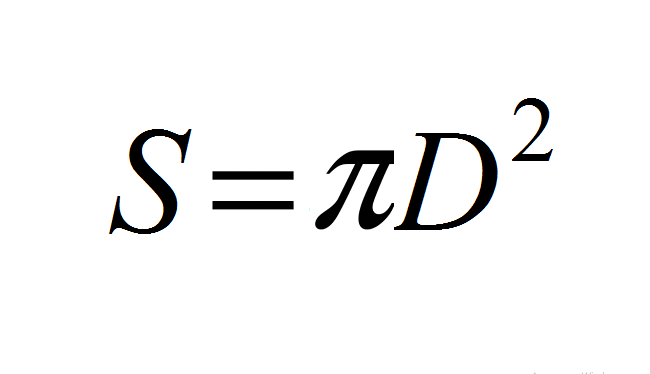
Topun yarıçapı ve çapı boyunca yüzey alanının, topun küresinin hesaplanmasına örnekler: açıklama

Görev 4.

Görev 5.

Görev 6.

Topun hacmini topun yüzey alanından nasıl bulabilirim, küre: Bir sorunu çözme örneği

Görev 7.

Görev 8.

Video: Matematik kullanın. Rotasyon gövdelerinin yüzeyinin hacmi ve alanı.