Σε αυτό το άρθρο, θα μάθετε πώς να διαιρέσετε αυτό ή αυτό το τμήμα με τη βοήθεια ενός τέτοιου εργαλείου ως πυξίδα. Μετά από όλα, δεν υπάρχει πάντα ένας χάρακα στο χέρι. Τέτοιες γνώσεις θα είναι χρήσιμες στην πράξη.
Περιεχόμενο
Η γεωμετρία είναι ένα θέμα που μελετάται στο σχολείο και έχει εφαρμογή στην πράξη. Χάρη στη γνώση αυτού του αντικειμένου, μπορείτε να μάθετε την περιοχή, τον όγκο ενός συγκεκριμένου αριθμού ή στο δοχείο, καθώς και να διαιρέσετε εύκολα το τμήμα στο μισό με τη βοήθεια βοηθών εργαλείων. Θα μάθουμε περαιτέρω πώς να καθορίσουμε τη μέση του τμήματος χρησιμοποιώντας ένα Circul.
Πώς να προσδιορίσετε τη μέση του τμήματος χρησιμοποιώντας μια πυξίδα;
Είναι ενδιαφέρον ότι είναι δυνατόν να προσδιοριστεί η μέση του τμήματος χρησιμοποιώντας ένα κυκλοφορία χωρίς χάρακα - αυτό αποδείχθηκε από το ιταλικό Maskeri τον δέκατο όγδοο αιώνα. Η διαδικασία κατασκευής είναι πιο περίπλοκη από ό, τι με αυτά τα δύο εργαλεία, αλλά η γνώση σχετικά με αυτό δεν θα παρεμβαίνει. Πρώτον, θα καθορίσουμε τι είναι ένα τμήμα. Το τμήμα ονομάζεται ευθεία γραμμή περιορισμένη κατά δύο σημεία. Και για να βρείτε τη μέση του τμήματος, θα πρέπει να χτίσετε πολλούς κύκλους και να βρείτε πολλά σημεία της διασταύρωσης τους μέχρι να υπάρξει η μέση του τμήματος.
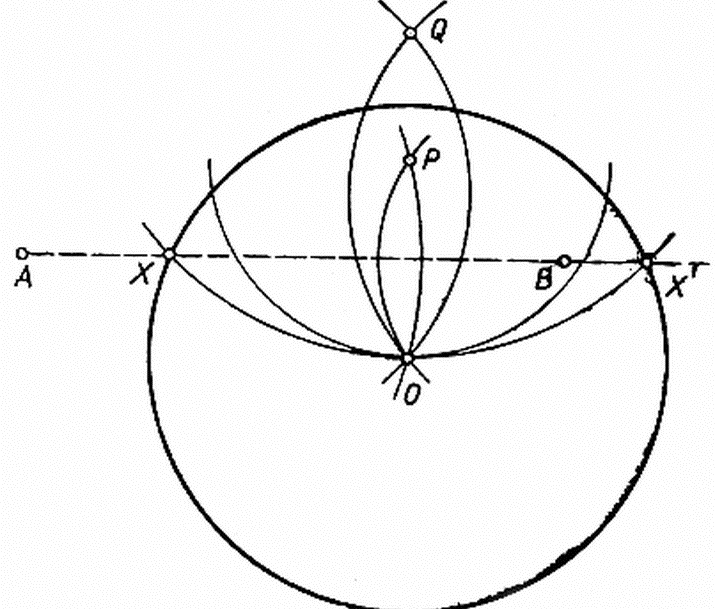
- Εάν θυμάστε την ακολουθία, η κατασκευή κύκλων, τότε η διαδικασία καθορισμού της μέσης είναι απλή. Πρώτον, διπλασιάζουν το τμήμα κατασκευάζοντας δύο κύκλους με ακτίνα ίση με το μήκος ενός δεδομένου τμήματος, φωτογραφία παρακάτω:
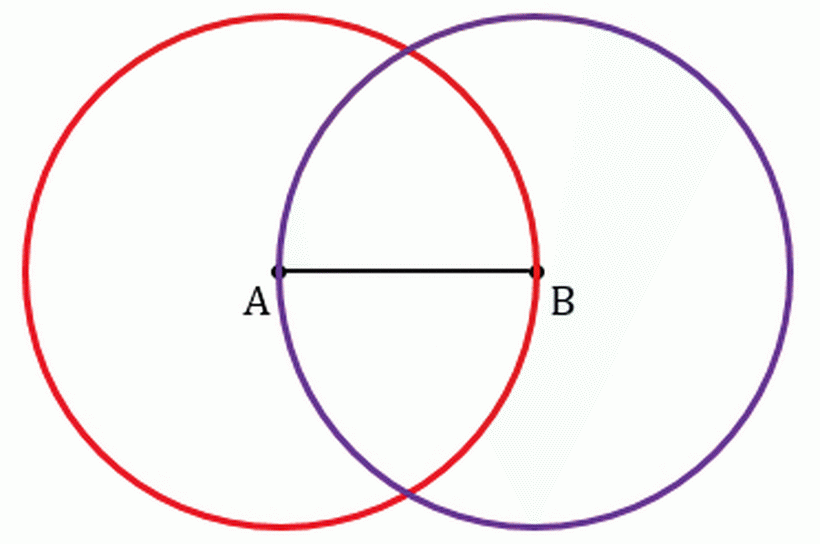
- Το επόμενο βήμα είναι να οικοδομήσουμε έναν κύκλο με την ίδια ακτίνα στην κορυφή στη διασταύρωση δύο κύκλων, θα μοιάζει σαφώς με αυτό:

- Από τη διασταύρωση του δεύτερου και του τρίτου κύκλου, σχεδιάστε έναν άλλο τέταρτο κύκλο της ίδιας ακτίνας, πρέπει να ληφθεί αυτό το σχέδιο:
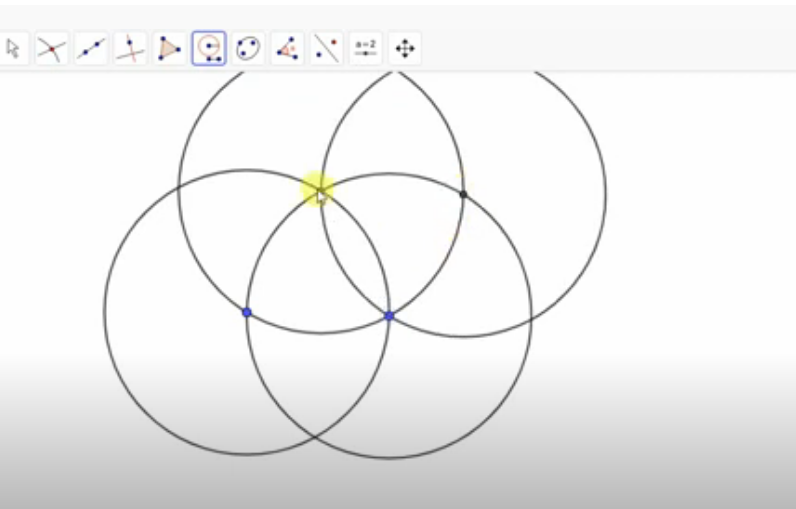
- Αυτοί οι κύκλοι χτίστηκαν για να πάρουν ένα σημείο (το τρίτο σημείο, ως συνέχεια του τμήματος), βρίσκεται στη διασταύρωση του τέταρτου και του δεύτερου κύκλου. Τώρα αφήστε αυτό το σημείο και τρίψτε δύο κύκλους στην κορυφή, δεν θα τα χρειαστούν.
- Δημιουργήστε έναν κύκλο με ακτίνα δύο φορές περισσότερο από τις προηγούμενες:
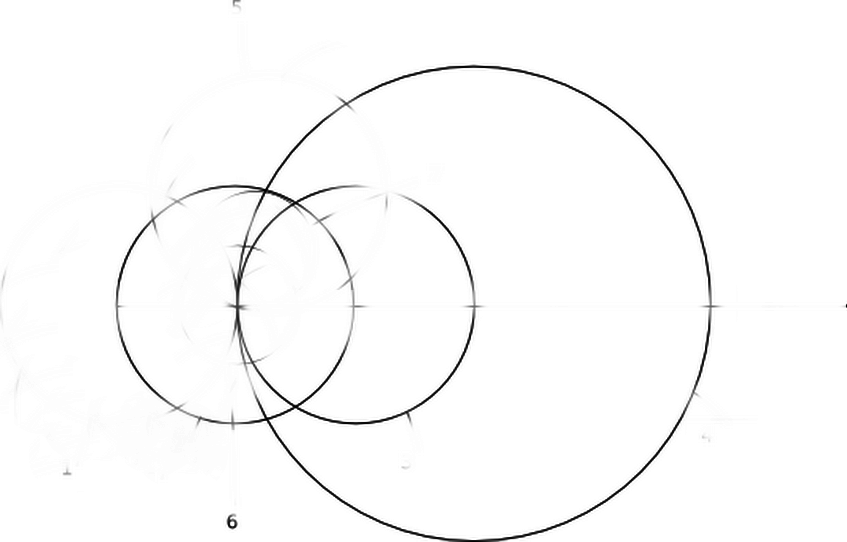
- Σημειώστε δύο σημεία διασταύρωσης στον πρώτο κύκλο και μεγάλο. Μέσα από αυτά τα δύο σημεία, τραβήξτε κύκλους με την ακτίνα του τμήματος και το σημείο της διασταύρωσης τους θα είναι το μέσο του τμήματος.
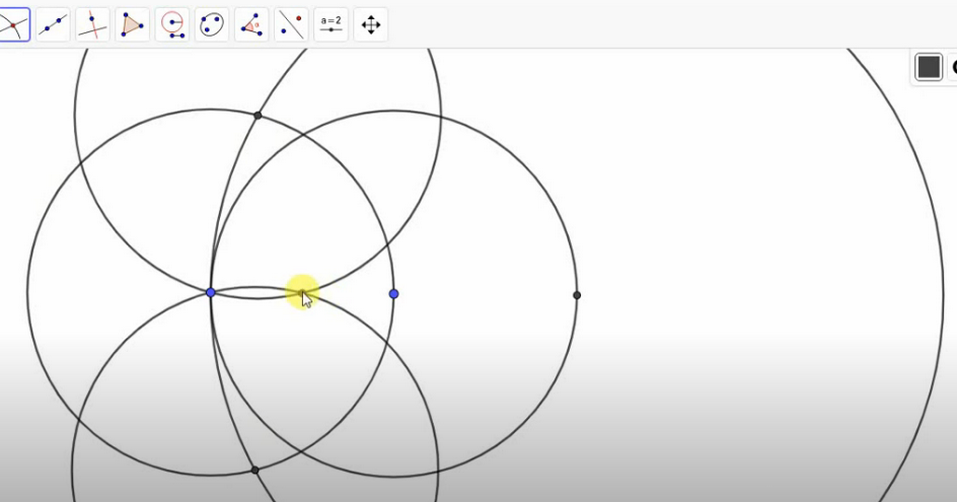
ΣΠΟΥΔΑΙΟΣ: Η αναζήτηση για τη μέση του τμήματος μειώνεται σε μερικά βήματα. Αρχικά, το τμήμα θα πρέπει να επιμηκυνθεί ακριβώς δύο φορές λόγω ενός κύκλου μεγαλύτερης διαμέτρου, και στη συνέχεια κοντά στις κατασκευές και να βρει το ίδιο το σημείο, ο οποίος το μοιράζεται στο μισό.
Πώς να οικοδομήσουμε τη μέση του τμήματος με ένα Circul και Chuner;
Μπορείτε επίσης να χτίσετε τη μέση του τμήματος χρησιμοποιώντας ένα Circul, Chuner. Για να γίνει αυτό είναι πολύ πιο εύκολο από ό, τι στην προηγούμενη έκδοση. Δεν θα χρειαστεί να σχεδιάσετε πολλούς κύκλους διαφορετικών διαμέτρων και αρκεί να χτίσετε μόνο δύο πανομοιότυπα και στη συνέχεια να σχεδιάσετε μια κάθετη μέσω της διασταύρωσης με τις γραμμές κύκλου. Αυτή η κάθετη ονομάζεται επίσης η μέση, που σημαίνει τη γραμμή, η οποία πραγματοποιείται υπό γωνία 90 βαθμών στο τμήμα.
Στη συνέχεια, μια κύρια τάξη σε αυτό το θέμα θα παρουσιαστεί λεπτομερώς και σαφώς:
- Σχεδιάστε το επιθυμητό τμήμα στο φύλλο στο κελί, οπότε θα είναι πιο βολικό να καταλάβετε αυτό το θέμα.
- Πάρτε την πυξίδα και τραβήξτε δύο κύκλους με ακτίνα περισσότερο από τη μέση του τμήματος ή την ακτίνα με το μήκος του τμήματος - δεν υπάρχει ιδιαίτερη ανάγκη να τραβήξετε πολύ μεγάλους κύκλους, ειδικά εάν ένα τμήμα μεγάλου μήκους.
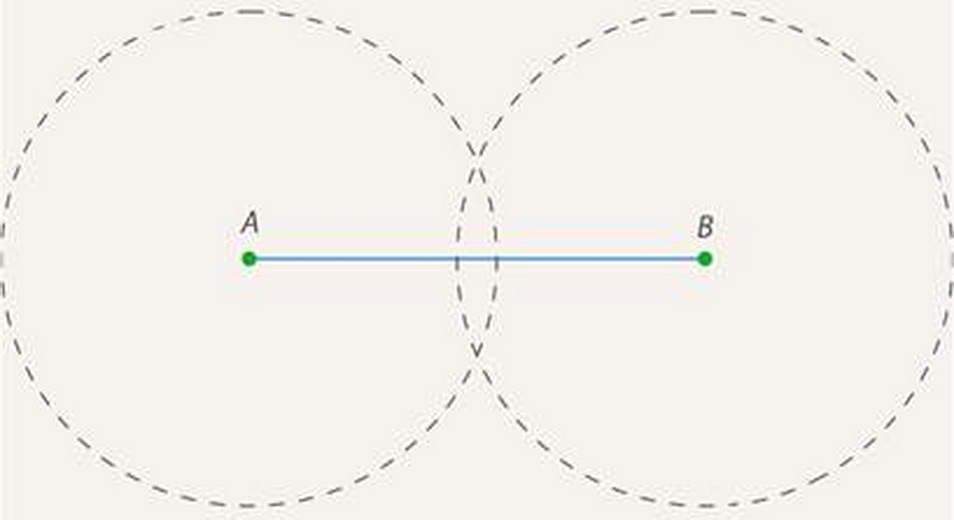
- Το παραπάνω σχήμα δείχνει ότι οι κύκλοι σχηματίζουν δύο σημεία διασταύρωσης (πάνω και κάτω). Τώρα θα χρειαστείτε έναν κυβερνήτη. Συνδέστε αυτά τα δύο σημεία με τη μεσαία κάθετη. Το σημείο διέλευσης της γραμμής και του τμήματος θα είναι το μέσο.
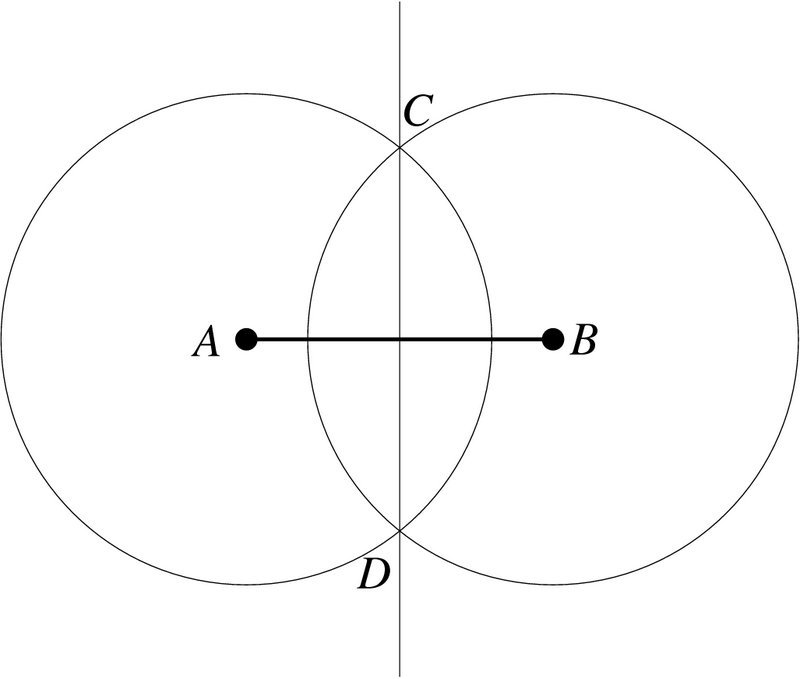
Έτσι, το μεσαίο σημείο του τμήματος βρέθηκε, τώρα δεν θα βλάψει να αποδείξει ότι είναι CD - το μεσαίο κάθετο και μοιράζεται το τμήμα στο μισό. Είναι εύκολο να το κάνεις. Μετά από όλα, δύο κύκλοι που σχηματίζουν μια γραμμή έχουν την ίδια ακτίνα, διάμετρο. Και σε κύκλους, όλα τα σημεία στη γραμμή απομακρύνονται εξίσου από το κέντρο της. Έτσι, τα σημεία C και D βρίσκονται επίσης στις ίδιες αποστάσεις από τα σημεία Α και Β. Η γραμμή που συνδέει τα σημεία D και C μπορεί να είναι μόνο ένα στο επίπεδο. Και το σημείο διασταύρωσης στο τμήμα βρίσκεται στην ίδια απόσταση. Όλα αυτά έπρεπε να διευκρινιστούν.





