Как вычислить площадь ромба?

В этой статье вы узнаете, как можно найти площадь ромба различными методами. Благодаря этим формулам будет легко решать задачи по геометрии, ведь здесь в статье будет описано, как вычислить площадь ромба, зная величину диагонали большей и меньшей, стороны, углы и диаметр вписанной окружности в ромб.

Узнать площадь ромба можно по разным формулам. Достаточно знать свойства это фигуры и свойства других фигур, ведь ромб можно разбить на треугольники, приравнять его к параллелограмму и т.п. Ниже вы увидите такие формулы. Еще необходимо знать, чем отличается ромб от четырехугольника и параллелограмма. По математическому определению. Ромб представляет собой фигуру подобную параллелограмму с равными сторонами, но в отличие от квадрата – у ромба углы не прямые. Зато сумма двух углов у основания ромба будет равняться 180 градусов. Все эти знания пригодятся для расчета площади ромба, далее подробнее.

Как вычислить площадь ромба – свойства фигуры

Прежде, чем вычислить площадь ромба, лучше ознакомиться со свойствами данной фигуры. Ведь благодаря знанию этих характеристик дальше проще будет доказать вероятность той или иной формулы. Ранее упоминалось уже, что такое ромб. Он представляет собой фигуру с равными абсолютно всеми сторонами, равными противоположными острыми и тупыми углами, но не прямыми.

Ромб имеет следующие свойства:

• у него все стороны между собой равны
• углы, лежащие напротив друг друга, тоже равны
• диагонали данной фигуры являются биссектрисами, в точке пересечения делятся на равные отрезки
• также диагонали пересекаются в центре ромба и под прямыми углами
• противоположные стороны фигуры не могут пересекаться, даже если продлить лучи они же параллельны, как у параллелограмма.

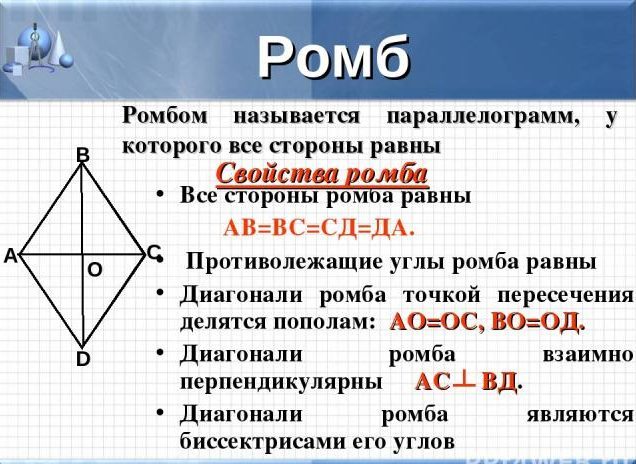
ВАЖНО: Обратите внимание, что ромб можно разбить на четыре прямоугольных треугольника, которые будут между собой равны по площади, или на два равносторонних идентичных треугольника, см. изображение выше.

Как вычислить площадь ромба?

Итак, давайте выясним, как вычисляется площадь ромба. Давайте воспользуемся для этого формулой площади прямоугольника, где:

• S = a • b, где a, b – стороны прямоугольника.

Чтобы было понятно, как вывести из этой формулы, формулу площади ромба, смотрите объяснение:

1. Нарисуйте ромб, проведите высоту к основанию ромба BH.
2. Из точки D на линию AD проведите тоже высоту CH1.
3. Выходит что треугольник ABH и треугольник CH1D между собой равны по двум общим сторонам, ∠ углу между ними.
4. Значит AH=DH1. Площадь образовавшегося квадрата будет равна площади ромба
5. А значит BH • HH1 – это и есть площадь ромба, другими словами произведение высоты BH ромба на сторону AD и будет S площадью ромба, поскольку HH1 = BC, а BH – это высота.

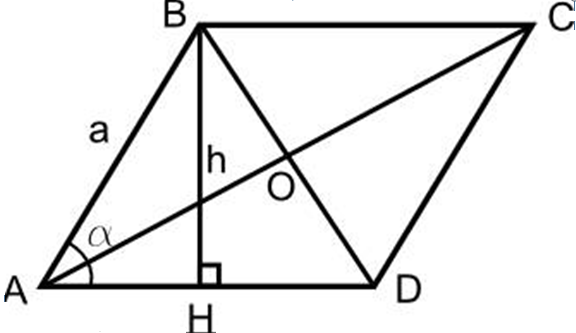
Из доказательства вытекает, что:

• S ромба = a • h и измеряется в квадратных единицах.

Как найти площадь ромба, зная угол и сторону геометрической фигуры?

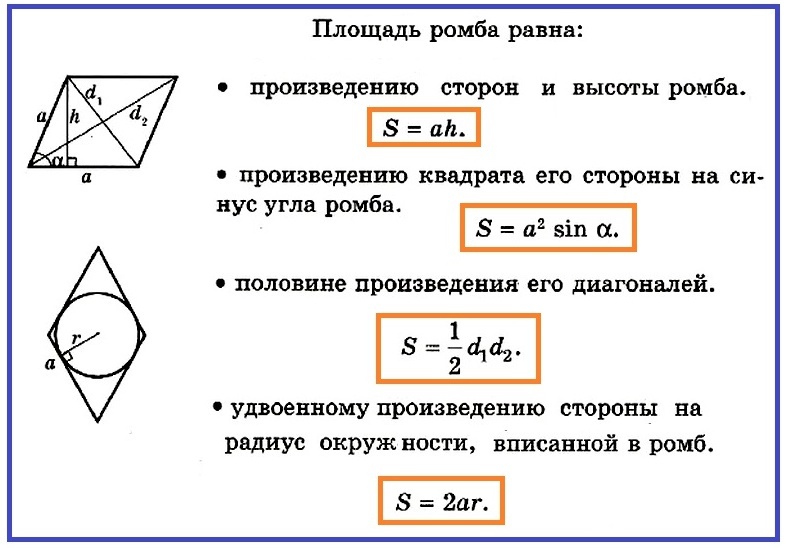
Теперь мы знаем, как выглядит формула площади ромба, можем по этой же формуле найти и S площадь ромба, зная чему равна сторона ромба и ∠ угол, например, острый у основания, как на фото ниже.

• S = a • h

Но в нашем случае нам неизвестна высота ромба, ее следует найти. Для этого придется рассмотреть треугольник прямоугольный, который получился, когда была проведена высота к основанию ромба.

В этом треугольнике известна гипотенуза и ∠α. Чтобы вычислить площадь всей фигуры, понадобится найти высоту. А h = a • sin∠α.  Значит S площадь равностороннего параллелограмма (ромба) равняется:

• S = a • a • sin∠α = a² • sin∠α

Как вычислять площадь ромба, зная его диагонали?

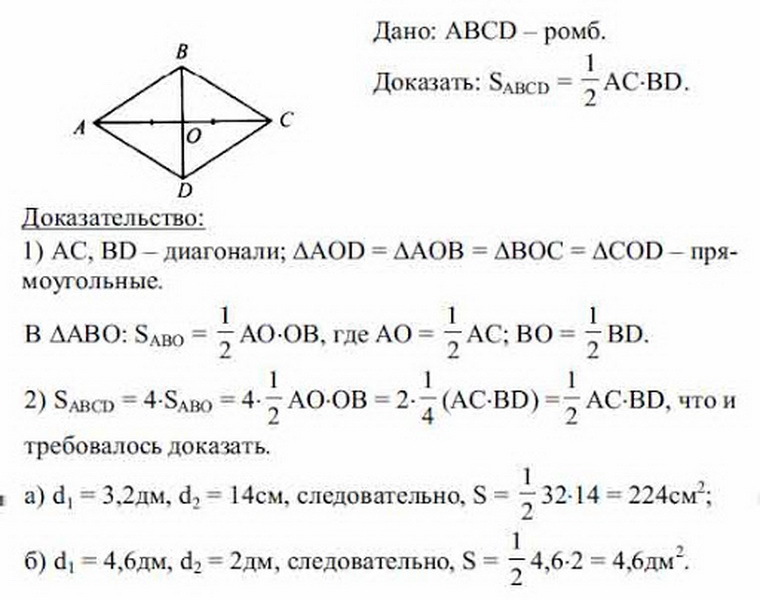
Чтобы узнать формулу площади ромба, когда известны только (a, b) диагонали, следует рассмотреть следующий пример. Дано BCDA – ромб и знаем чему равны диагонали. Теперь следует найти S площадь равностороннего параллелограмма по величинам диагоналей.

Ранее уже рассматривали свойства ромба. Диагонали ромба равны, в точке пересечения делятся на равные отрезки. Из этого следует, что все треугольники, которые вписаны в фигуру в результате пересечения обеих диагоналей тоже равны между собой и они прямоугольные (по трем сторонам). Чтобы найти площадь ромба, достаточно найти площадь одного треугольника и полученные данные умножить на 4.

Итого выходит, что:

• S ромба = 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) = 4 • 1/8 AC • BD = 1/2 BD • AC, итого площадь S ромба будет = произведению a • b (диагоналей) деленное на два: S = 1/2 a • b

Как вычислять площадь ромба, зная его сторону и радиус вписанной в него окружности?

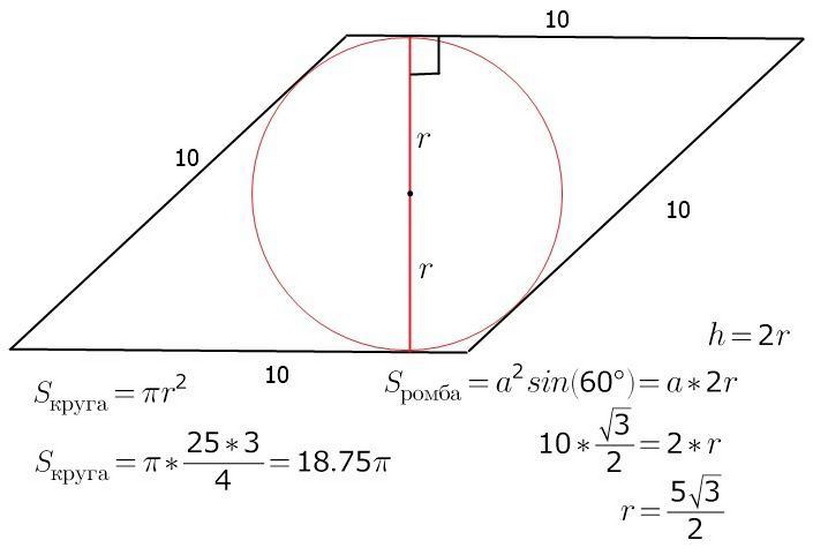
Площадь ромба можно рассчитать, зная r – радиус и a – длину стороны фигуры. Уже известно, что S – площадь фигуры будет равна произведению b – стороны на h – высоту. Через центр окружности, он же будет являться и центром пересечения a, b – диагоналей ромба. Проведите высоту и одновременно диаметр ромба. На изображении видно, что высота фигуры – это два радиуса окружности. Теперь легко будет найти и площадь самого ромба:

• S = a • h = a • 2r

Ниже смотрите пример задачи на данную тематику.

Еще смотрите подобные статьи на данную тематику здесь:

1. Площадь прямоугольника, как найти?
2. Как найти площадь круга?
3. Площадь квадрата – формулы.

Видео: Пример того, как вычислять площадь ромба