Як знайти квадратну площу, якщо периметр відомий, діагональ? Як знайти квадрат квадрата, вписаного в колі, і описано поблизу окружності: формула, приклади вирішення проблем. Як знайти сторону та діагоналі квадрата, якщо його область відома?

Прочитайте статтю, щоб знати, як знайти квадратну область по -різному.

Квадрат - рівносторонній прямокутник. Цей належний і плоский чотирикутник має рівність у всіх сторонах, куточках та діагоналі. Через те, що існує така рівність, формула обчислення області та інших характеристик дещо модифікована порівняно з іншими математичними показниками. Але це не робить завдання занадто складними. Давайте проаналізуємо всі формули та рішення цієї статті.

Як знайти сторону квадрата, знаючи її територію?

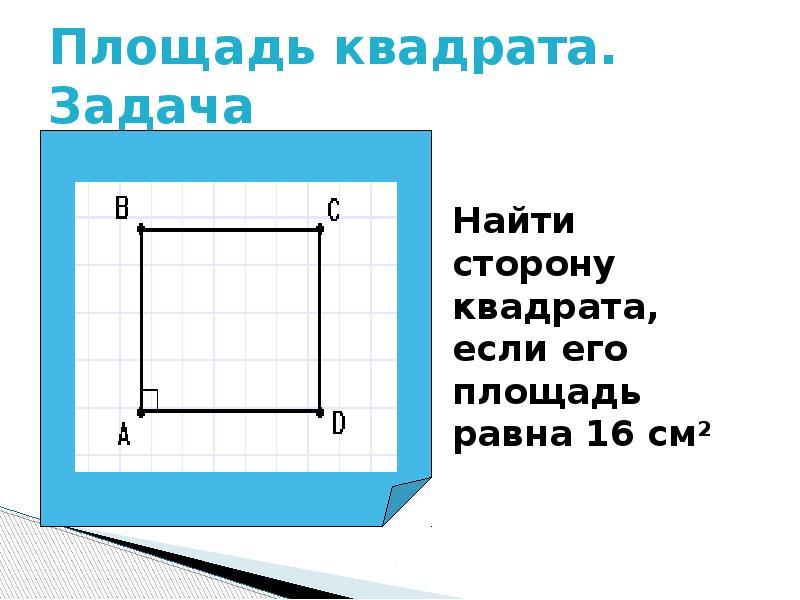
Майдан С. Прямі та квадратні квадрати обчислюються формулою: помножити на б.. Але оскільки квадрат має повну рівність сторін, його площа буде рівною: S \u003d (a) у другому ступені.  Як з’ясувати розмір сторони квадрата, знаючи його область?

• Якщо відома площа квадратного квадрата, то ми знаходимо сторону, обчислюючи площу з -під квадратного кореня.
• Наприклад, площа квадрата становить 49, то що дорівнює стороні?
• 49 \u003d (a) у другому ступені. Рішення: a \u003d корінь 49 \u003d 7. Відповідь: 7.

Якщо вам потрібно знайти сторону квадратного квадрата, область якої занадто довга, тоді використовуйте калькулятор. Спочатку наберіть номер області, а потім натисніть root Sign на клавіатурі калькулятора. Отримане число буде відповіддю.

Як знайти квадратний діагональ, якщо його область відома?

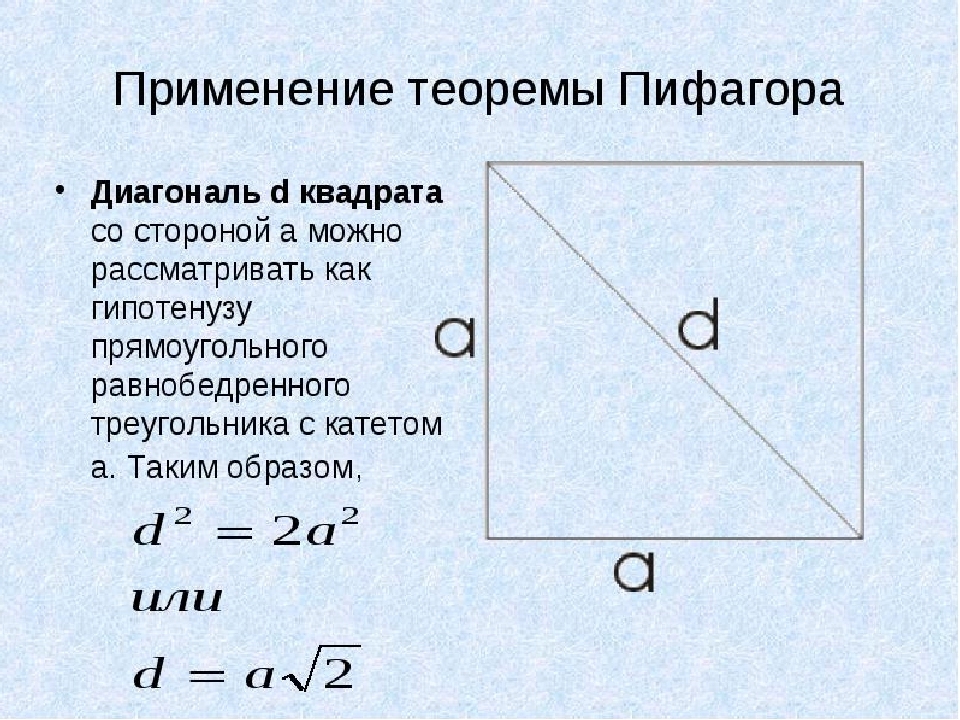
У цьому прикладі ми будемо використовувати теорему Піфагора. У квадраті всі сторони рівні, а діагональ d. Ми розглянемо як гіпотенузу прямокутного трикутника ізобей з ногою . Тепер ми знаходимо квадратну діагональ, якщо відома його область:

• Для того, щоб не намалювати всю теорему Піфагора, ми вирішимо другий варіант: d \u003d aising, де a - сторона квадрата.
• Отже, ми знаємо площу квадрата, наприклад, вона дорівнює 64. Отже, одна сторона a \u003d √64 \u003d 8.
• Виявляється D \u003d 8√2. Корінь 2 не виходить усього числа, тому у відповіді ви можете написати так: d \u003d 8√2. Але, якщо ви хочете обчислити значення, тоді використовуйте калькулятор: √2 \u003d 1,41421356237 і помножте на 8, виявляється 11, 3137084.

Важливо: Зазвичай у математиці не залишається чисел з великою кількістю чисел. Потрібно круглі або залишати з коренем. Тому відповідь на діагоналі полягає в тому, якщо область становить 64 наступним чином: d \u003d 8√2.

Як знайти квадратну площу через діагональ?

Формула пошуку квадратної області через діагональ проста:

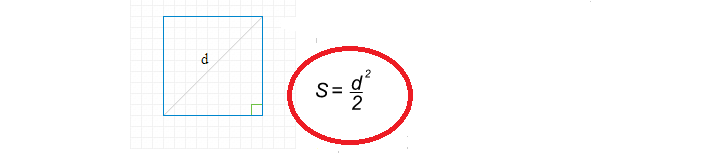
Тепер напишемо рішення, щоб знайти квадратну ділянку через діагональ:

• Діагональ d \u003d 8.
• 8 на площі 64.
• 64 Розділіть на 2 рівні 32.
• Квадратна площа - 32.

Порада: Це завдання має ще одне рішення через теорему Піфагора, але воно є складнішим. Тому використовуйте рішення, яке ми вивчали.

Як знайти квадратну площу, знаючи її периметр?

Периметр квадратного квадрата П. - Це сума всіх сторін. Щоб знайти свою область, знаючи його периметр, спочатку потрібно обчислити сторону квадратного квадрата. Рішення:

• Припустимо, периметр становить 24. Розділіть 24 на 4 сторони, виявляється 6 - це одна сторона.
• Тепер ми використовуємо формулу для пошуку області, знаючи, якою сторона квадратного квадрата дорівнює: S \u003d a в квадраті, s \u003d 6 у квадраті \u003d 36.
• Відповідь: 36

Як бачите, знаючи периметр площі, просто знайдіть його область.

Як знайти площу квадрата, вписаного в колі з заданим радіусом?

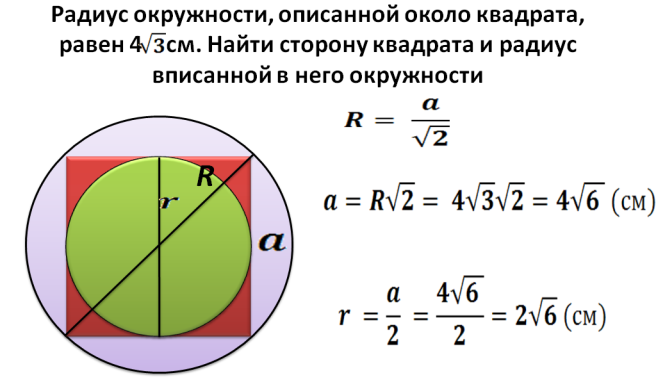
Радіус R - Це половина діагоналі квадрата, вписаного по колу. Тепер ми можемо знайти діагональ за формулою: d \u003d 2*r. Далі ми знаходимо квадрат квадрата, вписаний у колі з заданим радіусом:

• Діагональ - 2 множення на радіус. Наприклад, радіус дорівнює 5, тоді діагональ дорівнює 2*5=10.
• Це було описано вище, як знайти квадрат квадрата, якщо відомо діагональ: S \u003d діагональ у квадраті, розділеному на 2. s \u003d 10*10 і розділіть на 2 \u003d 50.
• Відповідь - 50.

Це завдання трохи складніше, але також легко вирішене, якщо ви знаєте всі формули.

Як знайти площу квадрата, описаний біля кола з заданим радіусом?

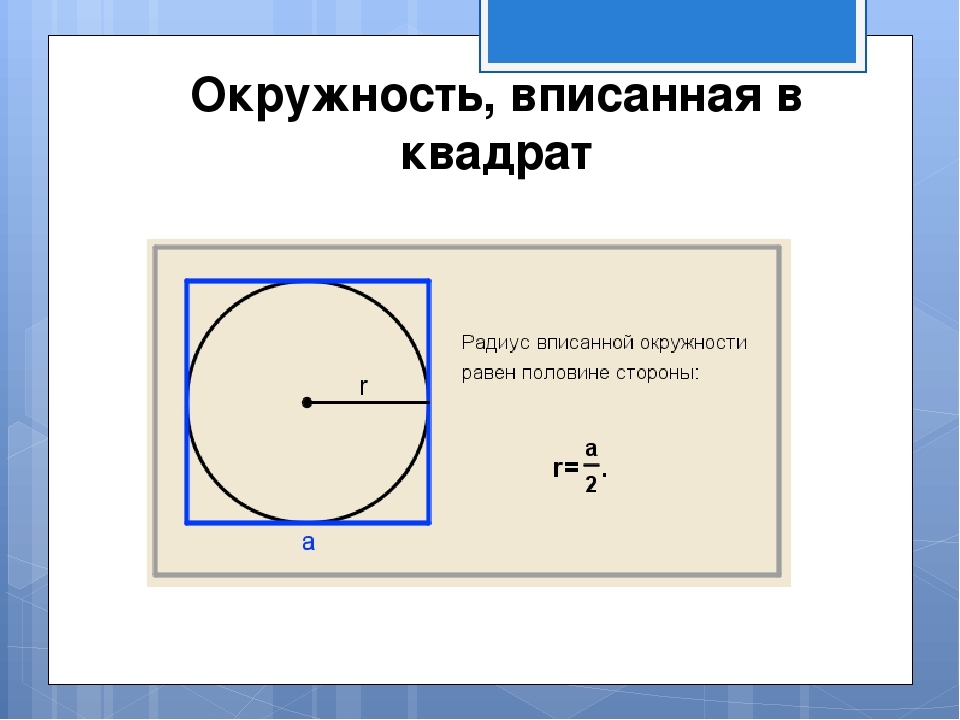
На малюнку видно, що радіус вписаного кола дорівнює половині сторони. Сторона розташована відповідно до зворотної формули, яка зображена на малюнку: a \u003d 2*r. Потім ми знаходимо площу квадрата, описану біля кола, із заданим радіусом відповідно до формули S \u003d і в квадраті. Рішення:

• Припустимо, радіус дорівнює 7. сторона квадрата A 2*7 \u003d 14.
• S \u003d 14 у квадраті \u003d 196.

Якщо ви розумієте суть вирішення таких проблем, то ви можете їх швидко і просто вирішити. Давайте розглянемо ще кілька прикладів.

Приклади вирішення проблем на тему "квадратний квадрат"

Щоб виправити матеріал, охоплений і запам'ятайте всі формули, необхідно вирішити кілька прикладів проблем на тему "квадратної області". Ми починаємо з простого завдання і переходимо до вирішення більш складного:

Тепер ви знаєте, як використовувати формулу для квадрата квадрата, а це означає, що ви можете виконати будь -яке завдання. Успіх у майбутньому навчанні!

Відео: Обчислення квадратної області