Çevre biliniyorsa, diyagonal bir alan nasıl bulunur? Çembere yazılan ve çevrenin yakınında tarif edilen karenin karesinin nasıl bulunacağı: formül, problemleri çözme örnekleri. Eğer alanı biliniyorsa, meydanın tarafını ve diyagonalini nasıl bulabilirim?

Kare alanı farklı şekillerde nasıl bulacağınızı öğrenmek için makaleyi okuyun.

Kare eşkenar bir dikdörtgendir. Bu uygun ve düz dörtgen, her tarafta, köşede ve diyagonallerde eşitliğe sahiptir. Böyle bir eşitlik olması nedeniyle, alanı ve diğer özellikleri hesaplamak için formül, diğer matematiksel figürlere kıyasla biraz değiştirilmiştir. Ancak bu görevleri çok karmaşık hale getirmez. Bu makalenin tüm formüllerini ve çözümlerini analiz edelim.

Alanını bilerek meydanın tarafını nasıl bulabilirim?

Meydan S. Doğrudan ve kare kareler formülle hesaplanır: a Çarpmak b.. Ancak Meydan'ın tarafların tam bir eşitliğine sahip olduğundan, alanı eşit olacaktır: S \u003d (a) ikinci derecede.  Alanını bilerek, meydanın tarafının boyutunu nasıl bulabilirim?

• Kare kare alanı biliniyorsa, kare kökün altındaki alanı hesaplayarak tarafı buluruz.
• Örneğin, meydanın alanı 49'dur, o zaman tarafı eşittir?
• 49 \u003d (a) ikinci derecede. Çözüm: a \u003d 49 kökü \u003d 7. Cevap: 7.

Alanı çok uzun olan karenin tarafını bulmanız gerekiyorsa, hesap makinesini kullanın. Önce alanın sayısını arayın ve ardından hesap makinesi klavyesindeki kök işaretine basın. Ortaya çıkan numara cevap olacaktır.

Alanı biliniyorsa, kare diyagonal nasıl bulunur?

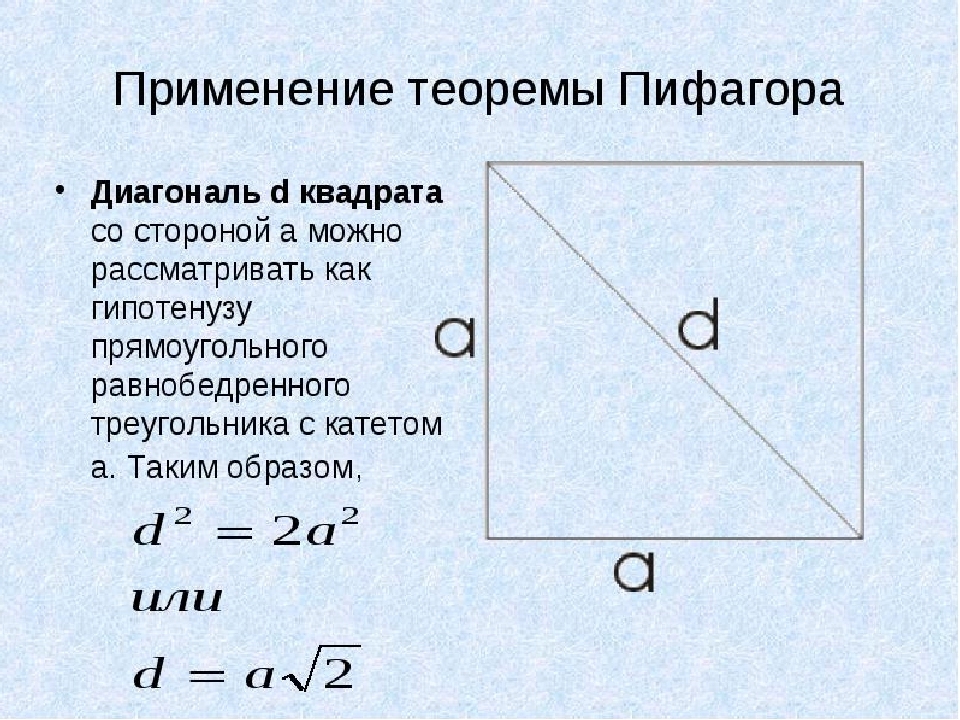
Bu örnekte, Pisagor teoremini kullanacağız. Bir karede, tüm taraflar eşittir ve diyagonal d. Dikdörtgen bir ikizkenar üçgenin bir bacak ile hipotenuse olarak değerlendireceğiz. a. Şimdi alanı biliniyorsa kare bir diyagonal buluyoruz:

• Tüm Pisagor teoremini boyamamak için ikinci seçeneğe karar vereceğiz: d \u003d AISION, burada A, meydanın tarafıdır.
• Yani, karenin alanını biliyoruz, örneğin, 64'e eşittir. a \u003d √64 \u003d 8.
• Ortaya çıkıyor D \u003d 8√2. 2'nin kökü tüm numarayı ortaya çıkarmaz, bu nedenle cevapta bu şekilde yazabilirsiniz: d \u003d 8√2. Ancak, değeri hesaplamak istiyorsanız, hesap makinesini kullanın: √2 \u003d 1.41421356237 ve 8 ile çarpın, 11, 3137084.

Önemli: Tipik olarak, matematikte, yanıt olarak çok sayıda sayıya sahip hiçbir sayı kalmaz. Kökle yuvarlamak veya bırakmak gerekir. Bu nedenle, diyagonalin cevabı, alanın aşağıdaki gibi 64 olmasıdır: d \u003d 8√2.

Diyagonal yoluyla kare bir alan nasıl bulunur?

Diyagonal boyunca kare alanı bulma formülü basittir:

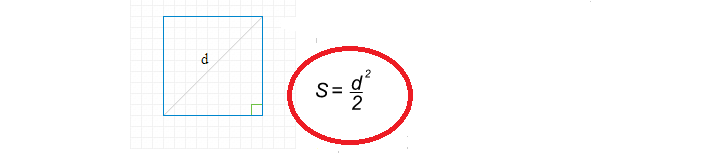
Şimdi diyagonal boyunca kare alanı bulmak için bir çözüm yazalım:

• Diyagonal d \u003d 8.
• Meydanda 8 64.
• 64 Eşit 32'ye bölün.
• Kare alan 32'dir.

Tavsiye: Bu görevin Pisagor teoreminden başka bir çözümü var, ancak daha karmaşık. Bu nedenle, incelediğimiz çözümü kullanın.

Çevresini bilerek kare bir alan nasıl bulunur?

Karenin çevresi P. - Bu tüm tarafların toplamıdır. Alanını bulmak için, çevresini bilerek, önce karenin tarafını hesaplamanız gerekir. Çözüm:

• Diyelim ki çevrenin 24 olduğunu varsayalım. 24'ü 4 tarafa bölün, 6 ortaya çıkıyor - bu bir taraf.
• Şimdi, kare karenin tarafının neye eşit olduğunu bilerek alanı bulmak için formülü kullanıyoruz: S \u003d a kare içinde, s \u003d 6 kare \u003d 36.
• Cevap: 36

Gördüğünüz gibi, meydanın çevresini bilmek, sadece alanını bulun.

Belirli bir yarıçapa sahip bir daireye yazılmış bir kare alanı nasıl bulunur?

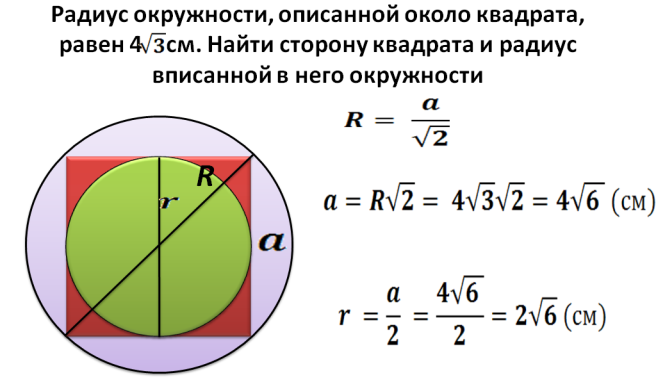
Yarıçap R - Bu, bir daireye yazılmış bir karenin diyagonalinin yarısıdır. Şimdi formülle bir diyagonal bulabiliriz: d \u003d 2*r. Ardından, belirli bir yarıçapa sahip bir daireye yazılmış karenin meydanını buluyoruz:

• Diyagonal yarıçapla 2 çarpılır. Örneğin, yarıçap 5'tir, sonra diyagonal eşittir 2*5=10.
• Diyagonal biliniyorsa, karenin karesinin nasıl bulunacağı yukarıda açıklanmıştır: S \u003d 2'ye bölünmüş bir karede diyagonal ve 2 \u003d 50'ye bölün.
• Cevap - 50.

Bu görev biraz daha karmaşıktır, ancak tüm formülleri biliyorsanız da kolayca çözülebilir.

Belirli bir yarıçapa sahip bir dairenin yakınında tarif edilen bir kare alanı nasıl bulunur?

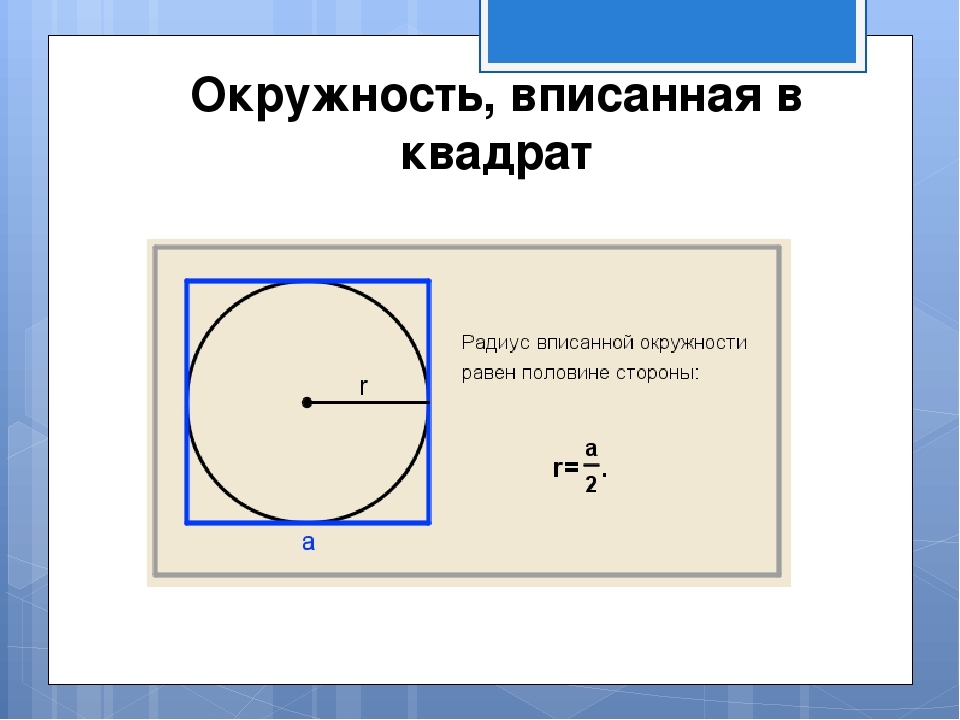
Resim, yazılı dairenin yarıçapının tarafın yarısına eşit olduğunu gösteriyor. Yan, resimde tasvir edilen ters formüle göre bulunur: a \u003d 2*R. Sonra, formüle göre belirli bir yarıçapla dairenin yakınında tarif edilen meydanın alanını buluyoruz. S \u003d ve bir karede. Çözüm:

• Yarıçapın 7 olduğunu varsayalım. A karısının tarafı 2*7 \u003d 14'tür.
• S \u003d 14 kare \u003d 196.

Bu tür sorunları çözmenin özünü anlarsanız, bunları hızlı ve basit bir şekilde çözebilirsiniz. Birkaç örnek daha bakalım.

"Kare" konusundaki sorunları çözme örnekleri

Kapsanan materyali sabitlemek ve tüm formülleri hatırlamak için, “kare alan” temasıyla ilgili birkaç sorun örneğini çözmek gerekir. Basit bir görevle başlıyoruz ve daha karmaşık çözmeye geçiyoruz:

Artık formülün karenin karesi için nasıl kullanılacağını biliyorsunuz, yani herhangi bir görev yapabileceğiniz anlamına geliyor. Gelecek eğitimde başarı!

Video: kare alanın hesaplanması