Како саставити коцку јакне корак по корак: упутства за почетнике и децу. Како саставити 3к3 рубик коцку: најлакши, најједноставнији и најбржи начин, шема

Позната слагалица, која је неколико сектора у боји, уједињена у једној коцки, појавила се 1974. године. Мађарски вајар и наставник одлучили су да створе уџбенику да би објаснили групну теорију студентима. До данас, ова играчка се сматра најбољем продати широм света.

Али, успех овој слагалици дошао је тек када је немачки предузетник Тибор Лакси обратио пажњу на то. Он је заједно са проналазачем Игара Том Цремер основао не само ослобађање коцкица, већ је организовао и напредак ове слагалице до маса. Захваљујући им да су се појавиле такмичења у Скупштини коцкица Рубик.

Успут, људи који су ангажовани у таквој монтирању ове слагалице називају се СпеедКуберс ("Спеед" - брзина). Није тешко погодити да се високо -Спеед Скупштина "Чаробне" коцка се назива брзином -јингинг.

Структура коцке чипа и назив ротације

Да бисте сазнали како да прикупите ову слагалицу, морате да разумете његову структуру и сазнајте тачно име одређених радњи. Потоњи је важан ако ћете пронаћи упутства за састављање коцке на Интернету. Да, и у нашем чланку назваћемо све акције са овом слагалицом, у складу са утврђеним изразима.

Стандардна гумена коцка састоји се од три стране. Од којих се свака састоји од три дела. Данас постоје и 5к5к5 коцкице. Класична коцка има 12 ребара и 8 углова. Осликано је у 6 боја. Унутар ове слагалице је крст, око којих се креће бочних страна крећу.

На крају крста, квадрат са једном од шест боја је ригидно смештено. Око тога, морате да сакупите остатак квадрата исте боје. Штавише, загонетка се сматра прикупљањем ако се на све шест страна коцке прикупља његова боја.

Важно: у оригиналној слагалици, жута боја је увек насупрот бело, наранџасто - црвено и зелено - плаво. А ако растављате слагалицу, а затим је погрешно преклопите, то може довести до чињенице да се никада не може прикупити.

Поред центара коцке, сталне компоненте ове загонетке су углови. Сваки од осам углова састоји се од три боје. И без обзира на то како мењате положај боја у овој слагалици, састав боја углова у њему се неће променити.

Важно: Рубика коцка се прикупља стављањем углова и средњих сектора у складу са бојама централних сектора.

Сада, када смо схватили, дизајн ове слагалице је време да пређе на имена странака и ротације и њихово именовање у специјализованој литератури.

У процесу састављања Рубик Цубе-а, то може захтијевати не само кретање странака, већ и промене положаја овог објекта у простору. Стручњаци називају пресретања ових покрета. Ово се шематски приказује на следећи начин:

ВАЖНО: Ако у алгоритму скупштине коцке налазите, само је назначено писмо, а затим мењамо положај бочно у смеру казаљке на сату. Ако је након писма назначен знак апострофе "'", онда ротирамо бочну катеру у смеру супротном од казаљке на сату. Ако је након писма назначен број "2", то значи да се на боку треба да се ротира два пута. На пример, Д2 '- Двапут ротирамо доњу страну у смеру супротном смеру казаљке у смеру супротном смеру.

Једноставна и једноставна метода монтаже: упутства за децу и почетнике

Најзначајнија упутства за Скупштине за почетнике су следеће:

• У првој фази Скупштине ове популарне загонетке почињемо са десним крстом. То јест, са чињеницом да ће са сваке стране коцке боја ребра и центара бити иста.
• Да бисте то учинили, налазимо бели центар и беле ребра и сакупљамо крстове према у складу са шемом испод:

• Након горе наведених акција, морамо добити крст. Наравно, први пут када Крст неће бити тачан и не требате мало трансформисати резултирајућу опцију. Уз праве перформансе, то ће бити једноставно да промените ребра међу собом.
• Овај алгоритам се назива "ПИТ-ПАФ" и приказан је у дијаграму испод:

• Наставимо на следећи корак Скупштине загонетке. Бели угао налазимо на доњем слоју и ставимо црвени угао над њу. То се може учинити на различите начине, у зависности од положаја црвених и белих углова. Користимо горе описану ПИФ-ПАФА методу.

• Као резултат тога, требали бисмо бити следећи:

• Почињемо да сакупљамо други слој. Да бисмо то учинили, нађемо четири ребра без жуте и постављају их између центара другог слоја. Затим уврнемо коцка док се боја Центра поклапа са бојом елемента ивице.
• Као и код Скупштине претходног слоја, можда ће вам требати још неколико опција да бисте постигли овај циљ:

• Након што смо успешно завршили претходни корак, прелазимо на Скупштину Жутог крста. Понекад се он "скупља". Али то се дешава врло ретко. Најчешће, коцка у овој фази има три опције за локацију цвећа:

Дакле, жути крст је сакупљен. Даљње акције приликом решавања ове слагалице своди на седам опција. Испод се приказује свака од њих:

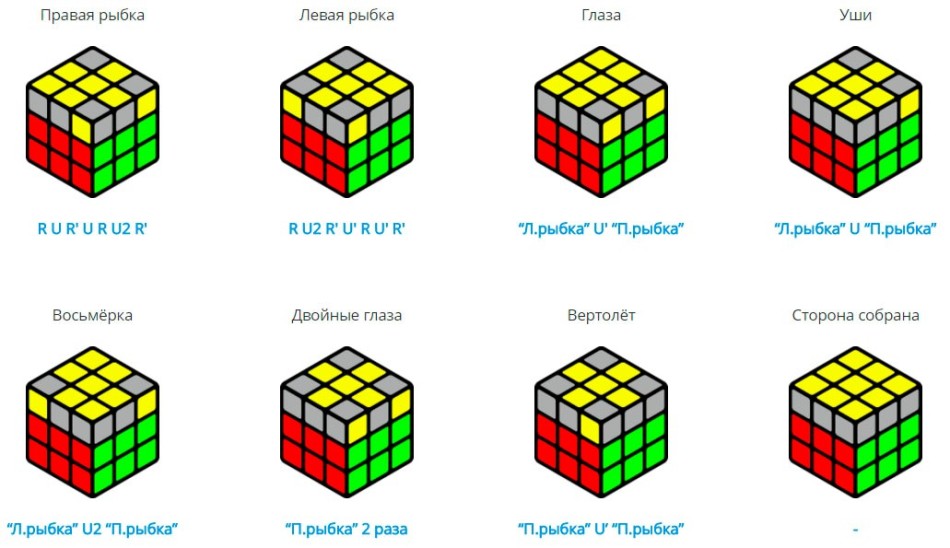
У следећем кораку морамо да сакупимо углове горњег слоја. Узмите један од углова и ставите га на место користећи У, У 'и У2 покрете. У овом случају морате узети у обзир. Тако да су боје угла идентичне боје на доњим слојевима. Када користите овај корак, држите коцку белу за себе.

• Завршна фаза склопа коцке је монтажа ребра горњег слоја. Ако сте исправно урадили све горе, онда се могу појавити четири ситуације. Они решавају врло једноставно:

Најбржи начин. Јессица Фриедрицх метода

Ова метода Скупштине загонетка развила је Јессица Фредерицк 1981. године. Концептуално се не разликује од већине познатих метода. Али, она наглашава прецизно на брзину монтаже. Због тога је број фаза Скупштине смањен од седам до четири. Да бисте савладали ову методу, морате савладати "Укупно" 119 алгоритама.

ВАЖНО: Ова техника није погодна за почетнике. Његова студија треба да се уради када ће ваша брзина монтаже коцке постати мање од 2 минута.

1. У првој фази морате да сакупите крст са бочним лицима. У специјализованој литератури, ова фаза се зове "Крст" (са енглеског крста - крст).

2. У другој фази морате одједном прикупити два слоја слагалице. Он се зове "Ф2Л" (са енглеског. Прва 2 слоја - прва два слоја). Следећи алгоритми ће можда бити потребни да би се постигао резултат:

3. Сада морате потпуно да сакупите горњи слој. Не треба да обраћате пажњу на бочне стране. Назив позорнице је (са енглеског језика. Оријентација последњег слоја - оријентација последњег слоја). За монтажу, морате да научите 57 алгоритма:

4. Завршна фаза склопа коцке. ПЛЛ (са енглеског језика. Пермутација последњег слоја - распоред елемената последњег слоја на местима). Скупштина се може извести користећи следеће алгоритме:

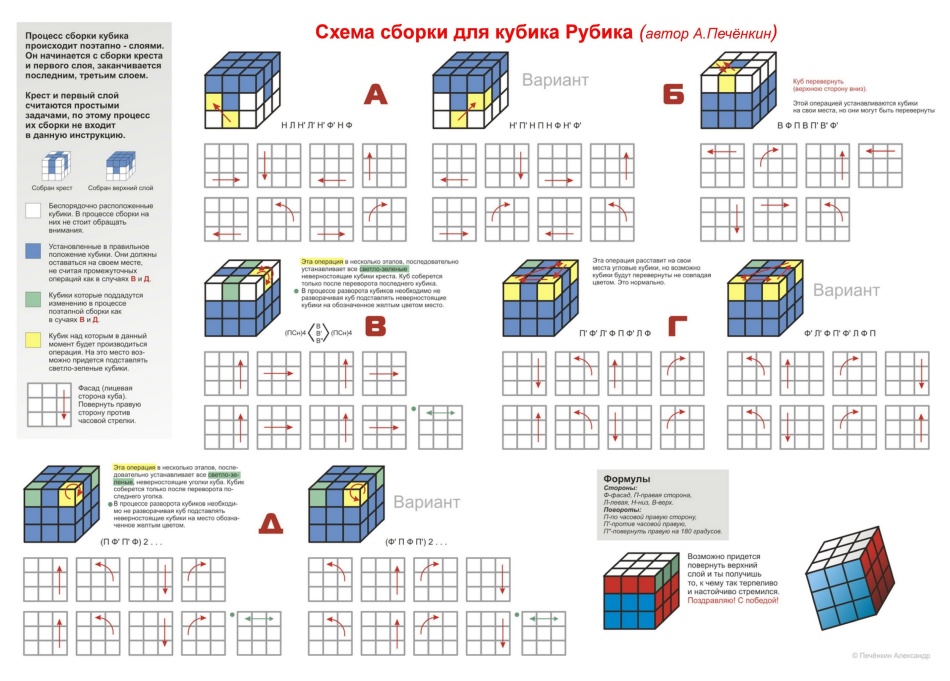
САСТАВНА СХЕМА 3КС3 ЦХУББИ ЦУБЕ у 15 потеза

Од 1982. године, када се појавио конкуренција за високо-најповољније склоп рубик коцка, многи љубитељи ове слагалице почели су да развијају алгоритме који би помогли да правилно договорите сектор коцке са минимумом кретања. Данас се зове минимални број потеза у овој слагалици "Алгоритам Бога" И износи 20 потеза.

Стога, за 15 потеза не можете да сакупите коцку чипа. Штавише, пре неколико година је развијен 18-годишњи алгоритам за састављање ове слагалице. Али, то се не може користити од свих одредби коцке, па је одбијен као најбрже.

У 2010. години научници из Гооглеа створили су програм са којим су израчунали најбржи алгоритам за састављање Рубик коцке. Потврдио је да је минимални број корака 20. Касније, из детаља популарног дизајнера, створен је Робот ЛЕГО Миндсторм ЕВ3, што је способан да прикупи прогутајућа бубуља од било које положаја у 3.253 секунди. Он користи у свом "послу" ходању "Алгоритам Бога". А ако вам неко каже о чињеници да постоји схема склопа Цубе 15 корака, не верујте му. Чак су и Гоогле-ове капацитете "нестали" да би га пронашли.

Колико је лако сакупљати коцку рабика: видео