Како пронаћи квадратни простор ако је обод познат, дијагонални? Како пронаћи квадрат квадрата утемељен у круг и описан у близини обима: формула, примери решавања проблема. Како пронаћи бочну и дијагоналу квадрата, ако је познато његово подручје?

Прочитајте чланак да бисте знали како пронаћи квадратни простор на различите начине.

Садржај

Трг је једнакостранични правоугаоник. Ова правилна и равна четверокута има једнакост на свим странама, угловима и дијагоналима. Због чињенице да постоји таква равноправност, формула за израчунавање подручја и других карактеристика је благо модификована у поређењу са другим математичким личностима. Али то не чини задатке превише компликовано. Анализирајмо све формуле и решења овог члана.

Како пронаћи страну трга, знајући њено подручје?

Квадрат С. Директни и квадратни квадрат израчунавају се формула: а Помножити са б.. Али будући да трг има потпуну једнакост странака, његова површина ће бити једнака: С \u003d (а) у другом степену.Како сазнати величину бочне стране трга, знајући њено подручје?

Ако је познато подручје квадратног трга, онда нађемо страну израчунавањем подручја испод квадратног корена.
На пример, површина квадрата је 49, шта је онда једнако једнака?
49 \u003d (а) у другом степену. Решење: а \u003d корен од 49 \u003d 7. Одговор: 7.

Ако требате да пронађете бок квадратног трга, од којих је површина предуга, а затим користите калкулатор. Прво бирајте број подручја, а затим притисните коријенску знаку на тастатури калкулатора. Резултирајући број ће бити одговор.

Како пронаћи квадратну дијагоналу ако је познато његово подручје?

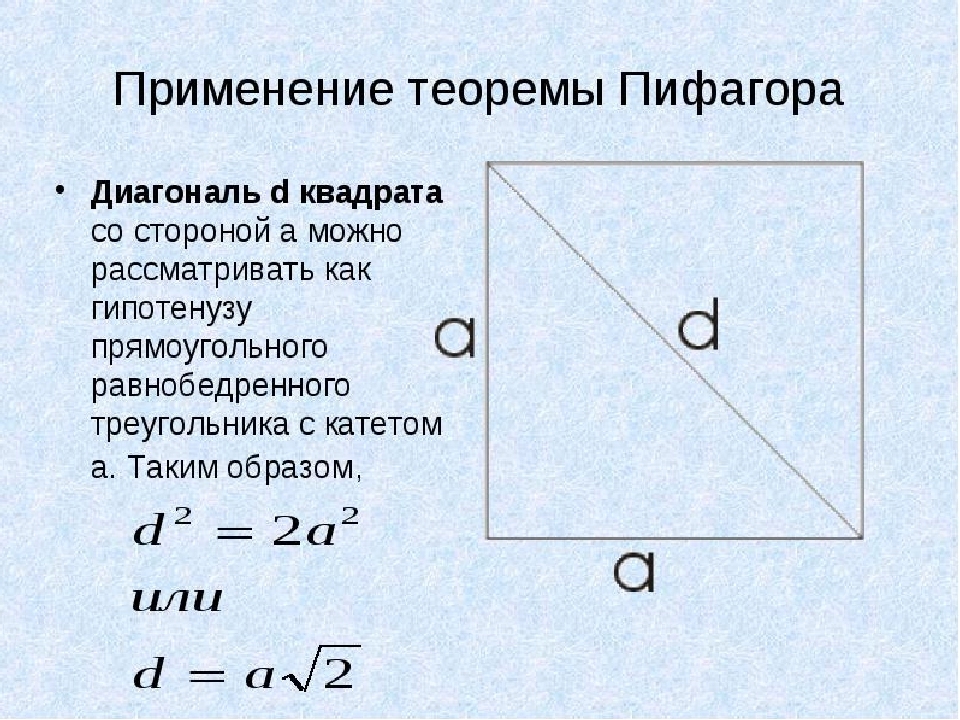
У овом примеру ћемо користити теорему Питагоре. На квадрату све стране су једнаке и дијагонале д. Размотрићемо као хипотенуза правоугаоног изосцела троугла са ногом а. Сада налазимо квадратну дијагоналу ако је познато његово подручје:

Да бисте не сликали целу питагорејску теоруму, одлучићемо о другој опцији: д \u003d Аисинг, где је а је страна квадрата.
Дакле, на пример, знамо подручје квадрата, то је једнако 64. па једна страна а \u003d √64 \u003d 8.
Испада Д \u003d 8√2. Корен 2 не испада цео број, па у одговору можете написати овај начин: д \u003d 8√2. Али, ако желите да израчунате вредност, користите калкулатор: √2 \u003d 1.41421356237 и помножите са 8, испада 11, 3137084.

Важно: Типично, у математици, ниједан број са великим бројем бројева није остављен у одговору. Потребно је да се окреће или одлази са кореном. Стога је одговор на дијагоналу ако је то подручје 64 на следећи начин: д \u003d 8√2.

Како пронаћи квадратни простор дијагоналом?

Формула за проналажење квадратног подручја кроз дијагоналу је једноставна:

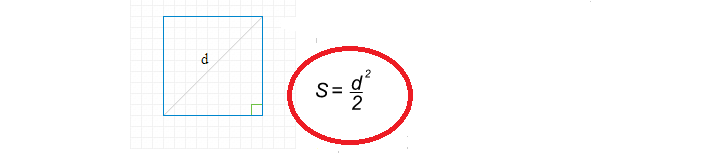
Сада да напишемо решење да пронађемо квадратни простор кроз дијагоналу:

Дијагонал Д \u003d 8.
8 на тргу је 64.
64 Поделите са 2 једнака 32.
Површина квадрата је 32.

Савет: Овај задатак има још једно решење путем Питагоре теорема, али је сложенији. Стога користите решење које смо испитали.

Како пронаћи квадратни простор, знајући његов обод?

Обод квадратног трга П. - Ово је збир свих странака. Да бисте пронашли њено подручје, знајући свој обод, прво морате израчунати бок квадратног трга. Решење:

Претпоставимо да је обод 24. Поделите 24 на 4 стране, испада 6 - ово је једна страна.
Сада користимо формулу за проналажење подручја, знајући шта је страна квадратног трга једнака: С \u003d а на квадрату, с \u003d 6 на квадрату \u003d 36.
Одговор: 36

Као што видите, знате обоглед квадрата, само пронађите њено подручје.

Како пронаћи подручје квадрата утјеченог у круг са датим радијусом?

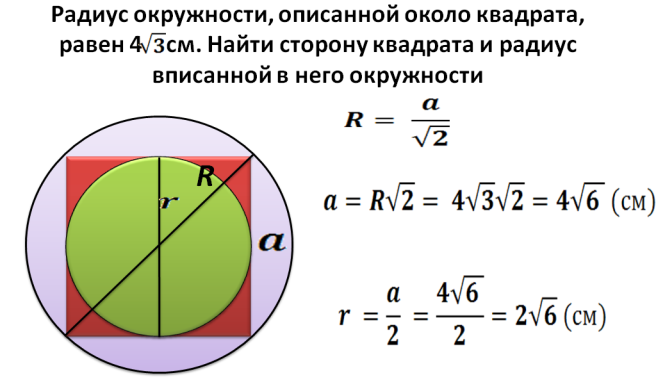
Радијус Р - Ово је половина дијагонале квадрата утјеченог у круг. Сада можемо пронаћи дијагоналу формуле: д \u003d 2 * р. Затим проналазимо квадрат квадрата утјеченог у круг са датим радијусом:

Дијагонала је 2 помноженост у радијусу. На пример, радијус је 5, а затим је дијагонала једнака 2*5=10.
Горе је описано како пронаћи квадрат квадрата ако је дијагонала позната: С \u003d дијагонала на квадрату подељеном у 2. С \u003d 10 * 10 и поделите са 2 \u003d 50.
Одговор - 50.

Овај задатак је мало сложенији, али и лако решени ако знате све формуле.

Како пронаћи површину квадрата описаног у близини круга са датим радијусом?

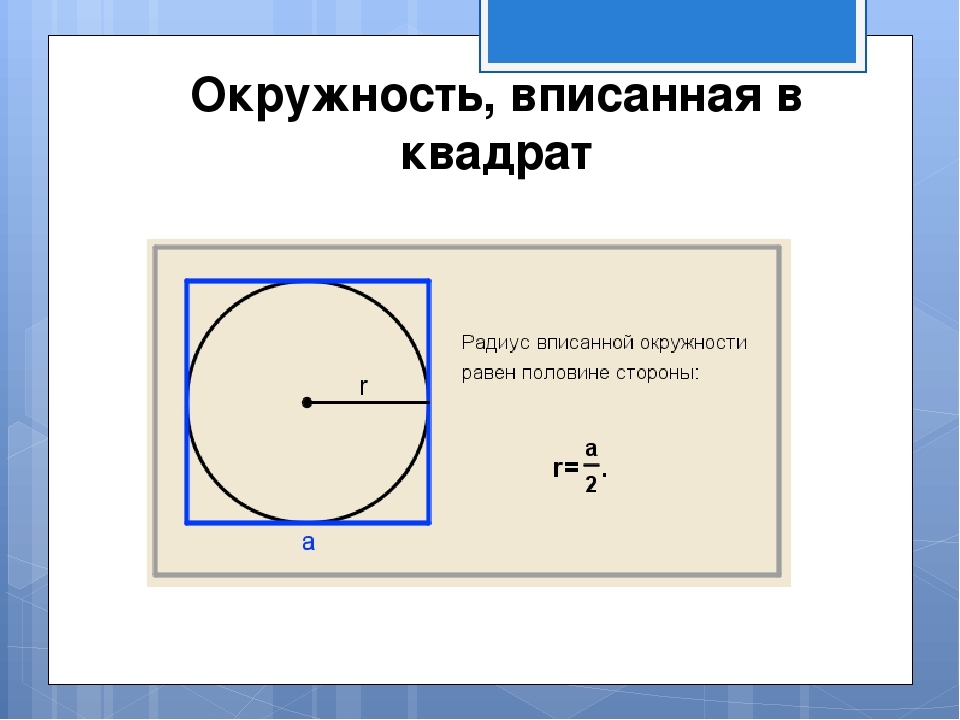
Слика показује да је полумјер уписаног круга једнак половини бочне стране. Страна се налази у складу са обрнутом формулом која је приказана на слици: а \u003d 2 * р. Затим нађемо подручје квадрата описаног у близини круга са датим радијусом према формули С \u003d и на квадрату. Решење:

Претпоставимо да је радијус 7. страна квадрата А је 2 * 7 \u003d 14.
С \u003d 14 на квадрату \u003d 196.

Ако разумете суштину решавања таквих проблема, онда их можете брзо и једноставно можете решити. Погледајмо још неколико примера.

Примери решавања проблема на теми "Скуаре Скуаре"

Да бисте исправили прекривени материјал и запамтите све формуле, потребно је решити неколико примера проблема на тему "квадратног подручја". Почињемо са једноставним задатком и прелазимо на решавање сложеније: