Kako rešiti gibe za gibanje? Formula odvisnosti med hitrostjo, časom in razdaljo. Naloge in rešitve.
Zadovoljstvo
- Formula za odvisnost časa, hitrosti in razdalje v 4. razredu: Kako je hitrost, čas, razdalja?
- Kako najti čas, poznavanje hitrosti in razdalje?
- Kako najti hitrost, če sta znana čas in razdalja?
- Kako najti razdaljo, če sta znana čas in hitrost?
- Graf hitrosti telesa na čas: fotografija
- Tabela 4 Razred: hitrost, čas, razdalja
- Primeri reševanja težav za hitrost, čas, razdaljo za 4. razred
- Video: Naloge gibanja
Formula za odvisnost časa, hitrosti in razdalje v 4. razredu: Kako je hitrost, čas, razdalja?
Ljudje, živali ali avtomobili se lahko premikajo z določeno hitrostjo. Za določen čas lahko gredo določeno pot. Na primer: danes lahko dosežete šolo čez pol ure. Greš z določeno hitrostjo in v 30 minutah premagaš 1000 metrov. Pot, ki se premaga, je v matematiki označena s pismom .. Hitrost je označena s pismom v. In čas, za katerega je bila pot zavrnjena, je označen s pismom t.
- Pot - .
- Hitrost- v
- Čas - t
Če zamujate v šolo, lahko v 20 minutah greste enako in povečate svojo hitrost. Torej, isto pot je mogoče potovati v različnih časih in pri različnih hitrostih.
Kako je čas prehoda odvisen od hitrosti?
Večja kot je hitrost, hitrejša bo razdalja. In nižja je hitrost, več časa morate prehoditi pot.

Kako najti čas, poznavanje hitrosti in razdalje?
Če želite najti čas, ki ga morate prenesti pot, morate vedeti razdaljo in hitrost. Če je razdalja razdeljena na hitrost, boste izvedeli čas. Primer takšne naloge:
Naloga zajca. Zajček je pobegnil od volka s hitrostjo 1 kilometer na minuto. Tekel je do luknje 3 kilometre. Za kdaj je zajček dosegel luknjo?

Kako je enostavno rešiti težave za gibanje, kjer morate najti razdaljo, čas ali hitrost?
- Previdno preberite nalogo in ugotovite, kaj je znano iz pogojev problema.
- Napišite te podatke na osnutek.
- Napišite tudi, kaj je neznano in kaj je treba najti
- Uporabite formulo za naloge o razdalji, času in hitrosti
- Vnesite znane podatke v formulo in rešite težavo
Rešitev za težavo o zajcu in volku.
- Iz pogojev problema ugotovimo, da poznamo hitrost in razdaljo.
- Prav tako iz pogojev problema ugotovimo, da moramo najti čas, ki ga potrebuje zajček, da doseže luknjo.

Na osnutek teh podatkov zapišemo na primer:
Razdalja do luknje - 3 kilometre
Hitrost zajca - 1 kilometer v 1 minuti
Čas ni znan
Zdaj pišemo enako kot matematični znaki:
. - 3 kilometre
V - 1 km/min
t — ?
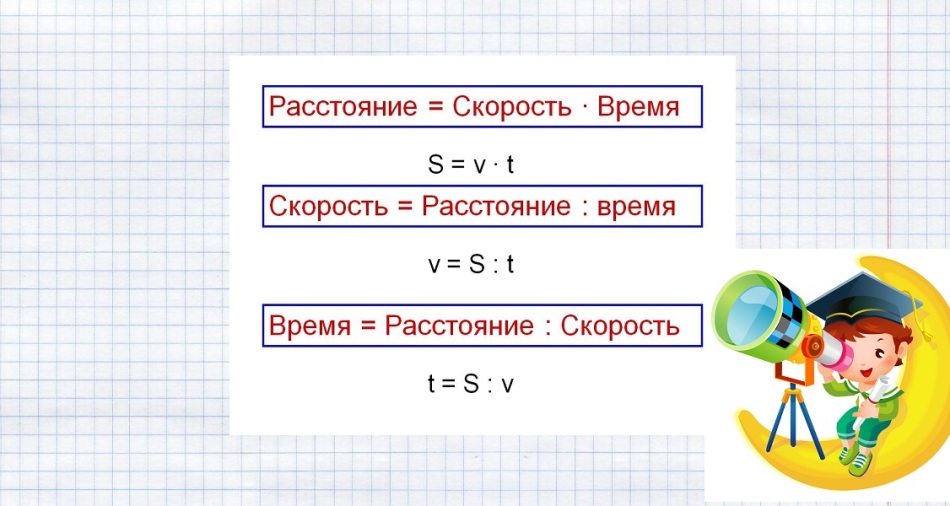
Spominjamo se in napišemo formulo, da bi našli čas v prenosniku:
t \u003d S: V
Zdaj zapišemo rešitev problema s številkami:
t \u003d 3: 1 \u003d 3 minute
Kako najti hitrost, če sta znana čas in razdalja?
Če želite najti hitrost, če sta čas in razdalja znana, je treba razdaljo nekaj časa razdeliti. Primer takšne naloge:
Zajček je pobegnil od volka in stekel do njegove luknje 3 kilometre. To razdaljo je premagal v 3 minutah. S kakšno hitrostjo je tekel zajček?
Reševanje problema gibanja:
- V osnutku zapišemo, da poznamo razdaljo in čas.
- Iz pogojev problema določimo, kaj je treba najti
- Ne pozabite na formulo za iskanje hitrosti.
Formule za reševanje takšnih težav so prikazane na spodnji sliki.
Nadomestimo znane podatke in rešimo težavo:
Razdalja do luknje - 3 kilometre
Čas, za katerega je zajček dosegel luknjo, je 3 minute
Hitrost ni znana
Te znane podatke pišemo z matematičnimi znaki
. - 3 kilometre
t - 3 minute
v -?
Zabeležite formulo, da najdete hitrost
v \u003d s: t
Zdaj zapišemo rešitev problema s številkami:
v \u003d 3: 3 \u003d 1 km/min

Kako najti razdaljo, če sta znana čas in hitrost?
Če najdete razdaljo, če je znan čas in hitrost, je treba pomnožiti hitrost. Primer takšne naloge:
Zajček je pobegnil od volka s hitrostjo 1 kilometer v 1 minuti. Tri minute je trajalo, da je tekel do luknje. Kakšno razdaljo je tekel zajček?
Rešitev problema: pišemo na osnutek, ki ga poznamo iz pogojev problema:
Hitrost zajca - 1 kilometer v 1 minuti
Čas, ko je zajček zbežal v Noro, je 3 minute
Razdalja ni znana
Zdaj bomo isto napisali z matematičnimi znaki:
v - 1 km/min
t - 3 minute
S -?
Ne pozabite na formulo za iskanje razdalje:
S \u003d v ⋅ t
Zdaj zapišemo rešitev problema s številkami:
S \u003d 3 ⋅ 1 \u003d 3 km

Kako se naučiti rešiti bolj zapletene težave?
Če želite izvedeti, kako rešiti bolj zapletene naloge, morate razumeti, kako preproste naloge so rešene, ne pozabite, kateri znaki kažejo na razdaljo, hitrost in čas. Če se ni mogoče spomniti matematičnih formul, jih je treba zapisati na list papirja in vedno imeti pri roki med reševanjem težav. S svojim otrokom rešite preproste naloge, ki jih je mogoče izumiti na poti, na primer med sprehodom.

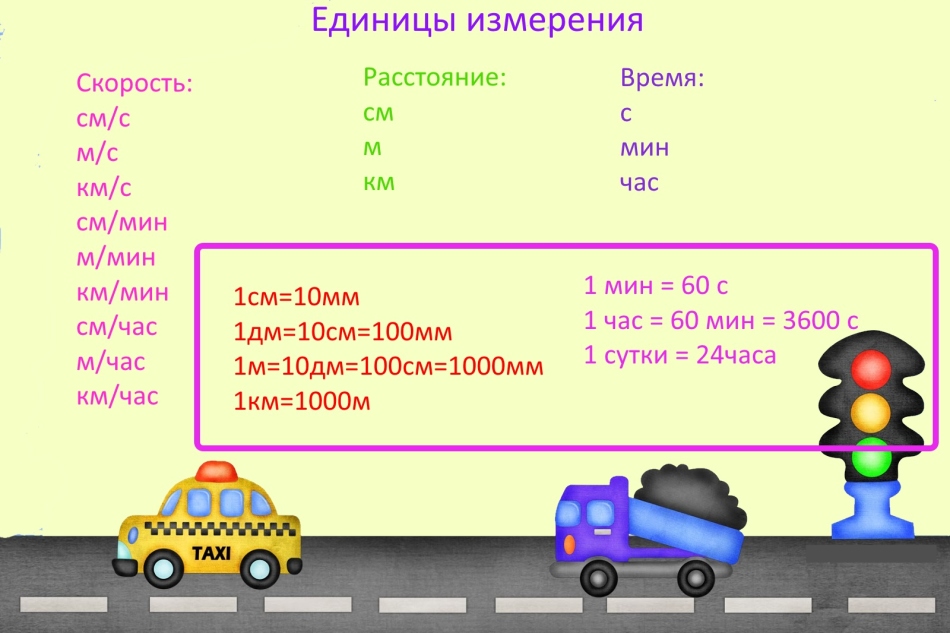
Enote
Ko rešijo težave glede hitrosti, časa in razdalje, se pogosto zmotijo, ker so pozabili prevesti merske enote.
Pomembno: Enote merjenja so lahko kakršne koli, če pa obstajajo različne enote meritev v eni nalogi, jih prevedite enako. Na primer, če se hitrost meri v kilometrih na minuto, je treba razdaljo predstaviti v kilometrih in čas v nekaj minutah.
Za radovedno: Splošno sprejet sistem ukrepov se zdaj imenuje Metric, vendar to ni bilo vedno tako, v starih časih pa so bile uporabljene druge enote dimenzije Rus.

Naloga boas: Slon in opica sta s koraki izmerila dolžino konstriktorja boa. Pomikali so se drug proti drugemu. Hitrost opice je bila v eni sekundi 60 cm, hitrost slona pa 20 cm v eni sekundi. Za merjenje so porabili 5 sekund. Kakšna je dolžina konstriktorja boa? (odločitev pod sliko)

Odločitev:
Iz pogojev problema ugotovimo, da poznamo hitrost opice in slona ter čas, ki ga potrebujejo za merjenje dolžine povečanja.
Zapišemo te podatke:
Opica hitrost - 60 cm/s
Hitrost slona - 20 cm/s
Čas - 5 sekund
Razdalja ni znana
Te podatke pišemo z matematičnimi znaki:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 sekund
S -?
Napišite formulo za razdaljo, če sta znana hitrost in čas:
S \u003d v ⋅ t
Izračunamo, kako je razdalja opica pretekel:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Zdaj pa izračunajmo, koliko je prešel slon:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Povzemamo razdaljo, ki jo je opica in razdalja, ki jo je pretekel slon:
S \u003d s1 + s2 \u003d 300 + 100 \u003d 400 cm
Graf hitrosti telesa na čas: fotografija
Razdalja premaga z različnimi hitrostmi v različnih časih. Večja kot je hitrost, manj časa bo trajalo.
Tabela 4 Razred: hitrost, čas, razdalja
Spodnja tabela prikazuje podatke, za katere morate najti težave, in jih nato rešiti.
| № | Hitrost (km/uro) | Čas (ura) | Razdalja (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Lahko si fantazirate in sami izmislite naloge za mizo. Spodaj so naše možnosti za naloge:
- Mama je babici poslala rdeč klobuk. Deklica se je nenehno motila in počasi hodila po gozdu, s hitrostjo 5 km/h. 2 uri je preživela na poti. Kakšna razdalja je v tem času minil rdeča kapica?
- Poštar Pechkin vzame paket na kolesu s hitrostjo 12 km/h. Ve, da je razdalja med njegovo hišo in hišo strica Fedorja 12 km. Pomagajte Pechkin Izračunajte, koliko časa bo trajalo za cesto?
- Oče Ksyusha je kupil avto in se odločil, da bo svojo družino odpeljal v morje. Avto je vozil s hitrostjo 60 km/h, na cesti pa so preživeli 4 ure. Kakšna je razdalja med hišo Ksyusha in morsko obalo?
- Race so se zbrale v klinu in priletele v tople robove. Ptice so mahale s krili utrujene 3 ure in v tem času premagale 300 km. Kakšna je bila hitrost ptic?
- Letalo AN-2 leti s hitrostjo 220 km/h. Odletel je iz Moskve in odletel v Nizhny Novgorod, razdalja med tema dvema mestma je 440 km. Kako dolgo bo šlo letalo?

Odgovore na zgornje naloge najdete v spodnji tabeli:
| № | Hitrost (km/uro) | Čas (ura) | Razdalja (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Primeri reševanja težav za hitrost, čas, razdaljo za 4. razred
Če je v eni nalogi več predmetov gibanja, morate otroka naučiti, da gibanje teh predmetov obravnava ločeno in šele nato skupaj. Primer takšne naloge:
Dva prijatelja Vadika in tema sta se odločila, da se sprehodita in pustila svoje hiše drug proti drugemu. Vadik je vozil s kolesom in tema je hodila. Vadik je vozil s hitrostjo 10 km/h, tema pa je bila s hitrostjo 5 km na uro. Uro kasneje sta se srečala. Kakšna je razdalja med Vadikovimi hišami in temami?
To težavo je mogoče rešiti s formulo za odvisnost razdalje od hitrosti in časa.
S \u003d v ⋅ t
Razdalja, ki jo je Vadik vozil na kolesu, bo enaka njegovi hitrosti, pomnožena s potovanjem.
S \u003d 10 ⋅ 1 \u003d 10 kilometrov
Razdalja, ki jo je prenesla tema, velja podobno:
S \u003d v ⋅ t
Digitalne vrednosti njene hitrosti in časa nadomestimo v formulo
S \u003d 5 ⋅ 1 \u003d 5 kilometrov
Razdaljo, ki jo je vozil Vadik, je treba dodati na razdaljo, ki jo je tema prenesla.
10 + 5 \u003d 15 kilometrov
Kako se naučiti, kako rešiti zapletene težave, za reševanje, na katere morate razmišljati logično?
Če želite razviti logično razmišljanje otroka, morate z njim rešiti preproste in nato zapletene logične težave. Te naloge so lahko sestavljene iz več stopenj. Iz ene faze v drugo je mogoče premakniti le, če je prejšnja rešena. Primer takšne naloge:
Anton se je s kolesom odpravil s hitrostjo 12 km/h, Lisa pa se je s hitrostjo 2 -krat manjšala po skuterju kot Anton, Denis pa je hodil s hitrostjo 2 -krat manj kot hitrost Lise. Kakšna je Denisova hitrost?
Če želite rešiti to težavo, morate najprej ugotoviti hitrost Lise in šele po tej hitrosti Denisa.

Včasih v učbenikih za 4 ocene obstajajo težke naloge. Primer takšne naloge:
Dva kolesarja sta pustila drugačna mesta drug proti drugemu. Eden od njih je pohitel in dirkal s hitrostjo 12 km/h, drugi pa se je počasi vozil s hitrostjo 8 km/h. Razdalja med mesti, iz katerih so kolesarji pustili 60 km. Kakšna razdalja bo prehodila vsak kolesar, preden se bosta srečala? (odločitev pod fotografijo)

Odločitev:
- 12+8 \u003d 20 (km/h) je skupna hitrost dveh kolesarjev ali hitrost, s katero sta se približala drug drugemu
- 60 : 20 \u003d 3 (ure) - to je čas, skozi katerega so se srečali kolesarji
- 3 ⋅ 8 \u003d 24 (km) je razdalja, ki jo je vozil prvi kolesar
- 12 ⋅ 3\u003d 36 (km) je razdalja, ki jo je vozil drugi kolesar
- Preverjanje: 36+24 \u003d 60 (km) je razdalja, ki sta jo prehodila dva kolesarja.
- Odgovor: 24 km, 36 km.
Ponudite otroke v obliki igre za reševanje takšnih težav. Morda bodo sami želeli sestaviti svojo nalogo o prijateljih, živalih ali pticah.







