Vzorec objemu a plochy celého povrchu gule, guľôčkovou guľou a priemerom gule: hodnota. Príklady výpočtu povrchovej plochy a objemu gule cez polomer a priemer lopty: popis. Ako nájsť objem lopty cez povrchovú plochu gule: príklad

Článok bude užitočný pre školákov a budúcich žiadateľov, ktorí sa pripravujú na skúšku.

Vzorec objemu lopty cez polomer: Význam

Objem gule V sa vypočíta vzorcom (pozri nižšie), kde r je polomer lopty, číslo „pi“ - π je matematická konštanta, ≈ 3,14.

Tento vzorec je základňou!

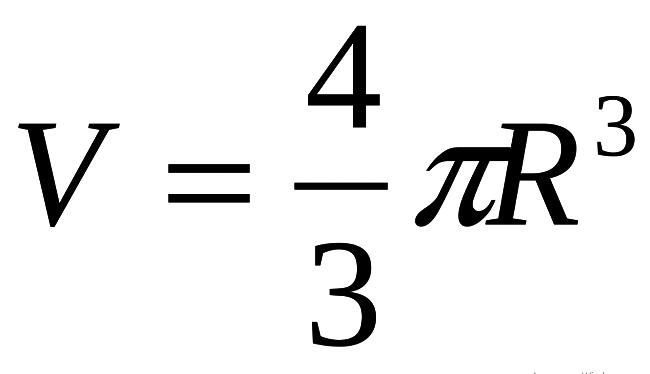
Vzorec objemu gule cez priemer: hodnota

1. Použite základný vzorec: v \u003d 4/3*π*r³.
2. Polomer R je priemer ½ D alebo r \u003d d/2.
3. Preto: v \u003d 4/3*π*r³ → V \u003d (4π/3)*(d/2) ³ → V \u003d (4π/3)*(dft/8) → V \u003d πD.³/6.

Alebo

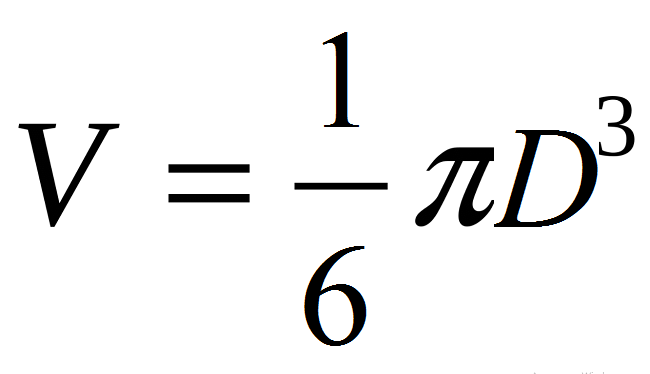
Príklady výpočtu objemu gule cez polomer a priemer lopty: Opis

Úloha 1.

Polomer lopty je 10 cm. Nájdite jeho objem.

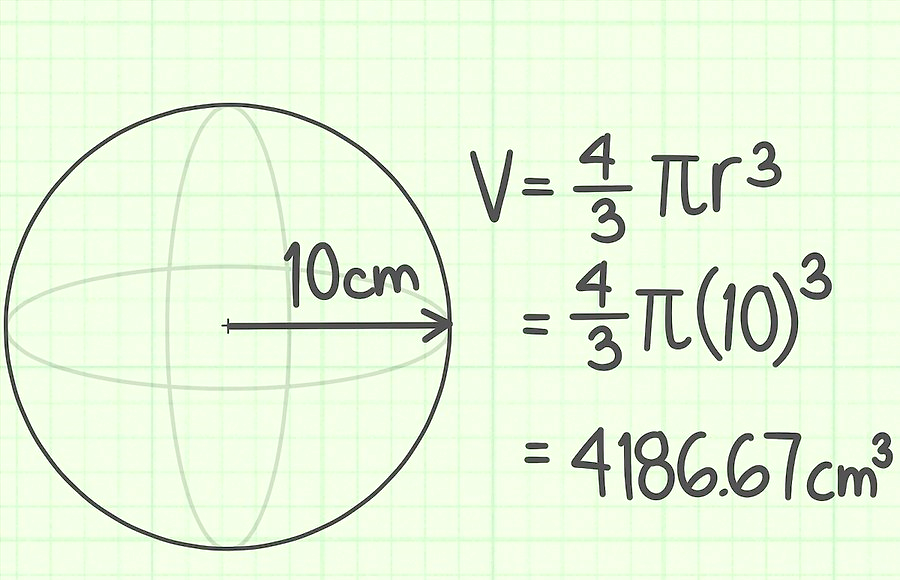
Úloha 2.

Priemer gule je 10 cm. Nájdite jeho objem.

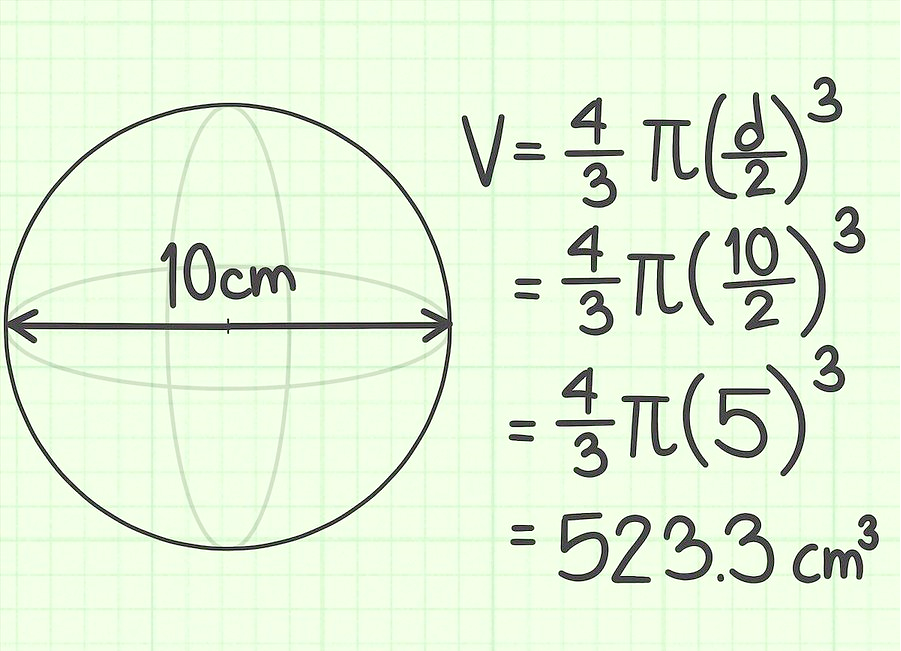
Úloha 3.

Pomer priemeru mesiaca a priemer Zeme 1: 4. Koľkokrát je objem Zeme väčší ako objem mesiaca?

Riešenie:

Odpoveď: 64 krát.

Dôležitý: Existuje veľa online kalkulačiek, ktoré vám umožňujú rýchlo nájsť danú hodnotu. Napríklad služba Webmath.

Vzorec celej povrchu gule, guľa cez polomer: Význam

Povrchová plocha gule/gule sa vypočíta podľa vzorca (pozri nižšie), kde r je polomer lopty, číslo „pi“ - π je matematická konštanta, ≈ 3,14.

Tento vzorec je základňou!

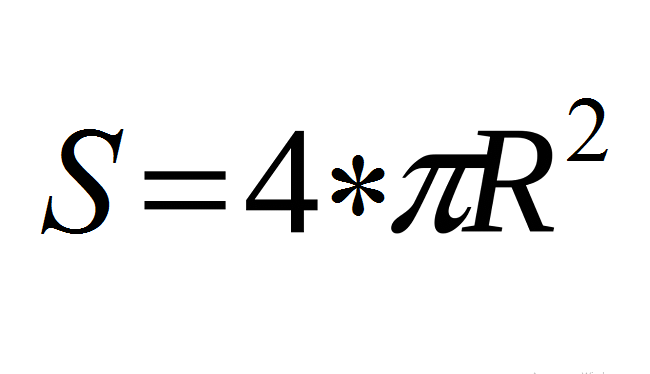
Vzorec úplného povrchu gule, guľa cez priemer: hodnota

1. Použite základný vzorec: S \u003d 4*π*R².
2. Polomer R je priemer ½ D alebo r \u003d d/2.
3. Odtiaľ: S \u003d 4*π*R² → S \u003d 4*π*(D/2) ² → S \u003d (4π)*(D²/4) → S \u003d (4πd²)/4 → S \u003d πD.².

Alebo

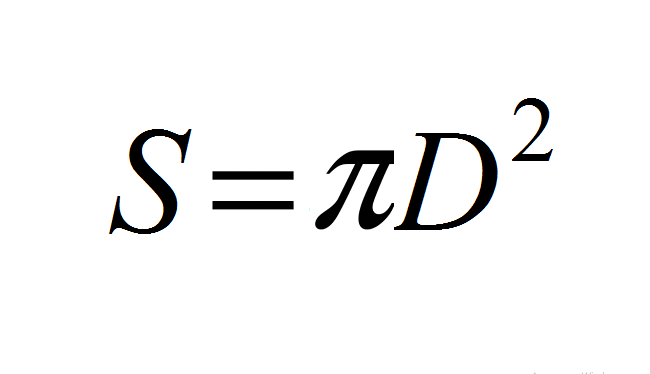
Príklady výpočtu povrchovej plochy, gule gule, cez polomer a priemer lopty: Opis

Úloha 4.

Úloha 5.

Úloha 6.

Ako nájsť objem lopty cez povrchovú plochu gule, guľa: príklad riešenia problému

Úloha 7.

Úloha 8.

Video: Používajte matematiku. Objem a plocha povrchu telies rotácie.