Como encontrar uma área quadrada se o perímetro for conhecido, diagonal? Como encontrar o quadrado do quadrado inscrito no círculo e descrito próximo à circunferência: fórmula, exemplos de problemas de resolução. Como encontrar o lado e a diagonal da praça, se sua área for conhecida?

Leia o artigo para saber como encontrar a área quadrada de maneiras diferentes.

Um quadrado é um retângulo equilátero. Este quadrilátero adequado e plano tem igualdade em todos os lados, cantos e diagonais. Devido ao fato de que existe tanta igualdade, a fórmula para calcular a área e outras características é ligeiramente modificada em comparação com outras figuras matemáticas. Mas isso não torna as tarefas muito complicadas. Vamos analisar todas as fórmulas e soluções para este artigo.

Como encontrar o lado da praça, conhecendo sua área?

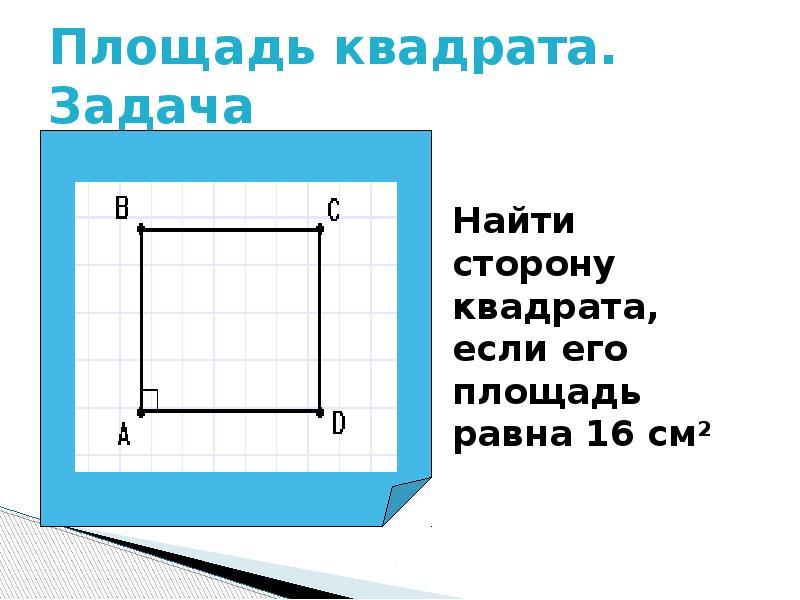
Quadrado S. Os quadrados diretos e quadrados são calculados pela fórmula: uma Multiplique por b.. Mas como o quadrado tem uma igualdade completa das partes, sua área será igual: S \u003d (a) no segundo grau.  Como descobrir o tamanho do lado da praça, conhecendo sua área?

• Se a área do quadrado é conhecido, encontraremos o lado calculando a área sob a raiz quadrada.
• Por exemplo, a área do quadrado é de 49, então a que o lado é igual?
• 49 \u003d (a) no segundo grau. Solução: a \u003d raiz de 49 \u003d 7. Resposta: 7.

Se você precisar encontrar o lado do quadrado, cuja área é muito longa, use a calculadora. Primeiro disque o número da área e pressione o sinal raiz no teclado da calculadora. O número resultante será a resposta.

Como encontrar uma diagonal quadrada se sua área for conhecida?

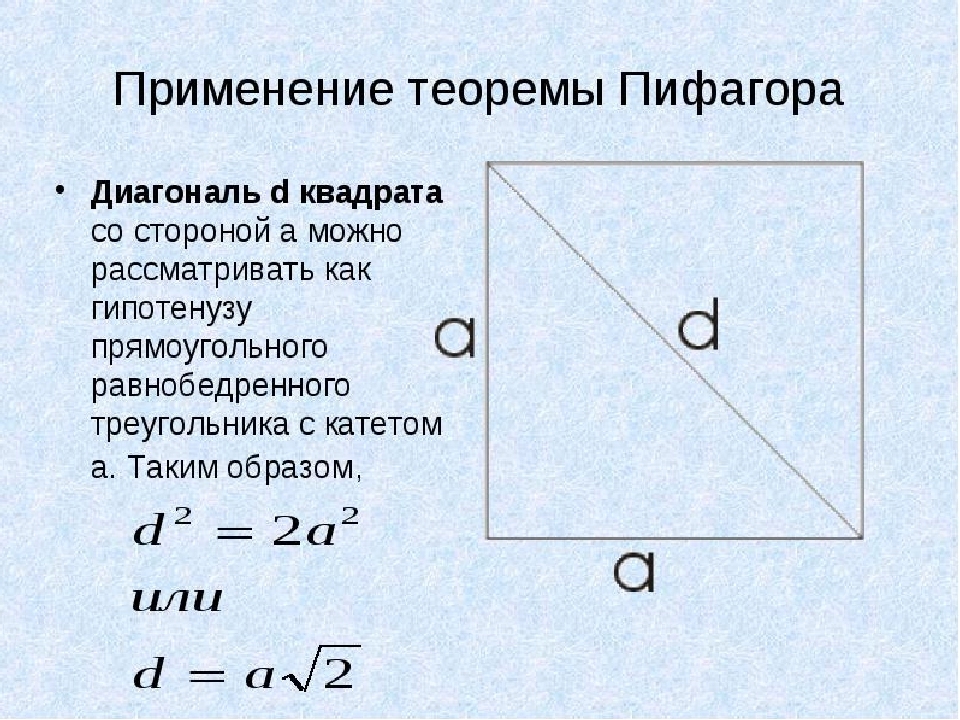
Neste exemplo, usaremos o teorema de Pitágoras. Em um quadrado, todos os lados são iguais e a diagonal d. Consideraremos como hipotenusa de um triângulo retangular de isósceles com uma perna uma. Agora encontramos uma diagonal quadrada se sua área for conhecida:

• Para não pintar todo o teorema de Pitágoras, decidiremos sobre a segunda opção: d \u003d Aising, onde A é o lado do quadrado.
• Então, sabemos a área da praça, por exemplo, é igual a 64. Então, um lado a \u003d √64 \u003d 8.
• Acontece que D \u003d 8√2. A raiz de 2 não produz todo o número; portanto, na resposta, você pode escrever da seguinte maneira: d \u003d 8√2. Mas, se você deseja calcular o valor, use a calculadora: √2 \u003d 1.41421356237 e multiplicar por 8, acontece 11, 3137084.

Importante: Normalmente, em matemática, nenhum número com um grande número de números é deixado em resposta. É necessário arredondar ou sair com a raiz. Portanto, a resposta para a diagonal é se a área for 64 da seguinte forma: d \u003d 8√2.

Como encontrar uma área quadrada através de uma diagonal?

A fórmula para encontrar a área quadrada através da diagonal é simples:

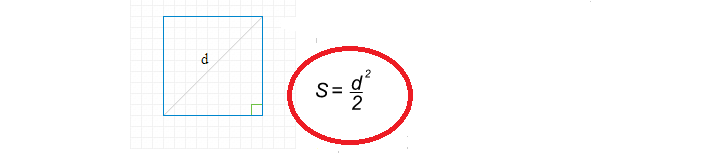
Agora vamos escrever uma solução para encontrar a área quadrada através da diagonal:

• Diagonal d \u003d 8.
• 8 no quadrado é 64.
• 64 Divida por 2 Igual 32.
• A área quadrada é de 32.

Adendo: Esta tarefa tem outra solução através do teorema de Pitágoras, mas é mais complexa. Portanto, use a solução que examinamos.

Como encontrar uma área quadrada, conhecendo seu perímetro?

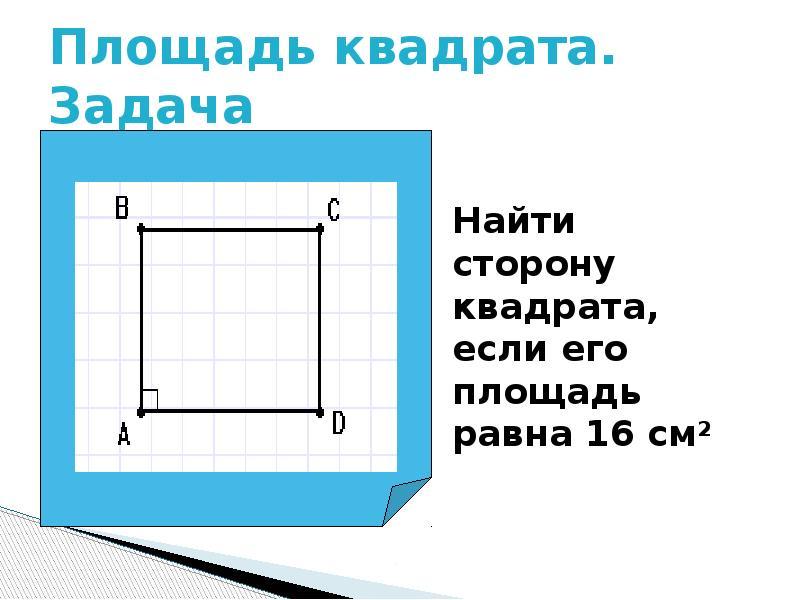
O perímetro do quadrado quadrado P. - Esta é a soma de todas as partes. Para encontrar sua área, conhecendo seu perímetro, você deve primeiro calcular o lado do quadrado quadrado. Solução:

• Suponha que o perímetro seja 24. Divida 24 em 4 lados, acontece 6 - este é um lado.
• Agora usamos a fórmula para encontrar a área, sabendo qual é o lado do quadrado quadrado: S \u003d a em um quadrado, s \u003d 6 em um quadrado \u003d 36.
• Responda: 36

Como você pode ver, conhecendo o perímetro da praça, basta encontrar sua área.

Como encontrar uma área de um quadrado inscrito em um círculo com um determinado raio?

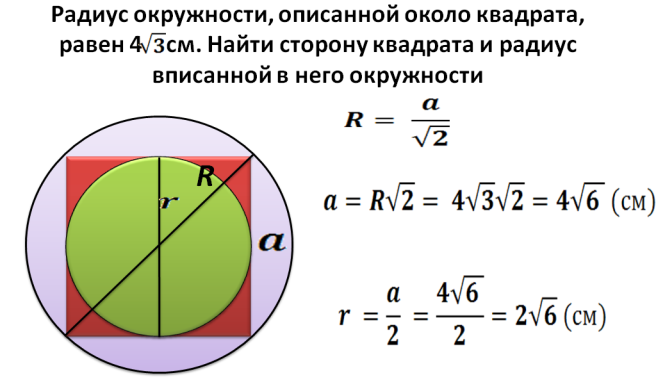
Raio R - Esta é metade da diagonal de um quadrado inscrito em círculo. Agora podemos encontrar uma diagonal pela fórmula: d \u003d 2*r. Em seguida, encontramos o quadrado do quadrado inscrito em um círculo com um determinado raio:

• A diagonal é 2 multiplique pelo raio. Por exemplo, o raio é 5, então a diagonal é igual 2*5=10.
• Foi descrito acima como encontrar o quadrado do quadrado se a diagonal for conhecida: S \u003d diagonal em um quadrado dividido em 2. s \u003d 10*10 e divida por 2 \u003d 50.
• Responda - 50.

Essa tarefa é um pouco mais complicada, mas também é facilmente resolvida se você conhece todas as fórmulas.

Como encontrar uma área de um quadrado descrito perto de um círculo com um determinado raio?

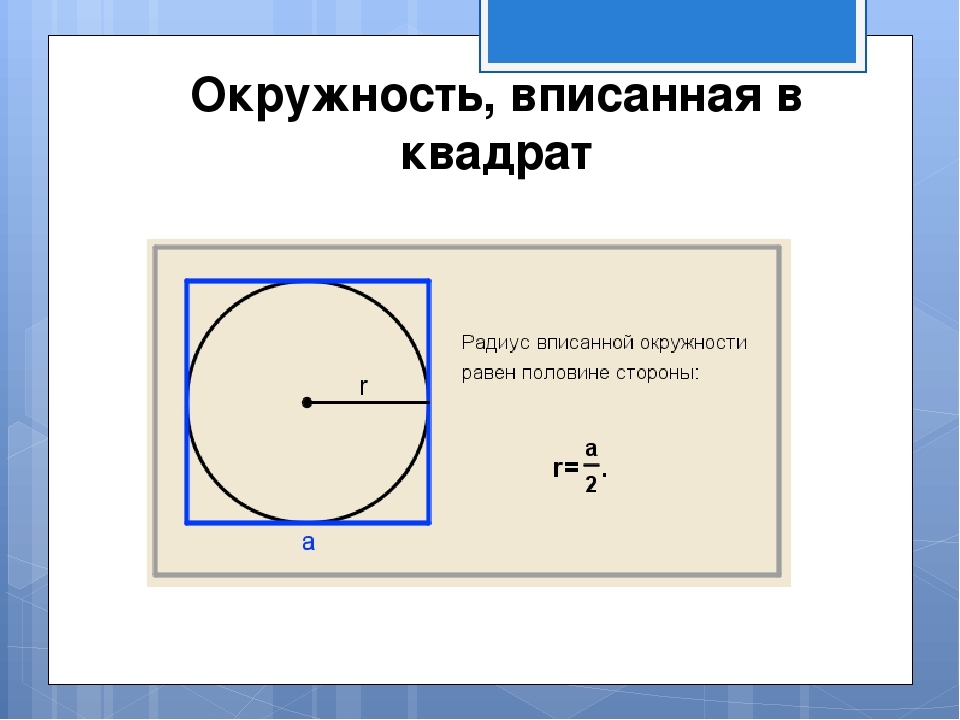
A figura mostra que o raio do círculo inscrito é igual a metade do lado. O lado está localizado de acordo com a fórmula reversa que descreveu na figura: a \u003d 2*r. Então encontramos a área do quadrado descrito perto do círculo com um determinado raio de acordo com a fórmula S \u003d e em um quadrado. Solução:

• Suponha que o raio seja 7. O lado do quadrado A é 2*7 \u003d 14.
• S \u003d 14 em um quadrado \u003d 196.

Se você entender a essência de resolver esses problemas, poderá resolvê -los de maneira rápida e simples. Vejamos mais alguns exemplos.

Exemplos de resolução de problemas no tópico "quadrado"

Para corrigir o material coberto e lembrar de todas as fórmulas, é necessário resolver vários exemplos de problemas com o tema da "área quadrada". Começamos com uma tarefa simples e passamos a resolver mais complexos:

Agora você sabe como usar a fórmula para o quadrado do quadrado, o que significa que você pode executar qualquer tarefa. Sucesso no treinamento futuro!

VÍDEO: Cálculo da área quadrada