Como resolver movimentos para movimento? A fórmula de dependência entre velocidade, tempo e distância. Tarefas e soluções.
Contente
- A fórmula para a dependência de tempo, velocidade e distância na 4ª série: como é velocidade, tempo, distância?
- Como encontrar tempo, conhecimento de velocidade e distância?
- Como encontrar velocidade se o tempo e a distância forem conhecidos?
- Como encontrar uma distância se o tempo e a velocidade forem conhecidos?
- Gráfico da velocidade corporal no tempo: foto
- Tabela 4 Classe: velocidade, tempo, distância
- Exemplos de problemas de resolução para velocidade, tempo, distância para a 4ª série
- Vídeo: tarefas de movimento
A fórmula para a dependência de tempo, velocidade e distância na 4ª série: como é velocidade, tempo, distância?
Pessoas, animais ou carros podem se mover a uma certa velocidade. Por um certo tempo, eles podem seguir um certo caminho. Por exemplo: hoje você pode chegar à sua escola em meia hora. Você vai a uma certa velocidade e supera 1000 metros em 30 minutos. O caminho que é superado é designado em matemática pela carta S.. A velocidade é indicada pela letra v. E o tempo pelo qual o caminho foi negado é indicado pela letra t.
- Caminho - S.
- Velocidade- v
- Tempo - t
Se você estiver atrasado para a escola, pode seguir o mesmo caminho em 20 minutos, aumentando sua velocidade. Portanto, o mesmo caminho pode ser percorrido em momentos diferentes e em velocidades diferentes.
Como o tempo de passagem depende da velocidade?
Quanto maior a velocidade, mais rápida será a distância. E quanto menor a velocidade, mais tempo você precisa passar no caminho.

Como encontrar tempo, conhecimento de velocidade e distância?
Para encontrar o tempo que você precisa passar no caminho, você precisa saber a distância e a velocidade. Se a distância for dividida em velocidade, você descobrirá o tempo. Um exemplo dessa tarefa:
A tarefa da lebre. A lebre fugiu do lobo a uma velocidade de 1 quilômetro por minuto. Ele correu para o seu buraco a 3 quilômetros. Para que horas a lebre alcançou um buraco?

Como é fácil resolver os problemas de movimento, onde você precisa encontrar uma distância, tempo ou velocidade?
- Leia cuidadosamente a tarefa e determine o que se sabe a partir das condições do problema.
- Escreva esses dados no rascunho.
- Escreva também o que é desconhecido e o que precisa ser encontrado
- Use a fórmula para tarefas sobre distância, tempo e velocidade
- Insira os dados conhecidos na fórmula e resolva o problema
Solução para o problema sobre a lebre e o lobo.
- A partir das condições do problema, determinamos que conhecemos velocidade e distância.
- Além disso, pelas condições do problema, determinamos que precisamos encontrar o tempo que a lebre precisava para alcançar o buraco.

Escrevemos para o rascunho desses dados, por exemplo:
Distância a buraco - 3 quilômetros
Velocidade da lebre - 1 quilômetro em 1 minuto
O tempo é desconhecido
Agora escrevemos o mesmo que sinais matemáticos:
S. - 3 quilômetros
V - 1 km/min
t — ?
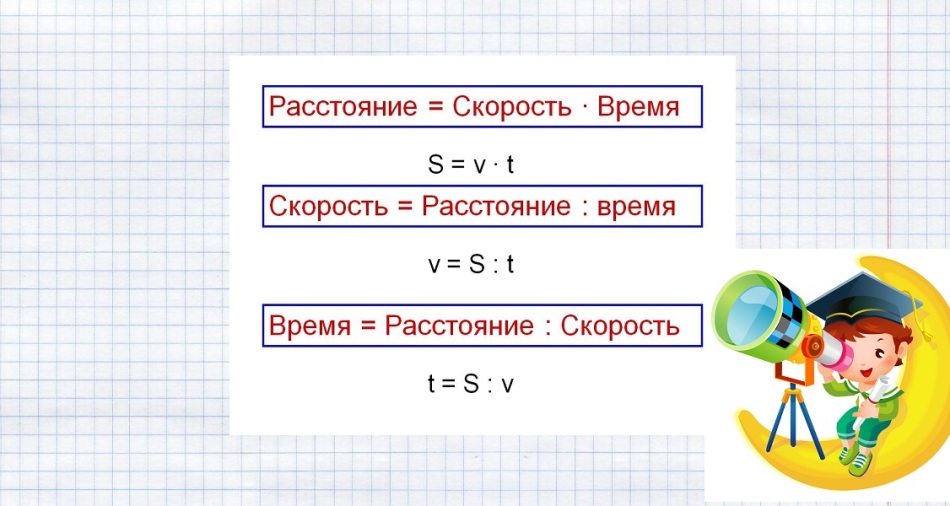
Recordamos e escrevemos uma fórmula para encontrar o tempo no caderno:
t \u003d s: v
Agora escrevemos a solução do problema com os números:
t \u003d 3: 1 \u003d 3 minutos
Como encontrar velocidade se o tempo e a distância forem conhecidos?
Para encontrar velocidade, se o tempo e a distância forem conhecidos, a distância deve ser dividida por um tempo. Um exemplo dessa tarefa:
A lebre fugiu do lobo e correu para o seu buraco a 3 quilômetros. Ele superou essa distância em 3 minutos. Em que velocidade a lebre correu?
Resolvendo o problema do movimento:
- No rascunho, escrevemos que conhecemos a distância e o tempo.
- A partir das condições do problema, determinamos o que precisa ser encontrado velocidade
- Lembre -se da fórmula para encontrar velocidade.
As fórmulas para resolver esses problemas são mostradas na figura abaixo.
Substituímos os dados conhecidos e resolvemos o problema:
Distância a buraco - 3 quilômetros
O tempo para o qual a lebre atingiu o buraco é de 3 minutos
A velocidade é desconhecida
Escrevemos esses dados conhecidos com sinais matemáticos
S. - 3 quilômetros
t - 3 minutos
v -?
Registre a fórmula para encontrar velocidade
v \u003d s: t
Agora escrevemos a solução do problema com os números:
v \u003d 3: 3 \u003d 1 km/min

Como encontrar uma distância se o tempo e a velocidade forem conhecidos?
Para encontrar uma distância, se for tempo e velocidade conhecidos, é necessário se multiplicar por velocidade. Um exemplo dessa tarefa:
A lebre fugiu do lobo a uma velocidade de 1 quilômetro em 1 minuto. Levou três minutos para correr para o buraco. Que distância a lebre correu?
Solução do problema: Escrevemos para um rascunho que conhecemos pelas condições do problema:
Velocidade da lebre - 1 quilômetro em 1 minuto
O tempo em que a lebre fugiu para Nora é de 3 minutos
A distância é desconhecida
Agora, escreveremos a mesma coisa com sinais matemáticos:
v - 1 km/min
t - 3 minutos
S -?
Lembre -se da fórmula para encontrar a distância:
S \u003d v ⋅ t
Agora escrevemos a solução do problema com os números:
S \u003d 3 ⋅ 1 \u003d 3 km

Como aprender a resolver problemas mais complexos?
Para aprender a resolver tarefas mais complexas, você precisa entender como as tarefas simples são resolvidas, lembre -se de quais sinais indicam a distância, velocidade e tempo. Se não for possível lembrar as fórmulas matemáticas, elas precisam ser escritas em uma folha de papel e sempre manter à mão enquanto resolvendo problemas. Resolva com seu filho tarefas simples que podem ser inventadas em movimento, por exemplo, durante uma caminhada.

Unidades
Quando resolvem problemas sobre velocidade, tempo e distância, geralmente cometem um erro, devido ao fato de esquecerem traduzir unidades de medição.
IMPORTANTE: As unidades de medição podem ser qualquer, mas se houver diferentes unidades de medições em uma tarefa, traduzi -las da mesma forma. Por exemplo, se a velocidade for medida em quilômetros por minuto, a distância deverá ser apresentada em quilômetros e tempo em minutos.
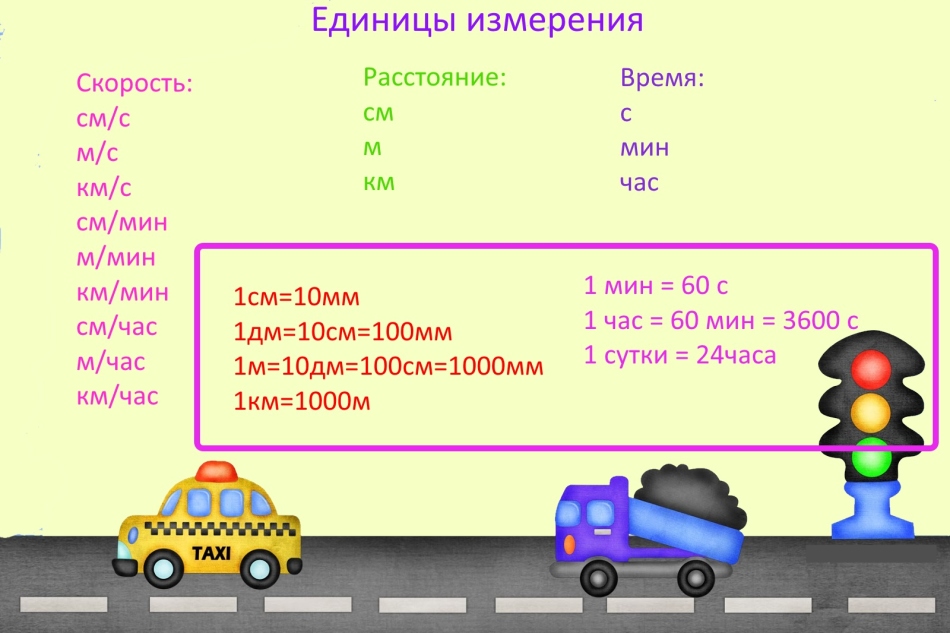
Para curioso: O sistema geralmente aceito de medidas é chamado de métrica agora, mas esse nem sempre era o caso e, nos velhos tempos na Rússia, outras unidades de dimensão eram usadas.

A tarefa dos boas: O elefante e o macaco mediram o comprimento do construtor da BoA com etapas. Eles se mudaram um para o outro. A velocidade do macaco foi de 60 cm em um segundo, e a velocidade do elefante é de 20 cm em um segundo. Eles passaram 5 segundos na medição. Qual é o comprimento do construtor da BoA? (Decisão sob a foto)

Solução:
A partir das condições do problema, determinamos que conhecemos a velocidade do macaco e do elefante e o tempo que eles precisavam para medir o comprimento do impulso.
Nós escrevemos estes dados:
Velocidade de macaco - 60 cm/s
Velocidade de elefante - 20 cm/s
Tempo - 5 segundos
A distância é desconhecida
Escrevemos esses dados com sinais matemáticos:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 segundos
S -?
Vamos escrever a fórmula para a distância se a velocidade e o tempo forem conhecidos:
S \u003d v ⋅ t
Calculamos a distância que o macaco passou:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Agora vamos calcular o quanto o elefante passou:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Resumimos a distância que o macaco e a distância que o elefante passou:
S \u003d s1 + s2 \u003d 300 + 100 \u003d 400 cm
Gráfico da velocidade corporal no tempo: foto
A distância superada com velocidades diferentes é superada em diferentes tempos. Quanto maior a velocidade, menos tempo levará.
Tabela 4 Classe: velocidade, tempo, distância
A tabela abaixo mostra os dados para os quais você precisa ter problemas e resolvê -los.
| № | Velocidade (km/hora) | Hora (hora) | Distância (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Você pode fantasiar e criar tarefas para a mesa. Abaixo estão nossas opções para tarefas:
- Mamãe enviou um chapéu vermelho para a avó. A garota estava constantemente distraída e caminhava pela floresta lentamente, a uma velocidade de 5 km/h. Ela passou 2 horas no caminho. Que distância passou uma tampa vermelha durante esse período?
- O Postman Pechkin pega um pacote em uma bicicleta a uma velocidade de 12 km/h. Ele sabe que a distância entre sua casa e a casa do tio Fedor fica a 12 km. Ajude Pechkin a calcular quanto tempo levará para a estrada?
- Papai Ksyusha comprou um carro e decidiu levar sua família ao mar. O carro estava dirigindo a uma velocidade de 60 km/h e 4 horas foram gastas na estrada. Qual é a distância entre a casa de Ksyusha e a costa do mar?
- Os patos se reuniram na cunha e voaram para as bordas quentes. Os pássaros acenaram com as asas cansadas por 3 horas e venceram 300 km durante esse período. Qual era a velocidade dos pássaros?
- A aeronave AN-2 voa a uma velocidade de 220 km/h. Ele saiu de Moscou e voa para Nizhny Novgorod, a distância entre essas duas cidades é de 440 km. Quanto tempo o avião vai durar?

As respostas para as tarefas acima podem ser encontradas na tabela abaixo:
| № | Velocidade (km/hora) | Hora (hora) | Distância (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Exemplos de problemas de resolução para velocidade, tempo, distância para a 4ª série
Se houver vários objetos de movimento em uma tarefa, você precisará ensinar à criança a considerar o movimento desses objetos separadamente e somente juntos. Um exemplo dessa tarefa:
Dois amigos de Vadik e o tópico decidiram dar um passeio e deixaram suas casas um para o outro. Vadik montou uma bicicleta, e o tópico estava andando. Vadik montou a uma velocidade de 10 km/h, e o tópico estava a uma velocidade de 5 km por hora. Uma hora depois, eles se conheceram. Qual é a distância entre as casas e tópicos de Vadik?
Esse problema pode ser resolvido usando a fórmula para a dependência da distância na velocidade e no tempo.
S \u003d v ⋅ t
A distância que Vadik dirigiu em uma bicicleta será igual à sua velocidade multiplicada por viagens.
S \u003d 10 ⋅ 1 \u003d 10 quilômetros
A distância que o tópico passou é considerada da mesma forma:
S \u003d v ⋅ t
Substituímos os valores digitais de sua velocidade e tempo na fórmula
S \u003d 5 ⋅ 1 \u003d 5 quilômetros
A distância que Vadik dirigiu deve ser adicionada à distância que o tópico passou.
10 + 5 \u003d 15 quilômetros
Como aprender a resolver problemas complexos, para resolver o que você precisa pensar logicamente?
Para desenvolver o pensamento lógico da criança, você precisa resolver com ele problemas lógicos simples e depois complexos. Essas tarefas podem consistir em vários estágios. Só é possível passar de um estágio para outro se o anterior for resolvido. Um exemplo dessa tarefa:
Anton entrou em uma bicicleta a uma velocidade de 12 km/h, e Lisa andou em uma scooter a uma velocidade 2 vezes menor que a de Anton, e Denis caminhou a uma velocidade 2 vezes menor que a de Lisa. Qual é a velocidade de Denis?
Para resolver esse problema, você deve primeiro descobrir a velocidade de Lisa e somente depois da velocidade de Denis.

Às vezes, nos livros didáticos para 4 séries, existem tarefas difíceis. Um exemplo dessa tarefa:
Dois ciclistas deixaram diferentes cidades um para o outro. Um deles se apressou e correu a uma velocidade de 12 km/h, e o segundo correu lentamente a uma velocidade de 8 km/h. A distância entre as cidades das quais os ciclistas deixaram 60 km. Que distância cada ciclista passará, antes de se encontrar? (decisão sob a foto)

Solução:
- 12+8 \u003d 20 (km/h) é a velocidade total de dois ciclistas, ou a velocidade com que se aproximaram
- 60 : 20 \u003d 3 (horas) - Este é o momento em que os ciclistas se conheceram
- 3 ⋅ 8 \u003d 24 (km) é a distância que o primeiro ciclista dirigiu
- 12 ⋅ 3\u003d 36 (km) é a distância que o segundo ciclista dirigiu
- Verificação: 36+24 \u003d 60 (km) é a distância que dois ciclistas percorreram.
- Resposta: 24 km, 36 km.
Ofereça às crianças na forma de um jogo para resolver esses problemas. Talvez eles mesmos desejem compor sua tarefa sobre amigos, animais ou pássaros.







