O artigo será útil para crianças em idade escolar e futuros candidatos que estão se preparando para o exame.
Contente
- Fórmula do volume da bola através do raio: significado
- Fórmula do volume da bola através do diâmetro: valor
- Exemplos de cálculo do volume da bola, através do raio e do diâmetro da bola: Descrição
- Fórmula da superfície completa da bola, esfera através do raio: significado
- A fórmula da superfície completa da bola, esfera através do diâmetro: valor
- Exemplos de cálculo da área da superfície, esfera da bola, através do raio e diâmetro da bola: Descrição
- Como encontrar o volume da bola na área da superfície da bola, esfera: um exemplo de resolução de um problema
- VÍDEO: Use matemática. O volume e a área da superfície dos corpos de rotação.
Fórmula do volume da bola através do raio: significado
O volume da bola V é calculado pela fórmula (veja abaixo), onde R é o raio da bola, o número “Pi” - π é uma constante matemática, ≈ 3,14.
Esta fórmula é a base!
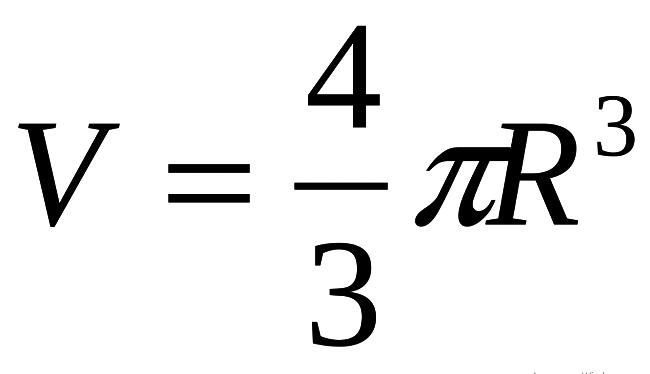
Fórmula do volume da bola através do diâmetro: valor
- Use a fórmula base: v \u003d 4/3*π*r³.
- O raio r é ½ diâmetro d ou r \u003d d/2.
- Portanto: v \u003d 4/3*π*r³ → v \u003d (4π/3)*(d/2) ³ → v \u003d (4π/3)*(d³/8) → V \u003d πD.³/6.
Ou
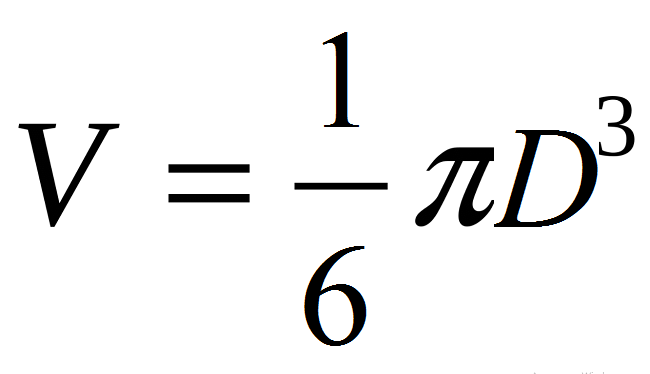
Exemplos de cálculo do volume da bola, através do raio e do diâmetro da bola: Descrição
Tarefa 1.
O raio da bola é de 10 cm. Encontre seu volume.
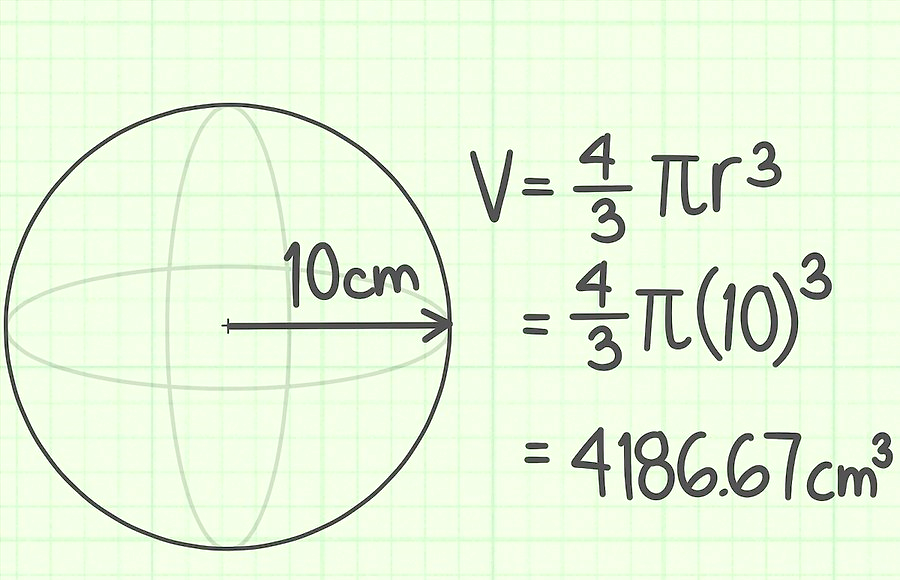
Tarefa 2.
O diâmetro da bola é de 10 cm. Encontre seu volume.
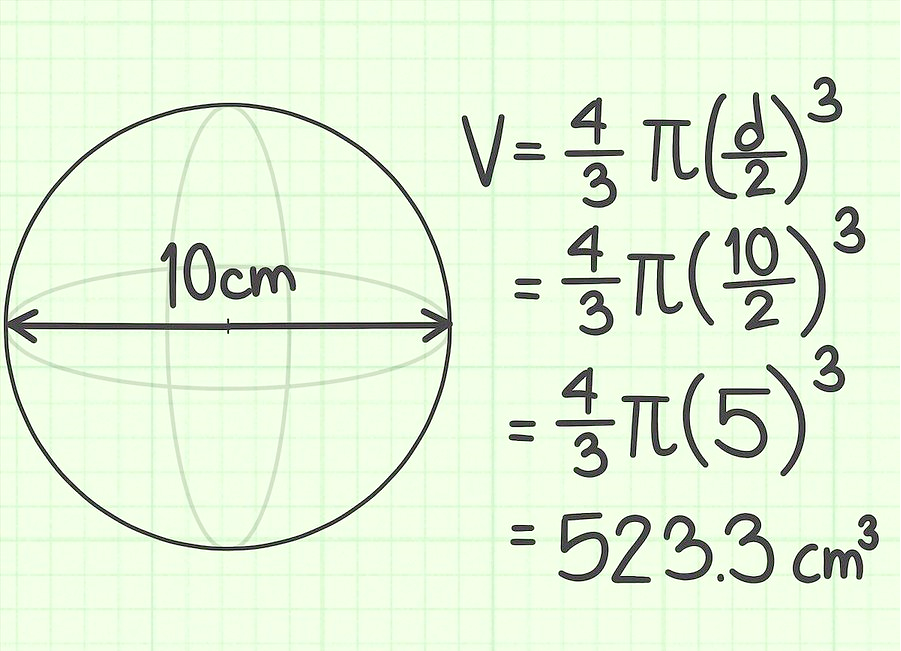
Tarefa 3.
A proporção do diâmetro da lua e o diâmetro da Terra 1: 4. Quantas vezes o volume da terra é maior que o volume da lua?
Solução:
Resposta: 64 vezes.
Importante: Existem muitas calculadoras on -line que permitem que você encontre rapidamente um determinado valor. Por exemplo, serviço Webmath.
Fórmula da superfície completa da bola, esfera através do raio: significado
A área de superfície da esfera/bola é calculada de acordo com a fórmula (veja abaixo), onde r é o raio da bola, o número "pi" - π é uma constante matemática, ≈ 3,14.
Esta fórmula é a base!
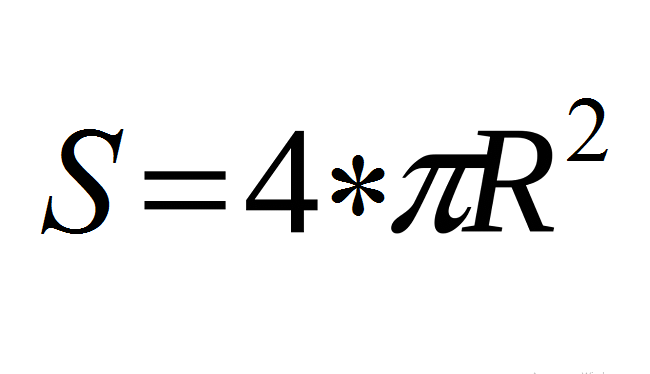
A fórmula da superfície completa da bola, esfera através do diâmetro: valor
- Use a fórmula base: s \u003d 4*π*r².
- O raio r é ½ diâmetro d ou r \u003d d/2.
- A partir daqui: s \u003d 4*π*r² → s \u003d 4*π*(d/2) ² → s \u003d (4π)*(d²/4) → s \u003d (4πd²)/4 → S \u003d πD.².
Ou
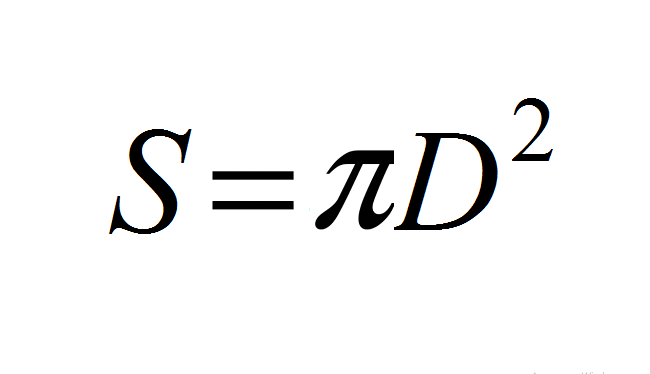
Exemplos de cálculo da área da superfície, esfera da bola, através do raio e diâmetro da bola: Descrição
Tarefa 4.
Tarefa 5.
Tarefa 6.
Como encontrar o volume da bola na área da superfície da bola, esfera: um exemplo de resolução de um problema
Tarefa 7.
Tarefa 8.
VÍDEO: Use matemática. O volume e a área da superfície dos corpos de rotação.
