Jak rozwiązać ruchy ruchu? Wzór zależności między prędkością, czasem i odległością. Zadania i rozwiązania.
Treść
- Wzór zależności czasu, prędkości i odległości w 4 klasie: jaka jest prędkość, czas, odległość?
- Jak znaleźć czas, znając prędkość i odległość?
- Jak znaleźć prędkość, jeśli jest znany czas i odległość?
- Jak znaleźć odległość, jeśli czas i prędkość są znane?
- Wykres prędkości ciała na czas: zdjęcie
- Tabela 4 Klasa: prędkość, czas, odległość
- Przykłady rozwiązywania problemów prędkości, czasu, odległości dla klasy 4
- Wideo: Zadania ruchowe
Wzór zależności czasu, prędkości i odległości w 4 klasie: jaka jest prędkość, czas, odległość?
Ludzie, zwierzęta lub samochody mogą poruszać się z pewną prędkością. Przez pewien czas mogą pójść określoną ścieżką. Na przykład: dzisiaj możesz dotrzeć do szkoły za pół godziny. Idziesz z pewną prędkością i pokonujesz 1000 metrów w 30 minut. Ścieżka, która jest pokonana, jest oznaczona w matematyce przez list S.. Prędkość jest wskazana przez list v. A czas, dla którego odrzucono ścieżkę, jest wskazany przez list t.
- Droga - S.
- Prędkość- v
- Czas - t
Jeśli spóźniłeś się do szkoły, możesz iść w ten sam sposób za 20 minut, zwiększając prędkość. Tak więc tę samą ścieżkę można podróżować w różnych czasach i przy różnych prędkościach.
Jak czas przejścia zależy od prędkości?
Im większa prędkość, tym szybsza zostanie odległość. Im niższa prędkość, tym więcej czasu musisz przejść ścieżkę.

Jak znaleźć czas, znając prędkość i odległość?
Aby znaleźć czas, który musisz przejść ścieżkę, musisz znać odległość i prędkość. Jeśli odległość zostanie podzielona na prędkość, dowiesz się czasu. Przykład takiego zadania:
Zadanie zająca. Zając uciekło od wilka z prędkością 1 kilometra na minutę. Pobiegł do swojej dziury 3 kilometry. Na którą godzinie zająca dotarła do dziury?

Jak łatwo rozwiązać problemy ruchu, gdzie musisz znaleźć odległość, czas lub prędkość?
- Uważnie przeczytaj zadanie i określ, co wiadomo z warunków problemu.
- Napisz te dane w projekcie.
- Napisz także to, co jest nieznane i co należy znaleźć
- Użyj formuły do \u200b\u200bzadań dotyczących odległości, czasu i prędkości
- Wprowadź znane dane w formule i rozwiąż problem
Rozwiązanie problemu o zając i wilka.
- Z warunków problemu ustalamy, że znamy prędkość i odległość.
- Ponadto, na podstawie warunków problemu, ustalamy, że musimy znaleźć czas, którego zając potrzebne do dotarcia do dziury.

Piszemy na przykład do projektu tych danych:
Odległość do otworu - 3 kilometry
Prędkość zając - 1 kilometr w 1 minutę
Czas jest nieznany
Teraz piszemy to samo co znaki matematyczne:
S. - 3 kilometry
V - 1 km/min
t — ?
Przypominamy sobie i piszemy formułę, aby znaleźć czas w notatniku:
t \u003d s: v
Teraz zapisujemy rozwiązanie problemu z liczbami:
t \u003d 3: 1 \u003d 3 minuty
Jak znaleźć prędkość, jeśli jest znany czas i odległość?
Aby znaleźć prędkość, jeśli czas i odległość są znane, odległość należy na chwilę podzielić. Przykład takiego zadania:
Zając uciekł od wilka i pobiegł do jego dziury 3 kilometry. Pokonał ten odległość w 3 minuty. Z jaką prędkością zajął?
Rozwiązanie problemu ruchu:
- W szkicu zapisujemy, że znamy odległość i czas.
- Na podstawie warunków problemu ustalamy, co należy znaleźć prędkość
- Pamiętaj o formule do znajdowania prędkości.
Formuły do \u200b\u200brozwiązywania takich problemów pokazano na poniższym zdjęciu.
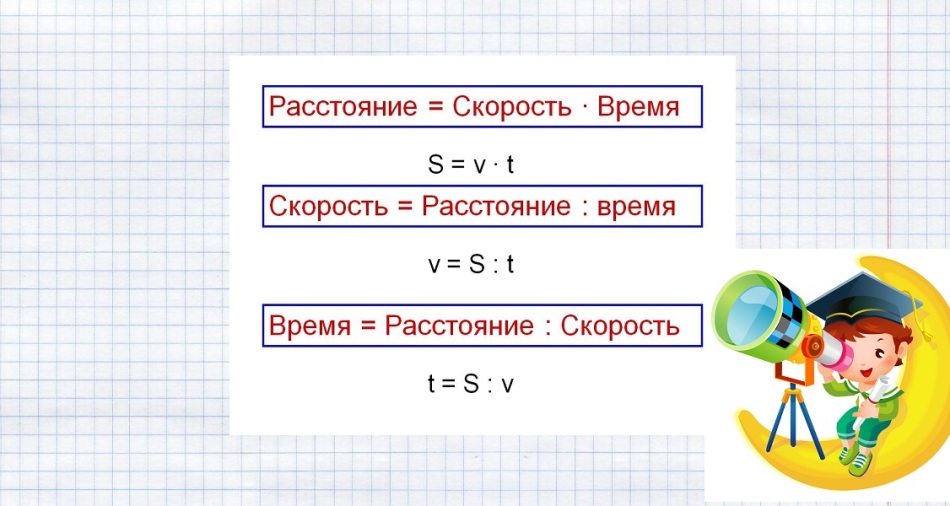
Zastępujemy znane dane i rozwiązujemy problem:
Odległość do otworu - 3 kilometry
Czas, dla którego zająca dotarła do otworu, wynosi 3 minuty
Prędkość jest nieznana
Piszemy te znane dane ze znakami matematycznymi
S. - 3 kilometry
t - 3 minuty
v -?
Zapisz formułę, aby znaleźć prędkość
v \u003d s: t
Teraz zapisujemy rozwiązanie problemu z liczbami:
v \u003d 3: 3 \u003d 1 km/min

Jak znaleźć odległość, jeśli czas i prędkość są znane?
Aby znaleźć odległość, jeśli jest znany czas i prędkość, konieczne jest pomnożenie przez prędkość. Przykład takiego zadania:
Zając uciekł od wilka z prędkością 1 kilometra w 1 minutę. Ubieganie się do dziury zajęło mu trzy minuty. W jakiej odległości zajął?
Rozwiązanie problemu: piszemy do szkicu, który znamy z warunków problemu:
Prędkość zając - 1 kilometr w 1 minutę
Czas, w którym zając uciekł do Nory, wynosi 3 minuty
Odległość jest nieznana
Teraz napiszemy to samo ze znakami matematycznymi:
v - 1 km/min
t - 3 minuty
S -?
Pamiętaj o formule znalezienia odległości:
S \u003d v ⋅ t
Teraz zapisujemy rozwiązanie problemu z liczbami:
S \u003d 3 ⋅ 1 \u003d 3 km

Jak nauczyć się rozwiązywać bardziej złożone problemy?
Aby dowiedzieć się, jak rozwiązać bardziej złożone zadania, musisz zrozumieć, w jaki sposób proste zadania są rozwiązywane, pamiętaj, jakie oznaki wskazane są odległość, prędkość i czas. Jeśli nie można zapamiętać formuł matematycznych, należy je zapisać na kartce papieru i zawsze trzymaj się pod ręką podczas rozwiązywania problemów. Rozwiąż swoje dziecko proste zadania, które można wymyślić w drodze, na przykład podczas spaceru.

Jednostki
Kiedy rozwiązują problemy związane z prędkością, czasem i odległością, często popełniają błąd, ponieważ zapomnieli przetłumaczyć jednostki pomiaru.
Ważne: jednostki pomiaru mogą być dowolne, ale jeśli istnieją różne jednostki pomiarów w jednym zadaniu, przetłumacz je tak samo. Na przykład, jeśli prędkość jest mierzona w kilometrach na minutę, wówczas odległość musi być prezentowana w kilometrach i czasu w kilka minut.
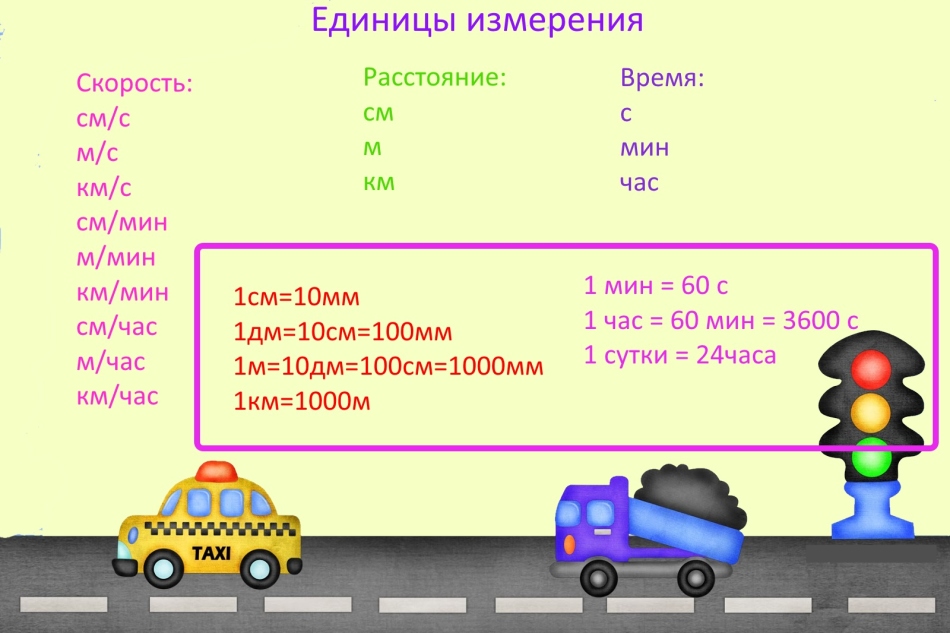
Dla ciekawych: Ogólnie akceptowany system miar nazywa się teraz metryką, ale nie zawsze tak było, aw dawnych czasach w innych jednostkach wymiaru Rus zastosowano.

Zadanie BOAS: Słoń i małpa zmierzyli długość zwężenia Boa za pomocą kroków. Podeszli do siebie. Prędkość małpy wynosiła 60 cm w ciągu jednej sekundy, a prędkość słonia wynosi 20 cm w ciągu jednej sekundy. Spędzili 5 sekund na pomiarach. Jaka jest długość obwodu BOA? (Decyzja pod zdjęciem)

Decyzja:
Na podstawie warunków problemu ustalamy, że znamy prędkość małpy i słonia oraz czas, w którym musieli zmierzyć długość wzmocnienia.
Zapisujemy te dane:
Małpa - 60 cm/s
Prędkość słonia - 20 cm/s
Czas - 5 sekund
Odległość jest nieznana
Piszemy te dane ze znakami matematycznymi:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 sekund
S -?
Napiszmy formułę odległości, jeśli znana są prędkość i czas:
S \u003d v ⋅ t
Obliczamy, w jaki sposób odległość minęła małpa:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Teraz obliczmy, ile minął słonia:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Podsumowujemy odległość, jaką minęła małpa i odległość, którą słonia:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
Wykres prędkości ciała na czas: zdjęcie
Odległość pokonana za pomocą różnych prędkości jest pokonana w różnych czasach. Im większa prędkość, tym mniej czasu.
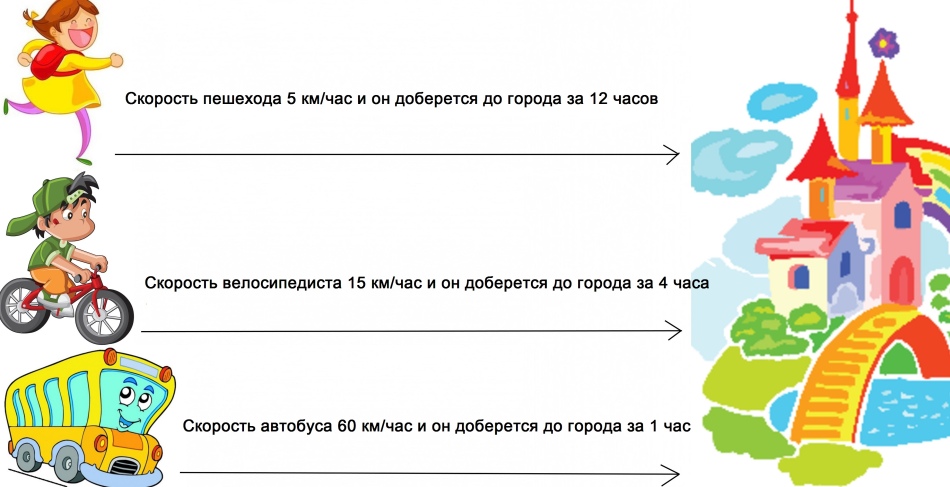
Tabela 4 Klasa: prędkość, czas, odległość
Poniższa tabela pokazuje dane, dla których musisz wymyślić problemy, a następnie je rozwiązać.
| № | Prędkość (km/godzina) | Czas (godzina) | Odległość (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Możesz fantazjować i wymyślić zadania dla stołu. Poniżej znajdują się nasze opcje zadań:
- Mama wysłała czerwonego kapelusza do babci. Dziewczyna była ciągle rozpraszana i powoli spacerowała przez las, z prędkością 5 km/h. Spędziła 2 godziny na ścieżce. W jakiej odległości minęła czerwona czapka w tym czasie?
- Postman Pechkin bierze paczkę na rowerze z prędkością 12 km/h. Wie, że odległość między jego domem a domem wuja Fedora wynosi 12 km. Pomóż Pechkin obliczyć, jak długo to potrwa droga?
- Tata Ksyusha kupił samochód i postanowił zabrać swoją rodzinę na morze. Samochód jechał z prędkością 60 km/h, a 4 godziny spędzono na drodze. Jaka jest odległość między domem Ksyusha a wybrzeżem morskim?
- Kaczki zebrały się w klinie i poleciały na ciepłe krawędzie. Ptaki machały skrzydłami zmęczeni przez 3 godziny i pokonały w tym czasie 300 km. Jaka była prędkość ptaków?
- Samoloty AN-2 leci z prędkością 220 km/h. Wyleciał z Moskwy i leci do Nizhny Nowogrod, odległość między tymi dwoma miastami wynosi 440 km. Jak długo będzie trwał samolot?

Odpowiedzi na powyższe zadania można znaleźć w poniższej tabeli:
| № | Prędkość (km/godzina) | Czas (godzina) | Odległość (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Przykłady rozwiązywania problemów prędkości, czasu, odległości dla klasy 4
Jeśli w jednym zadaniu jest kilka obiektów ruchu, musisz nauczyć dziecko rozważenia ruchu tych obiektów osobno i tylko razem. Przykład takiego zadania:
Dwóch przyjaciół Vadika i temat postanowili spacerować i opuścić swoje domy do siebie. Vadik jechał rowerem, a temat był chodzony. Vadik jechał z prędkością 10 km/h, a temat miał prędkość 5 km na godzinę. Godzina później się poznali. Jaka jest odległość między domami i tematami Vadika?
Problem ten można rozwiązać za pomocą wzoru dla zależności odległości od prędkości i czasu.
S \u003d v ⋅ t
Odległość, którą przejechał Vadik na rowerze, będzie równa jego prędkości pomnożonej przez podróż.
S \u003d 10 ⋅ 1 \u003d 10 kilometrów
Odległość, którą przeszedł temat, jest uważany za podobnie:
S \u003d v ⋅ t
Zastępujemy cyfrowe wartości jego prędkości i czasu na formułę
S \u003d 5 ⋅ 1 \u003d 5 kilometrów
Odległość, którą przejechał Vadik, należy dodać do odległości, który przeszedł temat.
10 + 5 \u003d 15 kilometrów
Jak nauczyć się rozwiązywać złożone problemy, w celu rozwiązywania tego, co musisz myśleć logicznie?
Aby rozwinąć logiczne myślenie dziecka, musisz rozwiązać z nim proste, a następnie złożone logiczne problemy. Zadania te mogą składać się z kilku etapów. Możliwe jest przejście z jednego etapu do drugiego, jeśli poprzedni jest rozwiązany. Przykład takiego zadania:
Anton poszedł na rower z prędkością 12 km/h, a Lisa jechała na skuter z prędkością 2 razy mniej niż w Anton, a Denis chodził z prędkością 2 razy mniej niż w Lisie. Jaka jest prędkość Denisa?
Aby rozwiązać ten problem, musisz najpierw dowiedzieć się prędkości Lisy i dopiero po prędkości Denisa.

Czasami w podręcznikach dla 4 klasy są trudne zadania. Przykład takiego zadania:
Dwóch rowerzystów pozostawiło wobec siebie różne miasta. Jeden z nich pospieszył i ścigał się z prędkością 12 km/h, a drugi jechał powoli z prędkością 8 km/h. Odległość między miastami, z których rowerzyści zostawili 60 km. Jaką odległość przejdzie każdy rowerzysta, zanim się spotka? (Decyzja na zdjęciu)

Decyzja:
- 12+8 \u003d 20 (km/h) to całkowita prędkość dwóch rowerzystów lub prędkość, z jaką się ze sobą zbliżyli
- 60 : 20 \u003d 3 (godziny) - To jest czas, przez który spotkali się rowerzyści
- 3 ⋅ 8 \u003d 24 (km) to odległość, którą prowadził pierwszy rowerzysta
- 12 ⋅ 3\u003d 36 (km) to odległość, którą prowadził drugi rowerzysta
- Sprawdź: 36+24 \u003d 60 (km) to odległość, którą dwóch podróżowało dwóch rowerzystów.
- Odpowiedź: 24 km, 36 km.
Zaoferuj dzieciom w postaci gry, aby rozwiązać takie problemy. Być może sami będą chcieli skomponować swoje zadanie dotyczące przyjaciół, zwierząt lub ptaków.







