ბურთის სრული ზედაპირის მოცულობისა და ფართობის ფორმულა, სფერო რადიუსის მეშვეობით და ბურთის დიამეტრით: მნიშვნელობა. ბურთის ზედაპირისა და მოცულობის გაანგარიშების მაგალითები, ბურთის რადიუსისა და დიამეტრის მეშვეობით: აღწერა. როგორ მოვძებნოთ ბურთის მოცულობა ბურთის ზედაპირის ფართობის მეშვეობით: მაგალითი

სტატია სასარგებლო იქნება სკოლის მოსწავლეებისა და მომავალი განმცხადებლებისთვის, რომლებიც ემზადებიან გამოცდისთვის.

ბურთის მოცულობის ფორმულა რადიუსის მეშვეობით: მნიშვნელობა

ბურთის V მოცულობა გამოითვლება ფორმულით (იხ

ეს ფორმულა არის ბაზა!

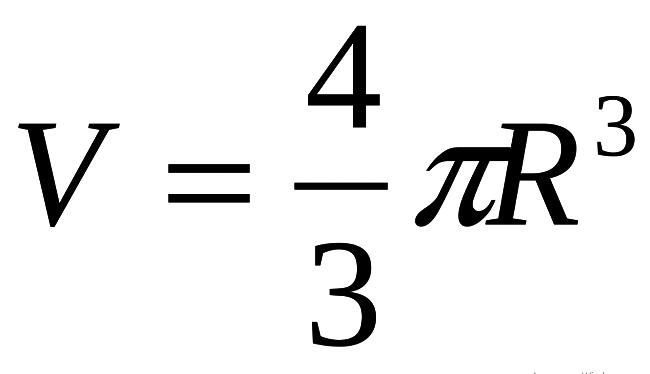
ბურთის მოცულობის ფორმულა დიამეტრის მეშვეობით: მნიშვნელობა

1. გამოიყენეთ ბაზის ფორმულა: v \u003d 4/3*π*r³.
2. რადიუსი R არის ½ დიამეტრი D ან r \u003d d/2.
3. აქედან გამომდინარე: v \u003d 4/3*π*r³ → v \u003d (4π/3)*(d/2) ³ → v \u003d (4π/3)*(d³/8) → V \u003d πდ.³/6.

ან

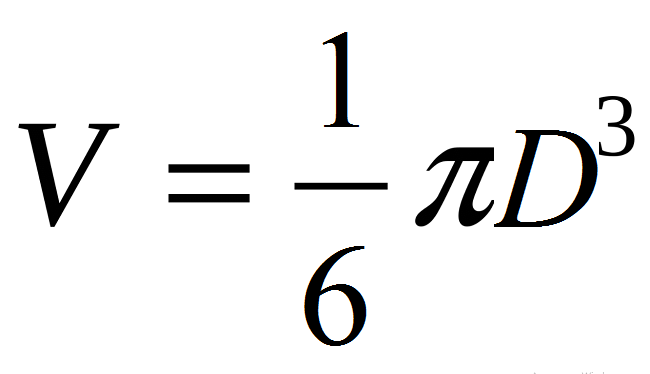
ბურთის მოცულობის გაანგარიშების მაგალითები, რადიუსის მეშვეობით და ბურთის დიამეტრით: აღწერა

დავალება 1.

ბურთის რადიუსი 10 სმ. იპოვნეთ მისი მოცულობა.

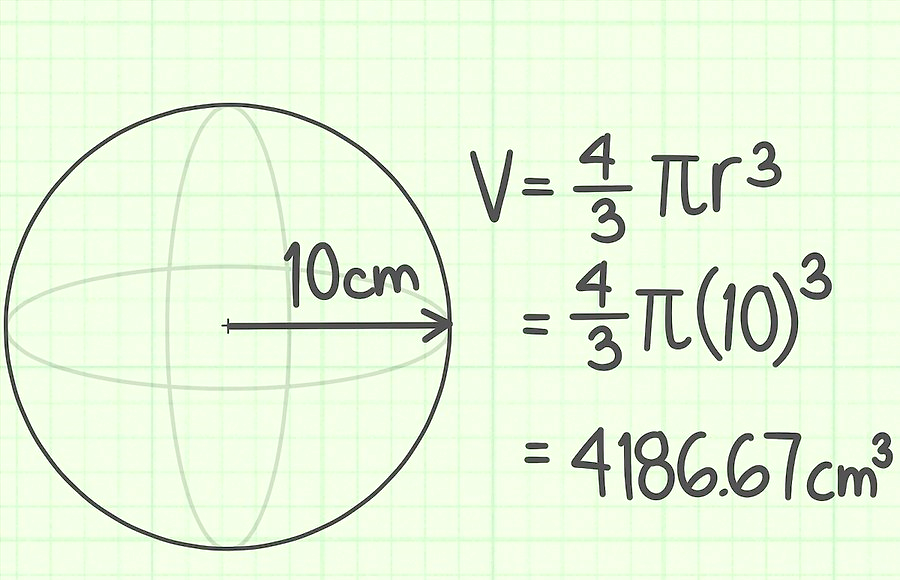
დავალება 2.

ბურთის დიამეტრი 10 სმ. იპოვნეთ მისი მოცულობა.

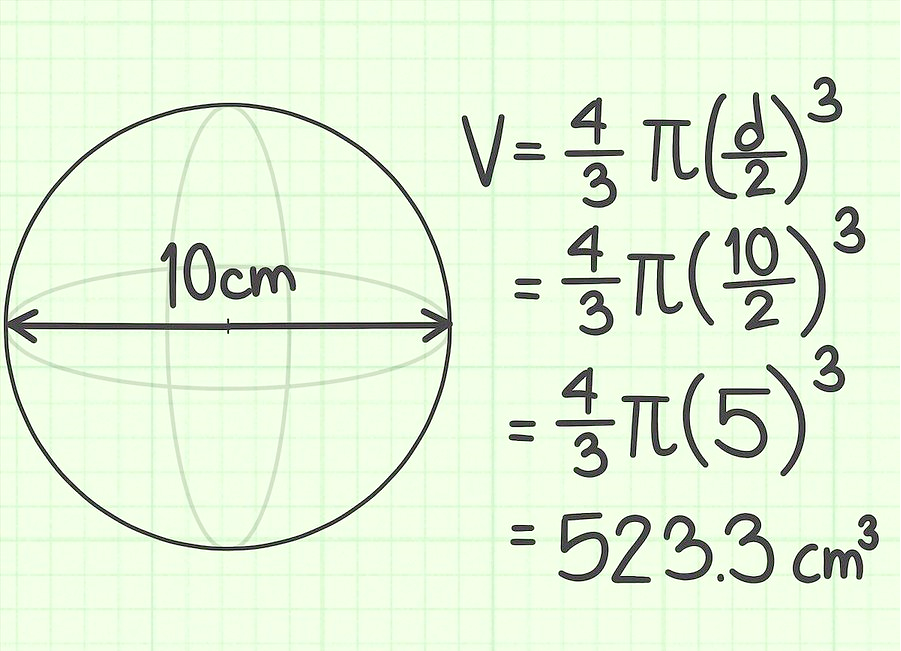
დავალება 3.

მთვარის დიამეტრის თანაფარდობა და დედამიწის დიამეტრი 1: 4. რამდენჯერ არის დედამიწის მოცულობა უფრო მეტი, ვიდრე მთვარის მოცულობა?

გამოსავალი:

პასუხი: 64 ჯერ.

Მნიშვნელოვანი: არსებობს მრავალი ონლაინ კალკულატორი, რომელიც საშუალებას გაძლევთ სწრაფად იპოვოთ მოცემული მნიშვნელობა. მაგალითად, მომსახურება ვებგვერდი.

ბურთის სრული ზედაპირის ფორმულა, სფერო რადიუსის მეშვეობით: მნიშვნელობა

სფეროს/ბურთის ზედაპირის ფართობი გამოითვლება ფორმულის მიხედვით (იხ

ეს ფორმულა არის ბაზა!

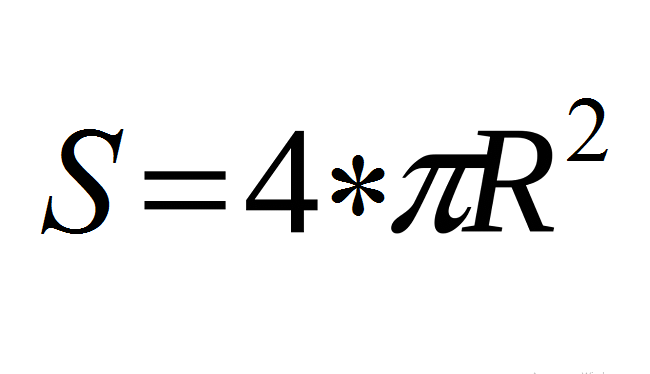
ბურთის სრული ზედაპირის ფორმულა, სფერო დიამეტრის მეშვეობით: მნიშვნელობა

1. გამოიყენეთ ბაზის ფორმულა: s \u003d 4*π*r².
2. რადიუსი R არის ½ დიამეტრი D ან r \u003d d/2.
3. აქედან: s \u003d 4*π*r² → s \u003d 4*π*(d/2) ² → s \u003d (4π)*(d²/4) → s \u003d (4πd²)/4 → S \u003d πდ.².

ან

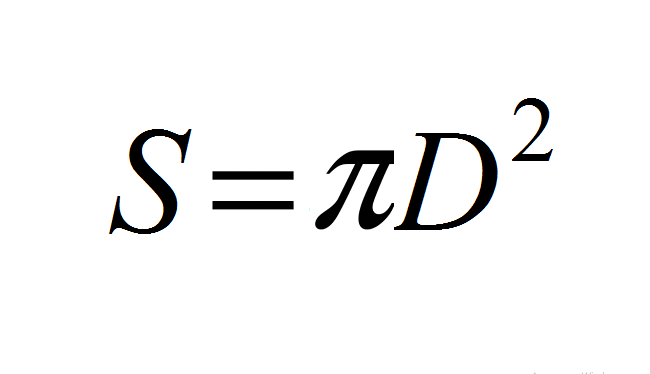
ზედაპირის ფართობის, ბურთის სფეროს გაანგარიშების მაგალითები, ბურთის რადიუსისა და დიამეტრის მეშვეობით: აღწერა

დავალება 4.

დავალება 5.

დავალება 6.

როგორ მოვიძიოთ ბურთის მოცულობა ბურთის ზედაპირის ფართობის მეშვეობით, სფერო: პრობლემის გადაჭრის მაგალითი

დავალება 7.

დავალება 8.

ვიდეო: გამოიყენეთ მათემატიკა. ბრუნვის სხეულების ზედაპირის მოცულობა და ფართობი.