Comment trouver une zone carrée si le périmètre est connu, diagonale? Comment trouver le carré du carré inscrit dans le cercle et décrit près de la circonférence: formule, exemples de problèmes de résolution. Comment trouver le côté et la diagonale du carré, si sa zone est connue?

Lisez l'article pour savoir comment trouver la zone carrée de différentes manières.

Contenu

Un carré est un rectangle équilatéral. Ce quadrilatère approprié et plat a l'égalité de tous les côtés, coins et diagonales. En raison du fait qu'il existe une telle égalité, la formule de calcul de la zone et d'autres caractéristiques est légèrement modifiée par rapport aux autres chiffres mathématiques. Mais cela ne rend pas les tâches trop compliquées. Analysons toutes les formules et solutions à cet article.

Comment trouver le côté du carré, en connaissant sa zone?

Carré S. Les carrés directs et carrés sont calculés par la formule: un Multiplier par b.. Mais comme le carré a une égalité complète des parties, sa superficie sera égale: S \u003d (a) au deuxième degré.Comment découvrir la taille du côté du carré, en connaissant sa zone?

Si la surface du carré est connue, nous trouvons le côté en calculant la zone sous la racine carrée.
Par exemple, la zone du carré est 49, alors à quoi est le côté égal?
49 \u003d (a) au deuxième degré. La solution: a \u003d racine de 49 \u003d 7. Réponse: 7.

Si vous devez trouver le côté du carré carré, dont la zone est trop longue, utilisez la calculatrice. Composez d'abord le numéro de la zone, puis appuyez sur le panneau racine sur le clavier de la calculatrice. Le numéro résultant sera la réponse.

Comment trouver une diagonale carrée si sa zone est connue?

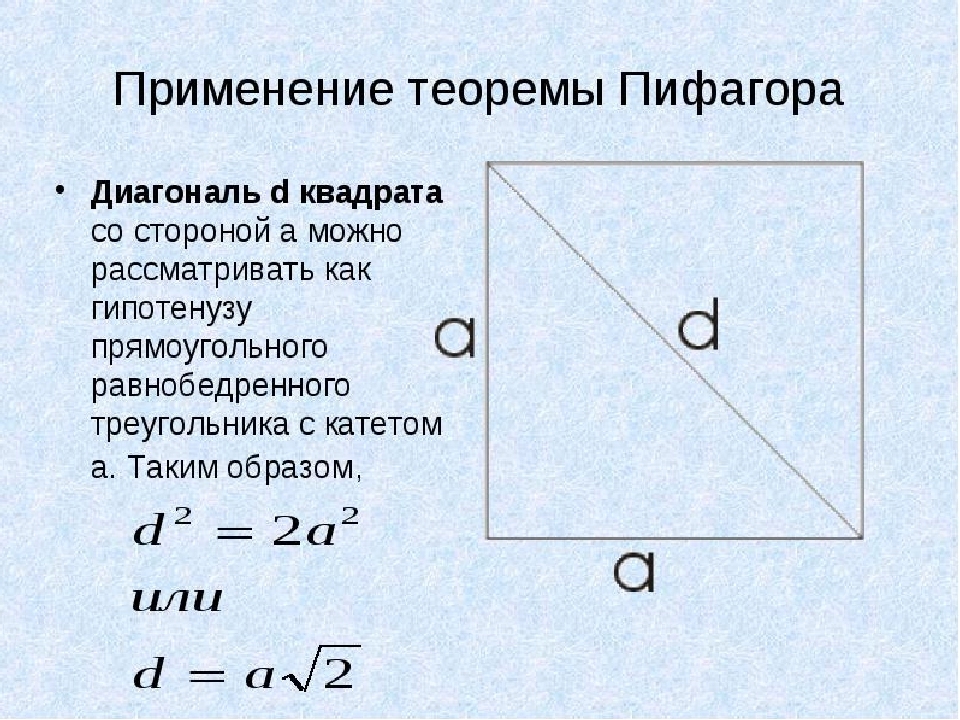
Dans cet exemple, nous utiliserons le théorème de Pythagore. Dans un carré, tous les côtés sont égaux, et la diagonale rÉ. Nous considérerons l'hypoténuse d'un triangle isocèle rectangulaire avec une jambe un. Maintenant, nous trouvons une diagonale carrée si sa zone est connue:

Afin de ne pas peindre l'intégralité du théorème de Pythagore, nous déciderons de la deuxième option: d \u003d Aising, où A est le côté du carré.
Donc, nous connaissons la zone du carré, par exemple, elle est égale à 64. Donc un côté a \u003d √64 \u003d 8.
Il s'avère D \u003d 8√2. La racine de 2 ne se déroule pas tout le nombre, donc dans la réponse, vous pouvez écrire de cette façon: d \u003d 8√2. Mais, si vous souhaitez calculer la valeur, utilisez la calculatrice: √2 \u003d 1,41421356237 et multiplier par 8, il s'avère 11, 3137084.

Important: En règle générale, en mathématiques, aucun nombre avec un grand nombre de nombres ne reste en réponse. Il est nécessaire de se rond ou de partir avec la racine. Par conséquent, la réponse à la diagonale est si la zone est 64 comme suit: d \u003d 8√2.

Comment trouver une zone carrée à travers une diagonale?

La formule pour trouver la zone carrée à travers la diagonale est simple:

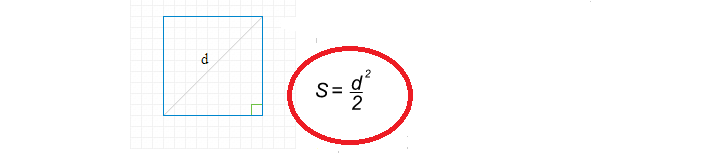
Maintenant, écrivons une solution pour trouver la zone carrée à travers la diagonale:

Diagonal d \u003d 8.
8 sur le carré est 64.
64 Diviser par 2 égal 32.
La zone carrée est de 32.

Conseils: Cette tâche a une autre solution à travers le théorème de Pythagore, mais elle est plus complexe. Par conséquent, utilisez la solution que nous avons examinée.

Comment trouver une zone carrée, connaissant son périmètre?

Le périmètre du carré P. - C'est la somme de toutes les parties. Pour trouver sa zone, en connaissant son périmètre, vous devez d'abord calculer le côté du carré. La solution:

Supposons que le périmètre soit 24. Divisez 24 en 4 côtés, il s'avère que 6 - c'est un côté.
Maintenant, nous utilisons la formule pour trouver la zone, sachant ce que le côté carré est égal: S \u003d a dans un carré, s \u003d 6 dans un carré \u003d 36.
Réponse: 36

Comme vous pouvez le voir, connaître le périmètre du carré, il suffit de trouver sa zone.

Comment trouver une zone d'un carré inscrit dans un cercle avec un rayon donné?

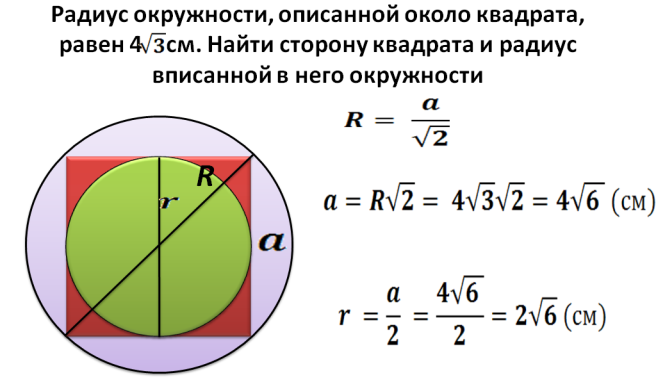
Rayon R - C'est la moitié de la diagonale d'un carré inscrit dans un cercle. Maintenant, nous pouvons trouver une diagonale par la formule: d \u003d 2 * r. Ensuite, nous trouvons le carré du carré inscrit dans un cercle avec un rayon donné:

La diagonale est 2 multipliée par le rayon. Par exemple, le rayon est 5, alors la diagonale est égale 2*5=10.
Il a été décrit ci-dessus comment trouver le carré du carré si la diagonale est connue: S \u003d diagonale dans un carré divisé en 2. S \u003d 10 * 10 et diviser par 2 \u003d 50.
Réponse - 50.

Cette tâche est un peu plus compliquée, mais aussi facilement résolue si vous connaissez toutes les formules.

Comment trouver une zone d'un carré décrit près d'un cercle avec un rayon donné?

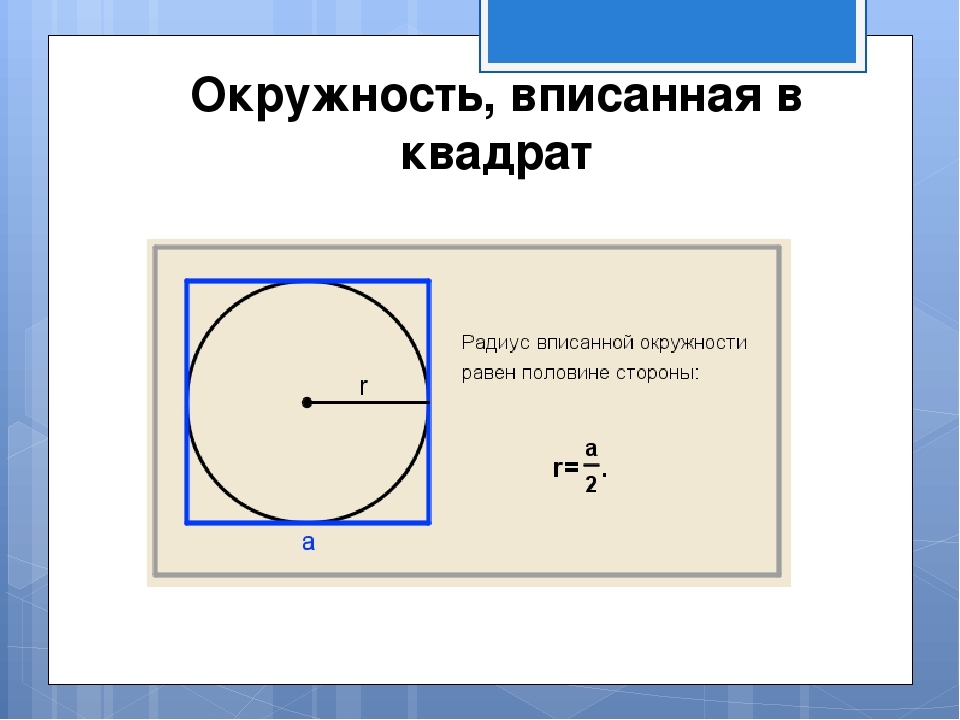
L'image montre que le rayon du cercle inscrit est égal à la moitié du côté. Le côté est situé en fonction de la formule inversée qui représente dans l'image: a \u003d 2 * r. Ensuite, nous trouvons la zone du carré décrit près du cercle avec un rayon donné selon la formule S \u003d et dans un carré. La solution:

Supposons que le rayon soit 7. Le côté du carré A est 2 * 7 \u003d 14.
S \u003d 14 dans un carré \u003d 196.

Si vous comprenez l'essence de la résolution de tels problèmes, vous pouvez les résoudre rapidement et simplement. Regardons quelques exemples de plus.

Exemples de résolution de problèmes sur le sujet "carré carré"

Pour réparer le matériau couvert et se souvenir de toutes les formules, il est nécessaire de résoudre plusieurs exemples de problèmes sur le thème de la «zone carrée». Nous commençons par une tâche simple et passons à la résolution plus complexe:

Exemples de résolution de problèmes sur le sujet de la zone carrée

Exemples de résolution de problèmes complexes sur le sujet "carré carré"

Vous savez maintenant comment utiliser la formule pour le carré du carré, ce qui signifie que vous pouvez faire n'importe quelle tâche. Succès dans la formation future!