Comment résoudre les mouvements du mouvement? La formule de dépendance entre la vitesse, le temps et la distance. Tâches et solutions.
Contenu
- La formule pour la dépendance du temps, de la vitesse et de la distance sur la 4e année: comment est la vitesse, le temps, la distance?
- Comment trouver du temps, connaître la vitesse et la distance?
- Comment trouver la vitesse si le temps et la distance sont connus?
- Comment trouver une distance si le temps et la vitesse sont connus?
- Graphique de la vitesse corporelle à l'heure: Photo
- Tableau 4 Classe: vitesse, temps, distance
- Exemples de résolution de problèmes pour la vitesse, le temps, la distance pour la 4e année
- Vidéo: Tâches de mouvement
La formule pour la dépendance du temps, de la vitesse et de la distance sur la 4e année: comment est la vitesse, le temps, la distance?
Les personnes, les animaux ou les voitures peuvent se déplacer à une certaine vitesse. Pendant un certain temps, ils peuvent suivre un certain chemin. Par exemple: aujourd'hui, vous pouvez atteindre votre école dans une demi-heure. Vous allez à une certaine vitesse et surmontez 1000 mètres en 30 minutes. Le chemin qui est surmonté est désigné en mathématiques par la lettre S.. La vitesse est indiquée par la lettre v. Et le temps pour lequel le chemin a été refusé est indiqué par la lettre t.
- Chemin - S.
- Vitesse - V
- Temps - t
Si vous êtes en retard à l'école, vous pouvez aller de la même manière en 20 minutes, augmentant votre vitesse. Ainsi, le même chemin peut être parcouru à différents moments et à différentes vitesses.
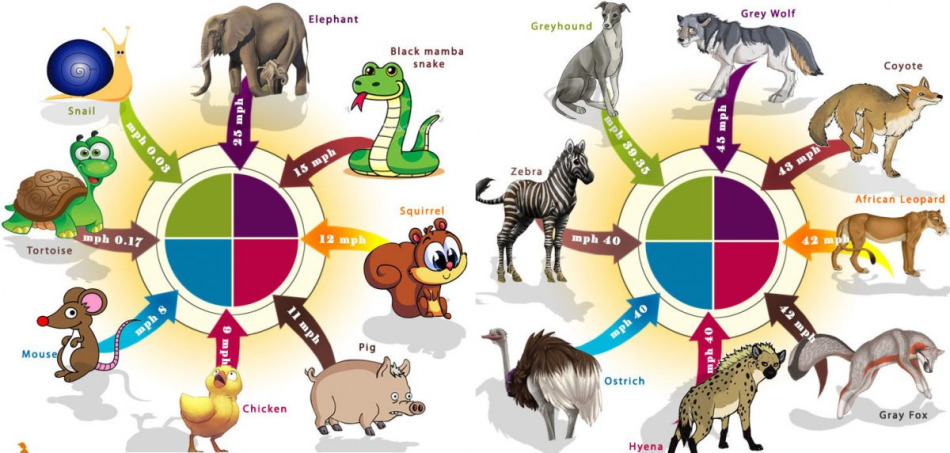
Comment le temps de passage dépend-il de la vitesse?
Plus la vitesse est grande, plus la distance sera effectuée rapide. Et plus la vitesse est faible, plus vous avez besoin de temps pour passer le chemin.

Comment trouver du temps, connaître la vitesse et la distance?
Afin de trouver le temps dont vous devez passer le chemin, vous devez connaître la distance et la vitesse. Si la distance est divisée en vitesse, vous découvrirez le temps. Un exemple d'une telle tâche:
La tâche du lièvre. Le lièvre s'est éloigné du loup à une vitesse de 1 kilomètre par minute. Il a couru vers son trou de 3 kilomètres. Pour quelle heure le lièvre a-t-il atteint un trou?

Comment est-il facile de résoudre les problèmes de mouvement, où vous devez trouver une distance, un temps ou une vitesse?
- Lisez soigneusement la tâche et déterminez ce qui est connu dans les conditions du problème.
- Écrivez ces données sur le projet.
- Écrivez également ce qui est inconnu et ce qui doit être trouvé
- Utilisez la formule pour les tâches sur la distance, le temps et la vitesse
- Entrez les données connues dans la formule et résolvez le problème
Solution pour le problème sur le lièvre et le loup.
- D'après les conditions du problème, nous déterminons que nous connaissons la vitesse et la distance.
- De plus, à partir des conditions du problème, nous déterminons que nous devons trouver le temps dont le lièvre avait besoin pour atteindre le trou.

Nous écrivons au projet de ces données par exemple:
Distance au trou - 3 kilomètres
Vitesse de lièvre - 1 kilomètre en 1 minute
Le temps est inconnu
Maintenant, nous écrivons la même chose que les signes mathématiques:
S. - 3 kilomètres
V - 1 km / min
t — ?
Nous rappelons et écrivons une formule pour trouver l'heure dans le cahier:
t \u003d s: v
Maintenant, nous écrivons la solution du problème avec les nombres:
t \u003d 3: 1 \u003d 3 minutes
Comment trouver la vitesse si le temps et la distance sont connus?
Afin de trouver la vitesse, si le temps et la distance sont connus, la distance doit être divisée pendant un certain temps. Un exemple d'une telle tâche:
Le lièvre s'est éloigné du loup et a couru vers son trou de 3 kilomètres. Il a surmonté cette distance en 3 minutes. À quelle vitesse le lièvre a-t-il fonctionné?
Résoudre le problème du mouvement:
- Dans le projet, nous écrivons que nous connaissons la distance et le temps.
- D'après les conditions du problème, nous déterminons ce qui doit être trouvé
- N'oubliez pas la formule pour trouver la vitesse.
Les formules pour résoudre ces problèmes sont présentées dans l'image ci-dessous.
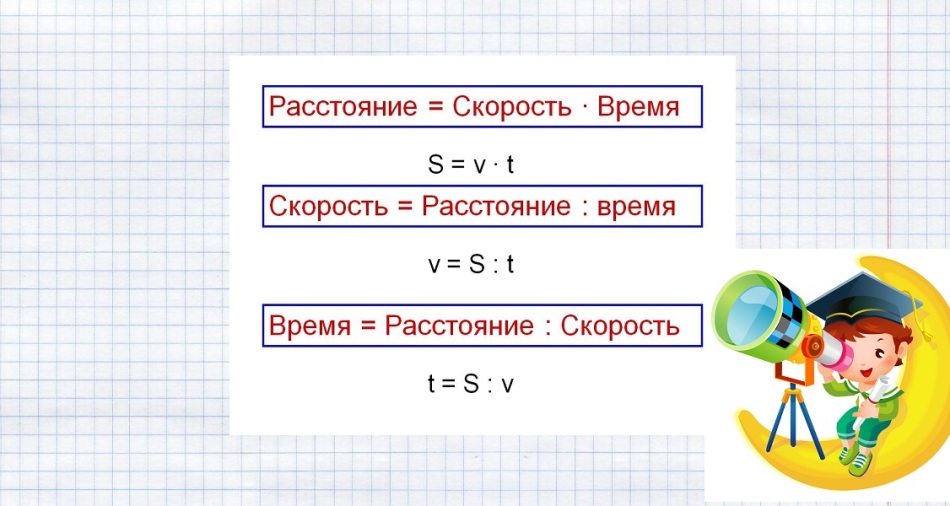
Nous substituons les données connues et résolvons le problème:
Distance au trou - 3 kilomètres
Le temps pour lequel le lièvre a atteint le trou est de 3 minutes
La vitesse est inconnue
Nous écrivons ces données connues avec des signes mathématiques
S. - 3 kilomètres
t - 3 minutes
v -?
Enregistrez la formule pour trouver la vitesse
v \u003d s: t
Maintenant, nous écrivons la solution du problème avec les nombres:
v \u003d 3: 3 \u003d 1 km / min

Comment trouver une distance si le temps et la vitesse sont connus?
Pour trouver une distance, si elle est connue du temps et de la vitesse, il est nécessaire de se multiplier par vitesse. Un exemple d'une telle tâche:
Le lièvre s'est éloigné du loup à une vitesse de 1 kilomètre en 1 minute. Il lui a fallu trois minutes pour courir vers le trou. À quelle distance le lièvre a-t-il parcouru?
Solution du problème: nous écrivons à un projet que nous connaissons dans les conditions du problème:
Vitesse de lièvre - 1 kilomètre en 1 minute
Le temps où le lièvre s'est enfui à Nora est de 3 minutes
La distance est inconnue
Maintenant, nous allons écrire la même chose avec les signes mathématiques:
v - 1 km / min
t - 3 minutes
S -?
N'oubliez pas la formule pour trouver la distance:
S \u003d v ⋅ t
Maintenant, nous écrivons la solution du problème avec les nombres:
S \u003d 3 ⋅ 1 \u003d 3 km

Comment apprendre à résoudre des problèmes plus complexes?
Pour apprendre à résoudre des tâches plus complexes, vous devez comprendre à quel point les tâches sont résolues, rappelez-vous quels signes indiquent la distance, la vitesse et le temps. S'il n'est pas possible de se souvenir des formules mathématiques, ils doivent être écrits sur une feuille de papier et toujours à portée de main tout en résolvant des problèmes. Résolvez avec votre enfant des tâches simples qui peuvent être inventées en déplacement, par exemple, lors d'une promenade.

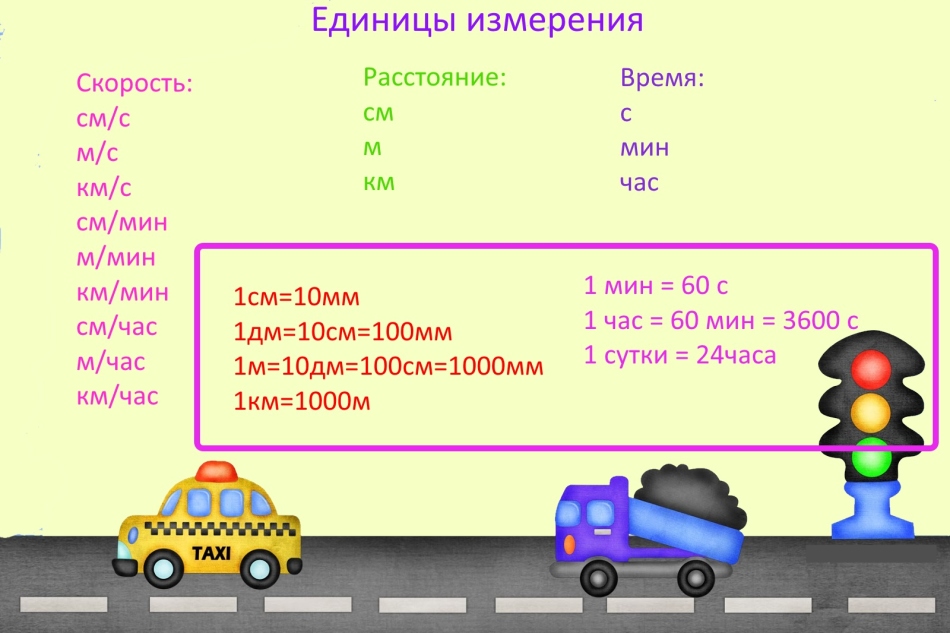
Unités
Lorsqu'ils résolvent des problèmes de vitesse, de temps et de distance, ils font souvent une erreur, car ils ont oublié de traduire des unités de mesure.
IMPORTANT: Les unités de mesure peuvent en être, mais s'il existe différentes unités de mesures dans une tâche, traduisez-les de la même manière. Par exemple, si la vitesse est mesurée en kilomètres par minute, la distance doit être présentée en kilomètres et du temps en quelques minutes.
Pour curieux: Le système de mesures généralement accepté est appelé métrique maintenant, mais ce n'était pas toujours le cas, et dans le passé en Russie, d'autres unités de dimension ont été utilisées.

La tâche des boas: L'éléphant et le singe ont mesuré la longueur du constricteur BOA avec des étapes. Ils se sont déplacés l'un vers l'autre. La vitesse du singe était de 60 cm en une seconde et la vitesse d'éléphant est de 20 cm en une seconde. Ils ont passé 5 secondes en mesure. Quelle est la longueur du boa constrictor? (Décision sous l'image)

La solution:
D'après les conditions du problème, nous déterminons que nous connaissons la vitesse du singe et de l'éléphant et le temps dont ils avaient besoin pour mesurer la longueur du coup de pouce.
Nous écrivons ces données:
Vitesse du singe - 60 cm / s
Vitesse d'éléphant - 20 cm / s
Temps - 5 secondes
La distance est inconnue
Nous écrivons ces données avec des signes mathématiques:
v1 - 60 cm / s
v2 - 20 cm / s
t - 5 secondes
S -?
Écrivons la formule pour la distance si la vitesse et le temps sont connues:
S \u003d v ⋅ t
Nous calculons à quel point le singe est passé:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Calculons maintenant combien l'éléphant a passé:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Nous résumons la distance que le singe et la distance que l'éléphant a adopté:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
Graphique de la vitesse corporelle à l'heure: Photo
La distance surmontée avec différentes vitesses est surmontée à différents moments. Plus la vitesse est grande, moins il faudra de temps.
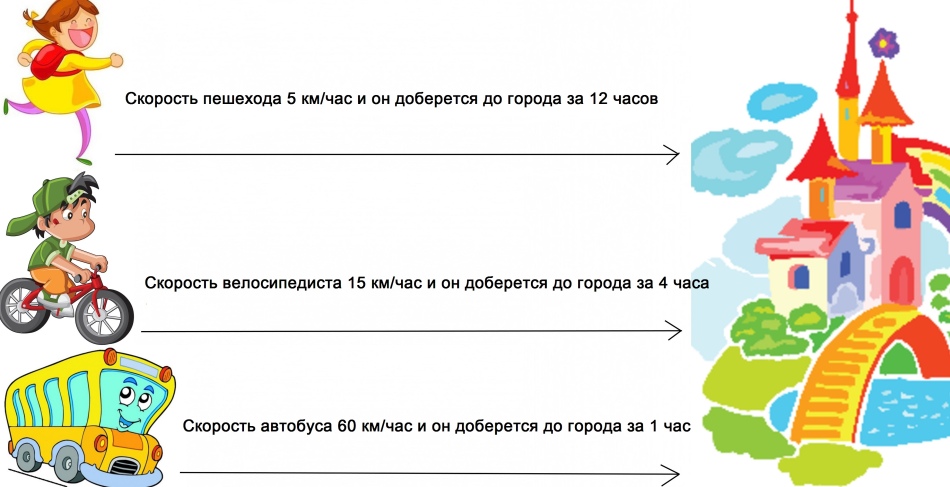
Tableau 4 Classe: vitesse, temps, distance
Le tableau ci-dessous montre les données pour lesquelles vous devez trouver des problèmes, puis les résoudre.
| № | Vitesse (km / heure) | Heure (heure) | Distance (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Vous pouvez fantasmer et trouver vous-même des tâches pour la table. Vous trouverez ci-dessous nos options pour les tâches:
- Maman a envoyé un chapeau rouge à sa grand-mère. La fille était constamment distraite et traversa lentement la forêt, à une vitesse de 5 km / h. Elle a passé 2 heures sur le chemin. Quelle distance un capuchon rouge a-t-il passé pendant cette période?
- Le Postman Pechkin prend un colis sur un vélo à une vitesse de 12 km / h. Il sait que la distance entre sa maison et la maison de l'oncle Fedor est de 12 km. Aidez Pechkin à calculer combien de temps cela prendra-t-il pour la route?
- Papa Ksyusha a acheté une voiture et a décidé d'emmener sa famille à la mer. La voiture conduisait à une vitesse de 60 km / h et 4 heures ont été passées sur la route. Quelle est la distance entre la maison de Ksyusha et la côte de la mer?
- Les canards se sont rassemblés dans le coin et ont volé dans les bords chauds. Les oiseaux ont agité leurs ailes fatiguées pendant 3 heures et ont surmonté 300 km pendant cette période. Quelle était la vitesse des oiseaux?
- L'avion AN-2 vole à une vitesse de 220 km / h. Il a volé de Moscou et vole vers Nizhny Novgorod, la distance entre ces deux villes est de 440 km. Combien de temps va l'avion?

Les réponses aux tâches ci-dessus se trouvent dans le tableau ci-dessous:
| № | Vitesse (km / heure) | Heure (heure) | Distance (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Exemples de résolution de problèmes pour la vitesse, le temps, la distance pour la 4e année
S'il y a plusieurs objets de mouvement dans une tâche, vous devez apprendre à l'enfant à considérer le mouvement de ces objets séparément et seulement alors ensemble. Un exemple d'une telle tâche:
Deux amis de Vadik et le sujet ont décidé de se promener et ont laissé leurs maisons l'un à l'autre. Vadik a conduit un vélo et le sujet marchait. Vadik a roulé à une vitesse de 10 km / h, et le sujet était à une vitesse de 5 km par heure. Une heure plus tard, ils se sont rencontrés. Quelle est la distance entre les maisons et les sujets de Vadik?
Ce problème peut être résolu en utilisant la formule pour la dépendance de la distance sur la vitesse et le temps.
S \u003d v ⋅ t
La distance que Vadik a parcourue sur un vélo sera égale à sa vitesse multipliée par les voyages.
S \u003d 10 ⋅ 1 \u003d 10 kilomètres
La distance réalisée par le sujet est considérée comme de la même manière:
S \u003d v ⋅ t
Nous substituons les valeurs numériques de sa vitesse et de son temps dans la formule
S \u003d 5 ⋅ 1 \u003d 5 kilomètres
La distance parcourue par Vadik doit être ajoutée à la distance réalisée par le sujet.
10 + 5 \u003d 15 kilomètres
Comment apprendre à résoudre des problèmes complexes, pour résoudre ce que vous devez penser logiquement?
Pour développer la pensée logique de l'enfant, vous devez résoudre avec lui des problèmes logiques simples, puis complexes. Ces tâches peuvent être composées de plusieurs étapes. Il est possible de passer d'une étape à l'autre si la précédente est résolue. Un exemple d'une telle tâche:
Anton a fait un vélo à une vitesse de 12 km / h, et Lisa est montée sur un scooter à une vitesse de 2 fois moins que celle d'Anton, et Denis a marché à une vitesse de 2 fois moins que celle de Lisa. Quelle est la vitesse de Denis?
Pour résoudre ce problème, vous devez d'abord découvrir la vitesse de Lisa et seulement après la vitesse de Denis.

Parfois, dans les manuels pour 4 grade, il y a des tâches difficiles. Un exemple d'une telle tâche:
Deux cyclistes ont laissé différentes villes l'une à l'autre. L'un d'eux se précipita et courut à une vitesse de 12 km / h, et le second a roulé lentement à une vitesse de 8 km / h. La distance entre les villes à partir desquelles les cyclistes ont quitté 60 km. À quelle distance chaque cycliste passera-t-il avant de se rencontrer? (Décision sous la photo)

La solution:
- 12 + 8 \u003d 20 (km / h) est la vitesse totale de deux cyclistes, ou la vitesse avec laquelle ils se sont approchés
- 60 : 20 \u003d 3 (heures) - C'est le moment où les cyclistes se sont rencontrés
- 3 ⋅ 8 \u003d 24 (km) est la distance que le premier cycliste a conduit
- 12 ⋅ 3\u003d 36 (km) est la distance que le deuxième cycliste a conduit
- Vérifier: 36 + 24 \u003d 60 (km) est la distance parcourue par deux cyclistes.
- Réponse: 24 km, 36 km.
Offrez aux enfants sous la forme d'un jeu pour résoudre de tels problèmes. Peut-être qu'ils voudront eux-mêmes composer leur tâche concernant les amis, les animaux ou les oiseaux.







