Wie löst ich Bewegungen für Bewegung? Die Formel der Abhängigkeit zwischen Geschwindigkeit, Zeit und Entfernung. Aufgaben und Lösungen.
Inhalt
- Die Formel für die Abhängigkeit von Zeit, Geschwindigkeit und Entfernung über die 4. Klasse: Wie ist Geschwindigkeit, Zeit, Entfernung?
- Wie finde ich Zeit, Kenntnis von Geschwindigkeit und Entfernung?
- Wie finde ich Geschwindigkeit, wenn Zeit und Entfernung bekannt sind?
- Wie finde ich eine Entfernung, wenn Zeit und Geschwindigkeit bekannt sind?
- Graph der Körpergeschwindigkeit pünktlich: Foto
- Tabelle 4 Klasse: Geschwindigkeit, Zeit, Entfernung
- Beispiele für die Lösung von Problemen für Geschwindigkeit, Zeit, Entfernung für Grad 4
- Video: Bewegungsaufgaben
Die Formel für die Abhängigkeit von Zeit, Geschwindigkeit und Entfernung über die 4. Klasse: Wie ist Geschwindigkeit, Zeit, Entfernung?
Menschen, Tiere oder Autos können sich mit einer bestimmten Geschwindigkeit bewegen. Für eine bestimmte Zeit können sie einen bestimmten Weg gehen. Zum Beispiel: Heute können Sie Ihre Schule in einer halben Stunde erreichen. Sie gehen mit einer bestimmten Geschwindigkeit und überwinden in 30 Minuten 1000 Meter. Der überwundene Weg ist in der Mathematik durch den Brief bezeichnet S.. Die Geschwindigkeit wird durch den Buchstaben angezeigt v. Und die Zeit, für die der Pfad abgelehnt wurde, wird durch den Buchstaben angezeigt t.
- Weg - S.
- Geschwindigkeit- v
- Zeit - t
Wenn Sie spät in der Schule sind, können Sie in 20 Minuten genauso gehen und Ihre Geschwindigkeit erhöhen. Der gleiche Weg kann also über verschiedene Zeiten und mit unterschiedlichen Geschwindigkeiten gereist werden.
Wie hängt die Durchgangszeit von der Geschwindigkeit ab?
Je größer die Geschwindigkeit, desto schneller wird die Entfernung gemacht. Und je niedriger die Geschwindigkeit, desto mehr Zeit müssen Sie den Weg bestehen.

Wie finde ich Zeit, Kenntnis von Geschwindigkeit und Entfernung?
Um die Zeit zu finden, die Sie für den Weg benötigen, müssen Sie die Entfernung und Geschwindigkeit kennen. Wenn die Entfernung in Geschwindigkeit unterteilt ist, werden Sie die Zeit herausfinden. Ein Beispiel für eine solche Aufgabe:
Die Aufgabe des Hase. Der Hase lief mit einer Geschwindigkeit von 1 Kilometer pro Minute vom Wolf weg. Er rannte 3 Kilometer zu seinem Loch. Zu welcher Zeit erreichte der Hase ein Loch?

Wie ist es einfach, die Probleme für die Bewegung zu lösen, wo Sie eine Entfernung, Zeit oder Geschwindigkeit finden müssen?
- Lesen Sie die Aufgabe sorgfältig durch und bestimmen Sie, was unter den Bedingungen des Problems bekannt ist.
- Schreiben Sie diese Daten zum Entwurf.
- Schreiben Sie auch, was unbekannt ist und was gefunden werden muss
- Verwenden Sie die Formel für Aufgaben über Entfernung, Zeit und Geschwindigkeit
- Geben Sie die bekannten Daten in die Formel ein und lösen Sie das Problem
Lösung für das Problem über den Hasen und den Wolf.
- Aus den Bedingungen des Problems bestimmen wir, dass wir Geschwindigkeit und Entfernung kennen.
- Aus den Bedingungen des Problems bestimmen wir auch, dass wir die Zeit finden müssen, in der der Hase das Loch erreichen musste.

Wir schreiben zum Beispiel in den Entwurf dieser Daten:
Entfernung zum Loch - 3 Kilometer
Hase -Geschwindigkeit - 1 Kilometer in 1 Minute
Zeit ist unbekannt
Jetzt schreiben wir dasselbe wie mathematische Zeichen:
S. - 3 Kilometer
V - 1 km/min
t — ?
Wir erinnern und schreiben eine Formel, um die Zeit im Notizbuch zu finden:
t \u003d s: v
Jetzt schreiben wir die Lösung des Problems mit Zahlen auf:
t \u003d 3: 1 \u003d 3 Minuten
Wie finde ich Geschwindigkeit, wenn Zeit und Entfernung bekannt sind?
Um Geschwindigkeit zu finden, muss die Entfernung für eine Weile geteilt werden, wenn Zeit und Entfernung bekannt sind. Ein Beispiel für eine solche Aufgabe:
Der Hase lief vom Wolf weg und rannte 3 Kilometer zu seinem Loch. Er überwand diesen Abstand in 3 Minuten. Mit welcher Geschwindigkeit lief der Hase?
Lösen des Bewegungsproblems:
- Im Entwurf schreiben wir auf, dass wir die Entfernung und Zeit kennen.
- Aus den Bedingungen des Problems bestimmen wir, was Geschwindigkeit gefunden werden muss
- Erinnern Sie sich an die Formel, um Geschwindigkeit zu finden.
Formeln zur Lösung solcher Probleme werden im Bild unten gezeigt.
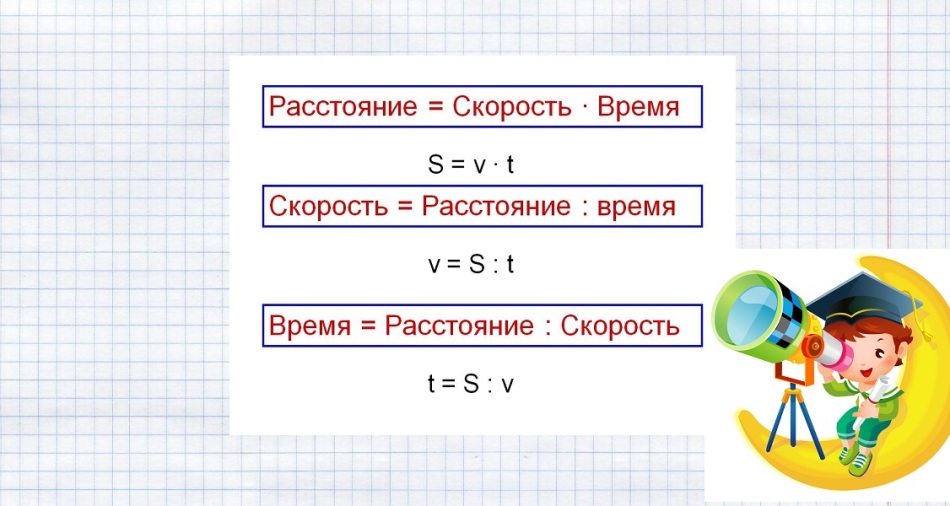
Wir ersetzen die bekannten Daten und lösen das Problem:
Entfernung zum Loch - 3 Kilometer
Die Zeit, für die der Hase das Loch erreichte, beträgt 3 Minuten
Geschwindigkeit ist unbekannt
Wir schreiben diese bekannten Daten mit mathematischen Zeichen
S. - 3 Kilometer
t - 3 Minuten
v -?
Notieren Sie die Formel, um Geschwindigkeit zu finden
v \u003d s: t
Jetzt schreiben wir die Lösung des Problems mit Zahlen auf:
v \u003d 3: 3 \u003d 1 km/min

Wie finde ich eine Entfernung, wenn Zeit und Geschwindigkeit bekannt sind?
Um eine Entfernung zu finden, wenn es Zeit und Geschwindigkeit ist, ist es notwendig, sich mit Geschwindigkeit zu multiplizieren. Ein Beispiel für eine solche Aufgabe:
Der Hase lief mit einer Geschwindigkeit von 1 Kilometer in 1 Minute vom Wolf weg. Er brauchte drei Minuten, um zum Loch zu rennen. Welche Distanz lief der Hase?
Lösung des Problems: Wir schreiben in einen Entwurf, den wir aus den Bedingungen des Problems kennen:
Hase -Geschwindigkeit - 1 Kilometer in 1 Minute
Die Zeit, in der der Hase nach Nora geflohen ist, beträgt 3 Minuten
Entfernung ist unbekannt
Jetzt werden wir dasselbe mit mathematischen Zeichen schreiben:
v - 1 km/min
t - 3 Minuten
S -?
Erinnern Sie sich an die Formel, um die Entfernung zu finden:
S \u003d v ≤ t
Jetzt schreiben wir die Lösung des Problems mit Zahlen auf:
S \u003d 3 ≤ 1 \u003d 3 km

Wie lernt man, komplexere Probleme zu lösen?
Um zu lernen, wie man komplexere Aufgaben löst, müssen Sie verstehen, wie einfache Aufgaben gelöst werden. Denken Sie daran, welche Zeichen die Entfernung, Geschwindigkeit und Zeit angeben. Wenn es nicht möglich ist, sich an die mathematischen Formeln zu erinnern, müssen sie auf ein Blatt Papier ausgeschrieben werden und immer zur Verfügung stehen, während sie Probleme lösen. Lösen Sie mit Ihrem Kind einfache Aufgaben, die beispielsweise während eines Spaziergangs unterwegs erfunden werden können.

Einheiten
Wenn sie Probleme mit Geschwindigkeit, Zeit und Entfernung lösen, machen sie oft einen Fehler, da sie vergessen haben, Einheiten der Messung zu übersetzen.
WICHTIG: Messeinheiten können irgendwelche sein, aber wenn es in einer Aufgabe unterschiedliche Messeinheiten gibt, übersetzen Sie sie gleich. Wenn beispielsweise die Geschwindigkeit in Kilometern pro Minute gemessen wird, muss die Entfernung in Kilometern und in Minuten dargestellt werden.
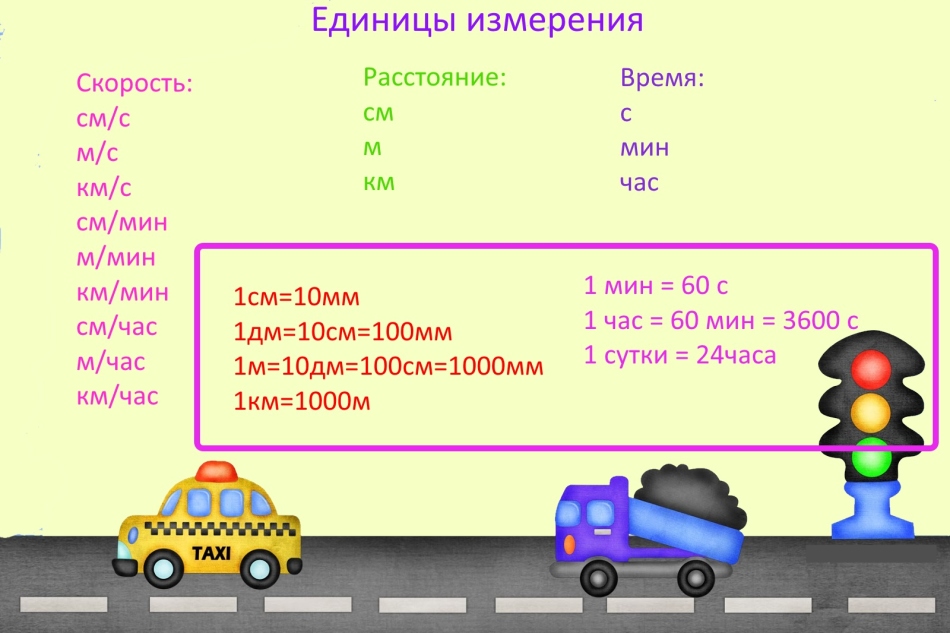
Für neugierig: Das allgemein anerkannte Maßsystem wird jetzt als Metrik bezeichnet, aber dies war nicht immer der Fall, und in den alten Tagen in Russland wurden andere Dimensionseinheiten verwendet.

Die Aufgabe der Boas: Der Elefant und der Affe haben die Länge des BOA -Konstriktors mit Schritten gemessen. Sie bewegten sich aufeinander zu. Die Geschwindigkeit des Affen betrug 60 cm in einer Sekunde und die Elefantengeschwindigkeit beträgt 20 cm in einer Sekunde. Sie verbrachten 5 Sekunden mit der Messung. Was ist die Länge des BOA -Constrictors? (Entscheidung unter dem Bild)

Lösung:
Aus den Bedingungen des Problems bestimmen wir, dass wir die Geschwindigkeit des Affen und des Elefanten und die Zeit kennen, die sie brauchten, um die Länge des Schubs zu messen.
Wir schreiben diese Daten auf:
Affengeschwindigkeit - 60 cm/s
Elefantengeschwindigkeit - 20 cm/s
Zeit - 5 Sekunden
Die Entfernung ist unbekannt
Wir schreiben diese Daten mit mathematischen Zeichen:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 Sekunden
S -?
Lassen Sie uns die Formel für die Entfernung schreiben, wenn Geschwindigkeit und Zeit bekannt sind:
S \u003d v ≤ t
Wir berechnen, wie weit der Affe passiert ist:
S1 \u003d 60 ≤ 5 \u003d 300 cm
Berechnen wir nun, wie viel der Elefant vergangen ist:
S2 \u003d 20 ≤ 5 \u003d 100 cm
Wir fassen die Entfernung zusammen, die der Affe und die Entfernung, die der Elefant bestand:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
Graph der Körpergeschwindigkeit pünktlich: Foto
Der Abstand, der mit unterschiedlichen Geschwindigkeiten überwunden wird, wird in unterschiedlichen Zeiten überwunden. Je größer die Geschwindigkeit, desto weniger Zeit wird es dauern.
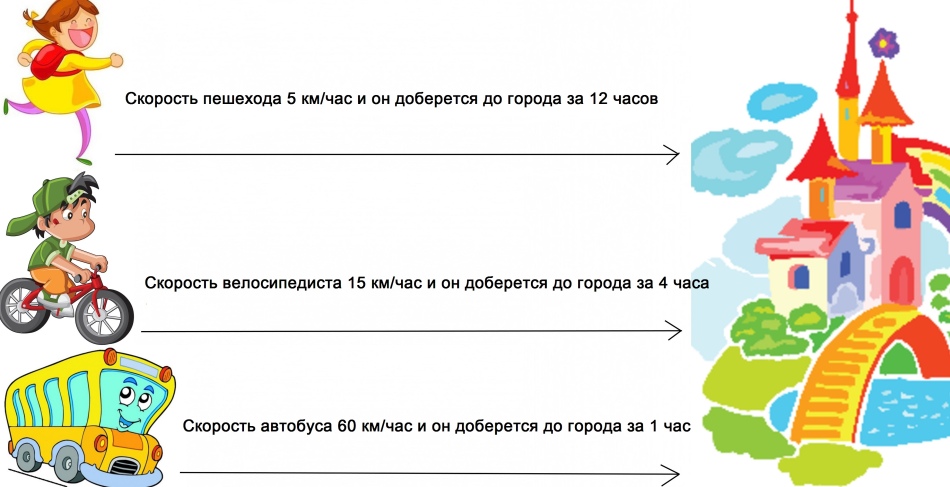
Tabelle 4 Klasse: Geschwindigkeit, Zeit, Entfernung
Die folgende Tabelle zeigt die Daten, für die Sie Probleme haben und sie dann lösen müssen.
| № | Geschwindigkeit (km/Stunde) | Zeit (Stunde) | Entfernung (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Sie können auf Aufgaben für den Tisch selbst phantasieren und selbst erledigen. Im Folgenden finden Sie unsere Optionen für Aufgaben:
- Mama schickte ihrer Großmutter einen roten Hut. Das Mädchen wurde ständig abgelenkt und ging langsam durch den Wald, mit einer Geschwindigkeit von 5 km/h. Sie verbrachte 2 Stunden auf dem Weg. Welche Entfernung ist in dieser Zeit eine rote Kappe bestanden?
- Der Postbote Pechkin nimmt ein Paket mit einer Geschwindigkeit von 12 km/h auf ein Fahrrad. Er weiß, dass die Entfernung zwischen seinem Haus und dem Haus von Onkel Fedor 12 km beträgt. Helfen Sie Pechkin, zu berechnen, wie lange es für die Straße dauern wird?
- Dad Ksyusha kaufte ein Auto und beschloss, seine Familie zum Meer zu bringen. Das Auto fuhr mit einer Geschwindigkeit von 60 km/h und 4 Stunden auf der Straße verbracht. Was ist die Entfernung zwischen dem Haus von Ksyusha und der Seeküste?
- Die Enten versammelten sich im Keil und flogen in die warmen Ränder. Die Vögel winkten mit den Flügeln, die 3 Stunden müde und in dieser Zeit 300 km überwand. Was war die Geschwindigkeit der Vögel?
- Das AN-2-Flugzeug fliegt mit einer Geschwindigkeit von 220 km/h. Er flog aus Moskau und fliegt nach Nizhny Novgorod, der Abstand zwischen diesen beiden Städten 440 km. Wie lange wird das Flugzeug weitergehen?

Die Antworten auf die oben genannten Aufgaben finden Sie in der folgenden Tabelle:
| № | Geschwindigkeit (km/Stunde) | Zeit (Stunde) | Entfernung (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Beispiele für die Lösung von Problemen für Geschwindigkeit, Zeit, Entfernung für Grad 4
Wenn in einer Aufgabe mehrere Bewegungsobjekte vorhanden sind, müssen Sie dem Kind beibringen, die Bewegung dieser Objekte getrennt und nur dann zusammen zu berücksichtigen. Ein Beispiel für eine solche Aufgabe:
Zwei Freunde von Vadik und das Thema beschlossen, einen Spaziergang zu machen, und ließen ihre Häuser aufeinander in Richtung. Vadik fuhr ein Fahrrad und das Thema ging. Vadik ritt mit einer Geschwindigkeit von 10 km/h und das Thema war mit einer Geschwindigkeit von 5 km pro Stunde. Eine Stunde später trafen sie sich. Was ist die Entfernung zwischen Vadiks Häusern und Themen?
Dieses Problem kann unter Verwendung der Formel für die Abhängigkeit der Entfernung von Geschwindigkeit und Zeit gelöst werden.
S \u003d v ≤ t
Die Entfernung, die Vadik mit einem Fahrrad fuhr, entspricht seiner Geschwindigkeit multipliziert mit Reisen.
S \u003d 10 ≤ 1 \u003d 10 Kilometer
Die Entfernung, die das Thema überschritten hat, wird ähnlich betrachtet:
S \u003d v ≤ t
Wir ersetzen die digitalen Werte seiner Geschwindigkeit und Zeit in die Formel
S \u003d 5 ≤ 1 \u003d 5 Kilometer
Die Entfernung, die Vadik fuhr, muss zu der Entfernung hinzugefügt werden, in der das Thema bestand.
10 + 5 \u003d 15 Kilometer
Wie lernt man, wie man komplexe Probleme löst, um zu lösen, was Sie logisch denken müssen?
Um das logische Denken des Kindes zu entwickeln, müssen Sie mit ihm einfach und dann komplexe logische Probleme lösen. Diese Aufgaben können aus mehreren Stufen bestehen. Es ist nur möglich, von einer Stufe in eine andere zu wechseln, wenn der vorherige gelöst wird. Ein Beispiel für eine solche Aufgabe:
Anton fuhr mit einer Geschwindigkeit von 12 km/h mit einem Fahrrad, und Lisa fuhr mit einer Geschwindigkeit von 2 -mal weniger auf einem Roller, und Denis ging mit einer Geschwindigkeit von 2 -mal weniger als die von Lisa. Was ist Denis 'Geschwindigkeit?
Um dieses Problem zu lösen, müssen Sie zuerst die Geschwindigkeit von Lisa und erst nach der Geschwindigkeit dieser Denis herausfinden.

Manchmal gibt es in Lehrbüchern für 4 Klasse schwierige Aufgaben. Ein Beispiel für eine solche Aufgabe:
Zwei Radfahrer verließen verschiedene Städte aufeinander. Einer von ihnen eilte und raste mit einer Geschwindigkeit von 12 km/h, und der zweite fuhr langsam mit einer Geschwindigkeit von 8 km/h. Der Abstand zwischen den Städten, aus denen Radfahrer 60 km verließen. Welche Entfernung wird jeder Radfahrer bestehen, bevor er sich treffen? (Entscheidung unter dem Foto)

Lösung:
- 12+8 \u003d 20 (km/h) ist die Gesamtgeschwindigkeit von zwei Radfahrern oder die Geschwindigkeit, mit der sie sich näherten
- 60 : 20 \u003d 3 (Stunden) - Dies ist die Zeit, durch die sich Radfahrer trafen
- 3 ⋅ 8 \u003d 24 (km) ist der Abstand, den der erste Radfahrer fuhr
- 12 ≤ 3\u003d 36 (km) ist der Abstand, den der zweite Radfahrer fuhr
- Überprüfen Sie: 36+24 \u003d 60 (km) ist die Entfernung, in der zwei Radfahrer reisten.
- Antwort: 24 km, 36 km.
Bieten Sie Kindern in Form eines Spiels an, um solche Probleme zu lösen. Vielleicht werden sie selbst ihre Aufgabe über Freunde, Tiere oder Vögel komponieren wollen.







