Die Formel des Volumens und der Fläche der vollen Oberfläche der Kugel, Sphäre durch den Radius und den Durchmesser des Balls: Wert. Beispiele für die Berechnung der Oberfläche und des Volumens des Balls durch den Radius und den Durchmesser der Kugel: Beschreibung. So finden Sie das Volumen des Balls durch die Oberfläche des Balls: Beispiel

Der Artikel wird für Schulkinder und zukünftige Bewerber nützlich sein, die sich auf die Prüfung vorbereiten.

Formel des Volumes des Balls durch den Radius: Bedeutung

Das Volumen des Balls V wird durch die Formel berechnet (siehe unten), wobei R der Radius des Balls ist, die Zahl „pi“ - π ist eine mathematische Konstante ≈ 3.14.

Diese Formel ist die Basis!

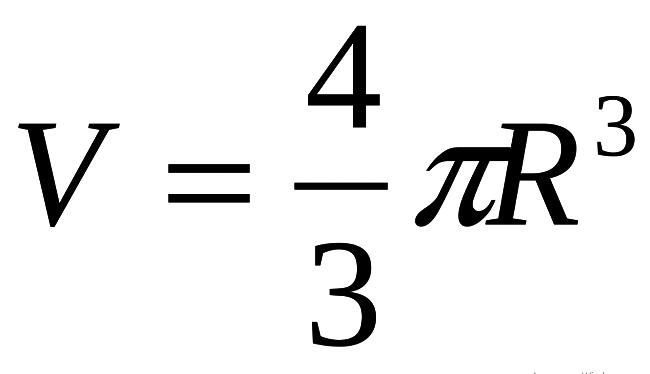
Formel des Volumes des Balls durch den Durchmesser: Wert

1. Verwenden Sie die Basisformel: v \u003d 4/3*π*r³.
2. Der Radius R beträgt einen Durchmesser d oder r \u003d d/2.
3. Daher: v \u003d 4/3*π*r³ → v \u003d (4π/3)*(d/2) ³ → v \u003d (4π/3)*(d³/8) → V \u003d πD.³/6.

Oder

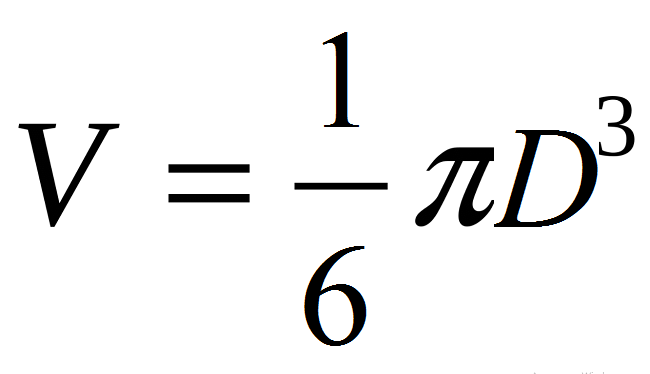
Beispiele für die Berechnung des Balls des Balls, durch den Radius und den Durchmesser des Balls: Beschreibung

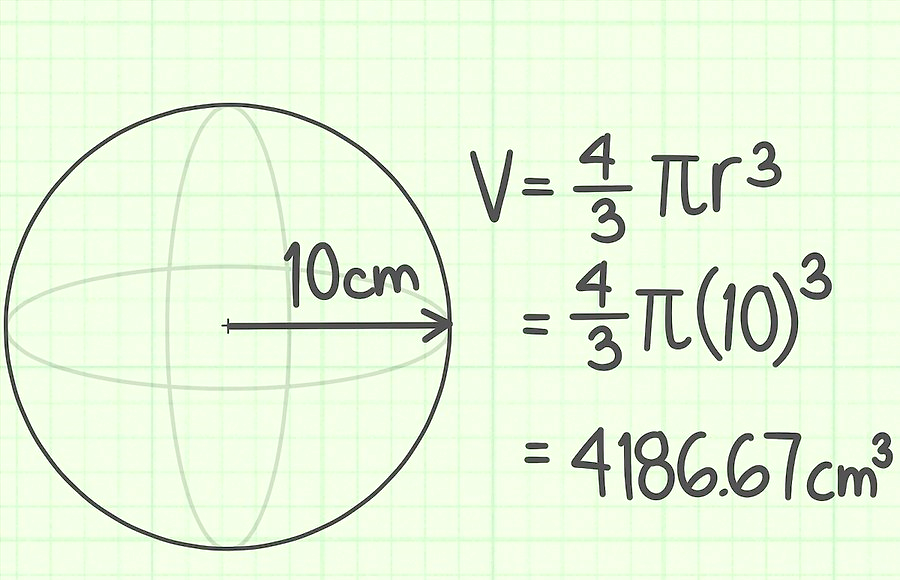
Aufgabe 1.

Der Radius des Balls beträgt 10 cm. Finden Sie sein Volumen.

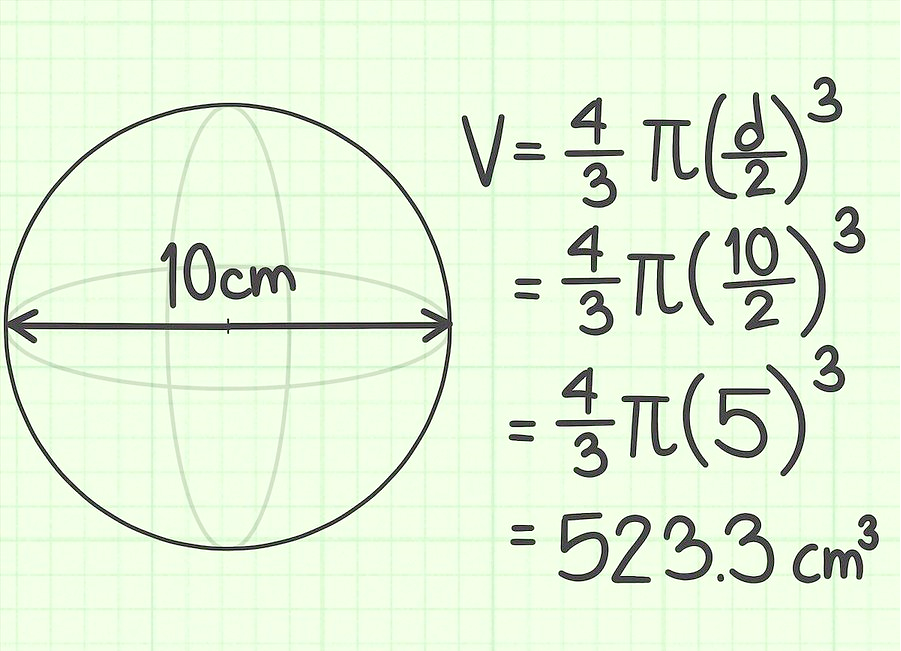
Aufgabe 2.

Der Durchmesser des Balls beträgt 10 cm. Finden Sie sein Volumen.

Aufgabe 3.

Das Verhältnis des Durchmessers des Mondes und des Durchmessers der Erde 1: 4. Wie oft ist das Volumen der Erde größer als das Volumen des Mondes?

Lösung:

Antwort: 64 mal.

Wichtig: Es gibt viele Online -Taschenrechner, mit denen Sie schnell einen bestimmten Wert finden können. Zum Beispiel Service Webmath.

Formel der vollen Oberfläche der Kugel, Kugel durch den Radius: Bedeutung

Die Oberfläche der Kugel/Kugel S wird durch die Formel (siehe unten) berechnet, wobei R der Radius des Balls ist, die Zahl „pi“ - π ist eine mathematische Konstante ≈ 3,14.

Diese Formel ist die Basis!

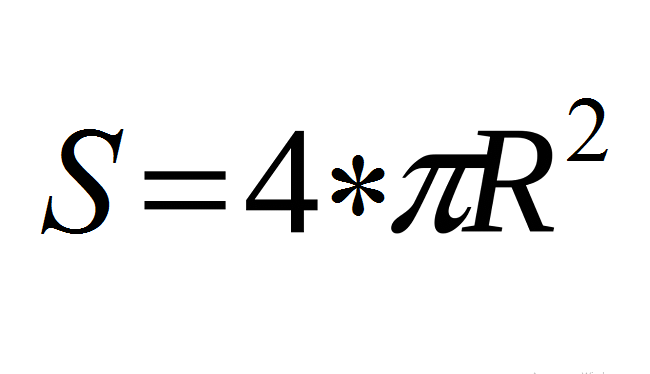
Die Formel der vollen Oberfläche der Kugel, Kugel durch den Durchmesser: Wert

1. Verwenden Sie die Basisformel: s \u003d 4*π*r².
2. Der Radius R beträgt einen Durchmesser d oder r \u003d d/2.
3. Von hier: s \u003d 4*π*r² → s \u003d 4*π*(d/2) ² → s \u003d (4π)*(d²/4) → s \u003d (4πd²)/4 → S \u003d πD.².

Oder

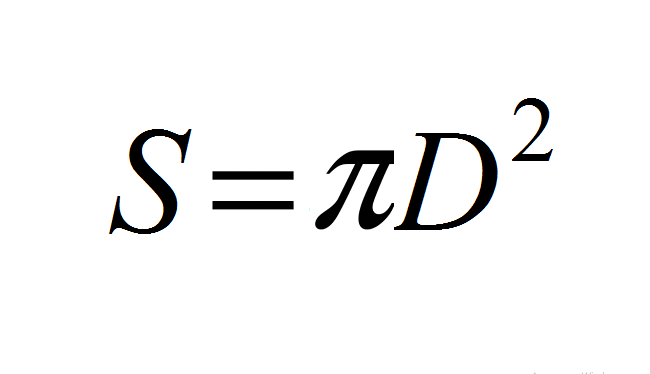
Beispiele für die Berechnung der Oberfläche, der Kugel des Balls, durch den Radius und den Durchmesser der Kugel: Beschreibung

Aufgabe 4.

Aufgabe 5.

Aufgabe 6.

So finden Sie das Volumen des Balls durch die Oberfläche des Balls, Kugel: Ein Beispiel für die Lösung eines Problems

Aufgabe 7.

Aufgabe 8.

Video: Verwenden Sie Mathematik. Das Volumen und die Fläche der Oberfläche der Rotationskörper.