Jak řešit pohyby pro pohyb? Vzorec závislosti mezi rychlostí, časem a vzdáleností. Úkoly a řešení.
Obsah
- Vzorec pro závislost času, rychlosti a vzdálenosti ve 4. ročníku: Jak je rychlost, čas, vzdálenost?
- Jak najít čas, znát rychlost a vzdálenost?
- Jak najít rychlost, pokud je známa čas a vzdálenost?
- Jak najít vzdálenost, pokud je známa čas a rychlost?
- Graf rychlosti těla včas: Fotografie
- Tabulka 4 Třída: Rychlost, čas, vzdálenost
- Příklady řešení problémů rychlosti, času, vzdálenosti pro stupeň 4
- Video: Pohybové úkoly
Vzorec pro závislost času, rychlosti a vzdálenosti ve 4. ročníku: Jak je rychlost, čas, vzdálenost?
Lidé, zvířata nebo auta se mohou pohybovat určitou rychlostí. Po určitou dobu mohou jít určitou cestou. Například: Dnes se můžete dostat do školy za půl hodiny. Jdete určitou rychlostí a překonáte 1000 metrů za 30 minut. Cesta, která je překonána, je v matematice označena dopisem S.. Rychlost je označena dopisem proti. A čas, pro který byla cesta zamítnuta, je označen dopisem t.
- Cesta - S.
- Rychlost- v
- Čas - t
Pokud jste pozdě do školy, můžete jít stejně za 20 minut a zvýšit rychlost. Stejnou cestu tedy lze cestovat v různých časech a různými rychlostmi.
Jak je čas průchodu závislý na rychlosti?
Čím větší je rychlost, tím rychlejší bude vzdálenost. A čím nižší rychlost, tím více času musíte projít cestou.

Jak najít čas, znát rychlost a vzdálenost?
Chcete -li najít čas, který potřebujete projít cestou, musíte znát vzdálenost a rychlost. Pokud je vzdálenost rozdělena do rychlosti, zjistíte čas. Příklad takového úkolu:
Úkol zajíce. Zajíc utekl od vlka rychlostí 1 kilometr za minutu. Běžel ke své díře 3 kilometry. V kolik hodin se zajíc dostal do díry?

Jak je snadné vyřešit problémy pro pohyb, kde musíte najít vzdálenost, čas nebo rychlost?
- Pečlivě si přečtěte úkol a určete, co je známo z podmínek problému.
- Napište tato data do návrhu.
- Také napište, co je neznámé a co je třeba najít
- Použijte vzorec pro úkoly o vzdálenosti, čase a rychlosti
- Zadejte známá data ve vzorci a vyřešte problém
Řešení problému o zajíci a vlku.
- Z podmínek problému určujeme, že známe rychlost a vzdálenost.
- Z podmínek problému také určujeme, že musíme najít čas, který zajíc potřeboval k dosažení díry.

Napíšeme například návrh těchto údajů:
Vzdálenost k díře - 3 kilometry
Rychlost zajíce - 1 kilometr za 1 minutu
Čas není znám
Nyní píšeme stejně jako matematické znaky:
S. - 3 kilometry
V - 1 km/min
t — ?
Vzpomínáme a píšeme vzorec, abychom našli čas v notebooku:
t \u003d S: V
Nyní zapisujeme řešení problému s čísly:
t \u003d 3: 1 \u003d 3 minuty
Jak najít rychlost, pokud je známa čas a vzdálenost?
Aby bylo možné najít rychlost, pokud je známa čas a vzdálenost, musí být vzdálenost na chvíli rozdělena. Příklad takového úkolu:
Zajíc utekl od vlka a běžel k jeho díře 3 kilometry. Tuto vzdálenost překonal za 3 minuty. Jakou rychlostí běžel zajíc?
Řešení problému pohybu:
- V návrhu píšeme, že známe vzdálenost a čas.
- Z podmínek problému určujeme, co je třeba najít rychlost
- Pamatujte na vzorec pro nalezení rychlosti.
Vzorec pro řešení takových problémů jsou uvedeny na obrázku níže.
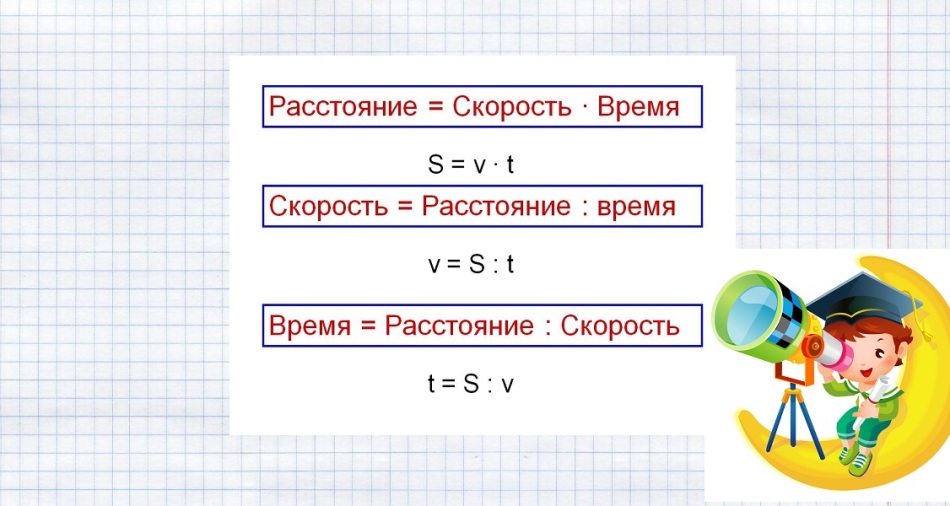
Nahrazujeme známá data a vyřešíme problém:
Vzdálenost k díře - 3 kilometry
Čas, pro který zajíc dorazil do díry, je 3 minuty
Rychlost není známa
Píšeme tato známá data s matematickými znaky
S. - 3 kilometry
t - 3 minuty
v -?
Zaznamenejte vzorec pro nalezení rychlosti
v \u003d s: t
Nyní zapisujeme řešení problému s čísly:
v \u003d 3: 3 \u003d 1 km/min

Jak najít vzdálenost, pokud je známa čas a rychlost?
Pro nalezení vzdálenosti, pokud je známa čas a rychlost, je nutné množit se rychlostí. Příklad takového úkolu:
Zajíc utekl od vlka rychlostí 1 kilometr za 1 minutu. Trvalo mu tři minuty, než se utíkal do díry. Jakou vzdálenost běžel zajíc?
Řešení problému: Píšeme do návrhu, který víme z podmínek problému:
Rychlost zajíce - 1 kilometr za 1 minutu
Čas, kdy zajíc uprchl do Nory, je 3 minuty
Vzdálenost není známa
Nyní napíšeme totéž s matematickými znaky:
v - 1 km/min
t - 3 minuty
S -?
Pamatujte na vzorec pro nalezení vzdálenosti:
S \u003d V ⋅ t
Nyní zapisujeme řešení problému s čísly:
S \u003d 3 ⋅ 1 \u003d 3 km

Jak se naučit řešit složitější problémy?
Chcete -li se naučit, jak řešit složitější úkoly, musíte pochopit, jak jsou řešeny jednoduché úkoly, nezapomeňte, které znaky naznačují vzdálenost, rychlost a čas. Pokud není možné si pamatovat matematické vzorce, musí být zapsány na list papíru a vždy se při řešení problémů měnit. Vyřešete se svým dítětem jednoduché úkoly, které lze vymyslet na cestách, například během procházky.

Jednotky
Když řeší problémy o rychlosti, čase a vzdálenosti, často dělají chybu, protože zapomněli překládat jednotky měření.
DŮLEŽITÉ: Jednotky měření mohou být jakékoli, ale pokud v jednom úkolu existují různé měření, přeložte je stejně. Například, pokud je rychlost měřena v kilometrech za minutu, musí být vzdálenost prezentována v kilometrech a čas v minutách.
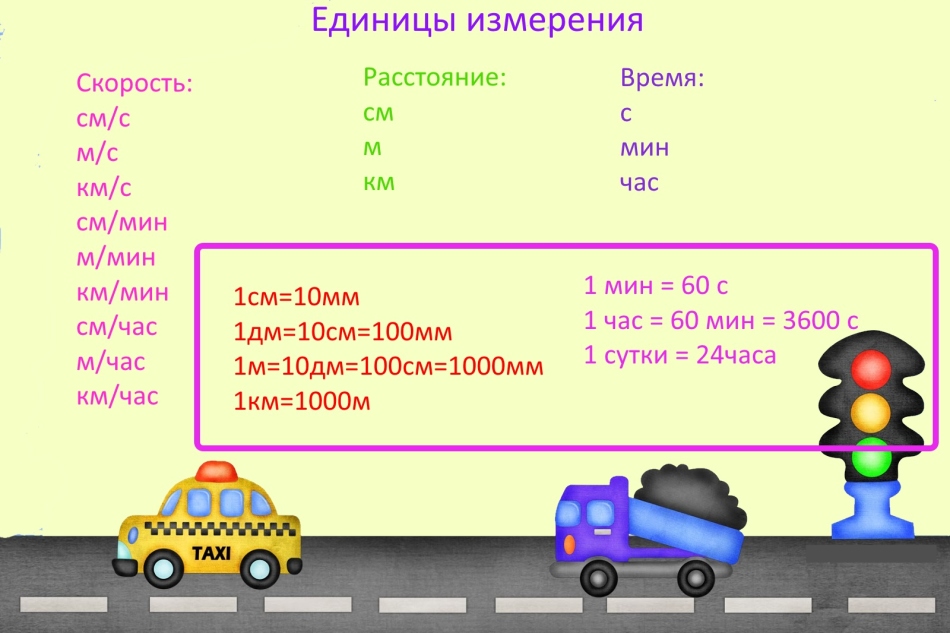
Za zvědavé: Obecně přijímaný systém opatření se nyní nazývá metrika, ale tomu tak nebylo vždy, a za starých časů v Rusku byly použity další jednotky dimenze.

Úkol BOAS: Slon a opice změřili délku konstriktoru BOA kroky. Pohybovali se k sobě. Rychlost opice byla 60 cm za jednu sekundu a rychlost slona je 20 cm za jednu sekundu. Strávili 5 sekund na měření. Jaká je délka konstriktoru BOA? (rozhodnutí pod obrázkem)

Řešení:
Z podmínek problému určujeme, že známe rychlost opice a slona a čas, který potřebovali k měření délky podpory.
Zapíšeme tato data:
Rychlost opice - 60 cm/s
Rychlost slona - 20 cm/s
Čas - 5 sekund
Vzdálenost není známa
Tato data píšeme matematickými značkami:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 sekund
S -?
Pokud je známa rychlost a čas, napište vzorec na dálku:
S \u003d V ⋅ t
Vypočítáme, jak vzdálenost opice prošla:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Nyní si vypočítáme, kolik slon prošel:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Shrnujeme vzdálenost, kterou opice a vzdálenost, kterou slon prošel:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
Graf rychlosti těla včas: Fotografie
Vzdálenost překonána různými rychlostmi je překonána v různých časech. Čím větší je rychlost, tím méně času bude trvat.
Tabulka 4 Třída: Rychlost, čas, vzdálenost
Níže uvedená tabulka ukazuje data, pro která musíte přijít s problémy, a poté je vyřešit.
| № | Rychlost (km/hodina) | Čas (hodina) | Vzdálenost (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Můžete si fantazírovat a přijít s úkoly pro stůl sami. Níže jsou uvedeny naše možnosti úkolů:
- Máma poslala babičce červený klobouk. Dívka byla neustále rozptýlena a procházela lesem pomalu, rychlostí 5 km/h. Strávila 2 hodiny na cestě. Jakou vzdálenost během této doby prošla červená čepice?
- Pošťan Pechkin má zásilku na kole rychlostí 12 km/h. Ví, že vzdálenost mezi jeho domem a domem strýce Fedora je 12 km. Pomozte Pechkin vypočítat, jak dlouho bude trvat na silnici?
- Táta Ksyusha koupil auto a rozhodl se vzít svou rodinu na moře. Auto jezdilo rychlostí 60 km/h a 4 hodiny byly stráveny na silnici. Jaká je vzdálenost mezi domem Ksyusha a mořským pobřežím?
- Kachny se shromáždily v klínu a letěly do teplých okrajů. Ptáci zamávali křídly unaveni po dobu 3 hodin a během této doby překonali 300 km. Jaká byla rychlost ptáků?
- Letadlo AN-2 letí rychlostí 220 km/h. Vyletěl z Moskvy a letěl do Nizhny Novgorod, vzdálenost mezi těmito dvěma městy je 440 km. Jak dlouho půjde letadlo?

Odpovědi na výše uvedené úkoly najdete v níže uvedené tabulce:
| № | Rychlost (km/hodina) | Čas (hodina) | Vzdálenost (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Příklady řešení problémů rychlosti, času, vzdálenosti pro stupeň 4
Pokud v jednom úkolu existuje několik objektů pohybu, musíte dítě naučit, aby zvážilo pohyb těchto objektů samostatně a teprve pak společně. Příklad takového úkolu:
Dva přátelé Vadika a téma se rozhodli projít a nechat své domy k sobě. Vadik jel na kole a téma šlo. Vadik jel rychlostí 10 km/h a téma bylo rychlostí 5 km za hodinu. O hodinu později se setkali. Jaká je vzdálenost mezi vadikovými domy a tématy?
Tento problém lze vyřešit pomocí vzorce pro závislost vzdálenosti na rychlosti a čase.
S \u003d V ⋅ t
Vzdálenost, kterou Vadik jel na kole, se rovná jeho rychlosti vynásobené cestováním.
S \u003d 10 ⋅ 1 \u003d 10 kilometrů
Vzdálenost, kterou téma prošlo, se považuje za podobně:
S \u003d V ⋅ t
Nahrazujeme digitální hodnoty jeho rychlosti a času do vzorce
S \u003d 5 ⋅ 1 \u003d 5 kilometrů
Vzdálenost, kterou Vadik řídil, musí být přidána do vzdálenosti, kterou téma prošlo.
10 + 5 \u003d 15 kilometrů
Jak se naučit, jak řešit složité problémy, pro řešení, které musíte logicky myslet?
Chcete -li rozvíjet logické myšlení dítěte, musíte s ním vyřešit jednoduché a pak složité logické problémy. Tyto úkoly se mohou skládat z několika fází. Je možné přejít z jedné fáze do druhé, pokud je předchozí vyřešena. Příklad takového úkolu:
Anton šel na kolo rychlostí 12 km/h a Lisa jezdila na skútru rychlostí 2krát méně než v Antonu, a Denis šel rychlostí 2krát méně než u Lisy. Jaká je rychlost Denise?
Chcete -li tento problém vyřešit, musíte nejprve zjistit rychlost Lisy a teprve poté, co Denisova rychlost.

Někdy v učebnicích pro 4 třídy jsou obtížné úkoly. Příklad takového úkolu:
Dva cyklisté opustili různá města vůči sobě. Jeden z nich spěchal a závodil rychlostí 12 km/h a druhý jezdil pomalu rychlostí 8 km/h. Vzdálenost mezi městy, ze kterých cyklisté opustili 60 km. Jakou vzdálenost projde každý cyklista, než se setká? (rozhodnutí pod fotografií)

Řešení:
- 12+8 \u003d 20 (km/h) je celková rychlost dvou cyklistů nebo rychlost, s jakou se k sobě přiblížili
- 60 : 20 \u003d 3 (hodiny) - Toto je doba, kdy se cyklisté setkali
- 3 ⋅ 8 \u003d 24 (km) je vzdálenost, kterou řídil první cyklista
- 12 ⋅ 3\u003d 36 (km) je vzdálenost, kterou řídil druhý cyklista
- Zkontrolujte: 36+24 \u003d 60 (km) je vzdálenost, kterou dva cyklisté cestovali.
- Odpověď: 24 km, 36 km.
Nabídněte dětem ve formě hry k vyřešení těchto problémů. Možná oni sami budou chtít si sestavit svůj úkol o přátelství, zvířatech nebo ptácích.







