Vzorec objemu a plochy plného povrchu koule, koule v poloměru a průměr míče: hodnota. Příklady výpočtu povrchové plochy a objemu míče, poloměrem a průměrem míče: popis. Jak najít objem míče přes povrchovou plochu míče: Příklad

Článek bude užitečný pro žáky a budoucí žadatele, kteří se připravují na zkoušku.

Vzorec objemu míče přes poloměr: Význam

Objem míče V se vypočítává podle vzorce (viz níže), kde r je poloměr míče, číslo „pi“ - π je matematická konstanta, ≈ 3,14.

Tento vzorec je základna!

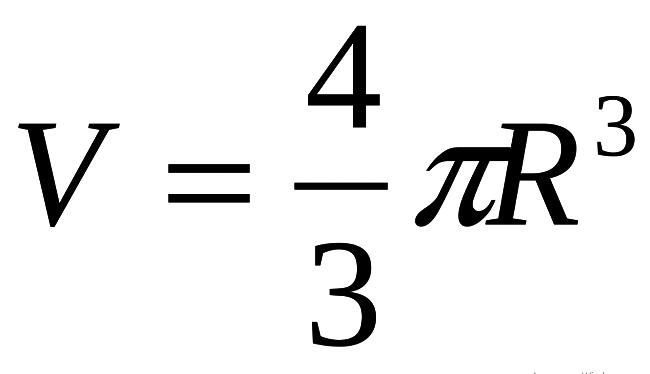
Vzorec objemu míče průměrem: hodnota

1. Použijte základní vzorec: v \u003d 4/3*π*r³.
2. Poloměr r je ½ průměr d nebo r \u003d d/2.
3. Proto: v \u003d 4/3*π*r³ → V \u003d (4π/3)*(d/2) ³ → V \u003d (4π/3)*(d³/8) → V \u003d πD.³/6.

Nebo

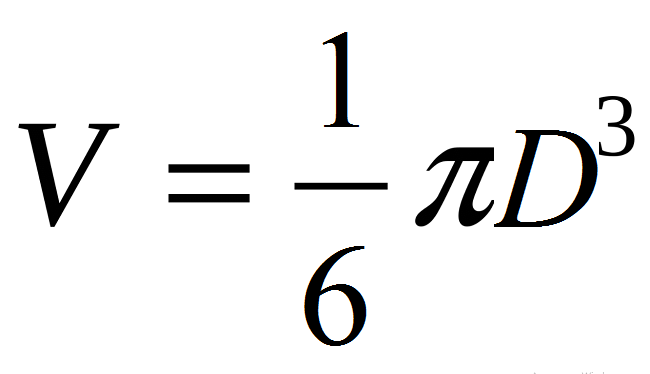
Příklady výpočtu objemu míče přes poloměr a průměr míče: popis

Úkol 1.

Poloměr míče je 10 cm. Najděte jeho objem.

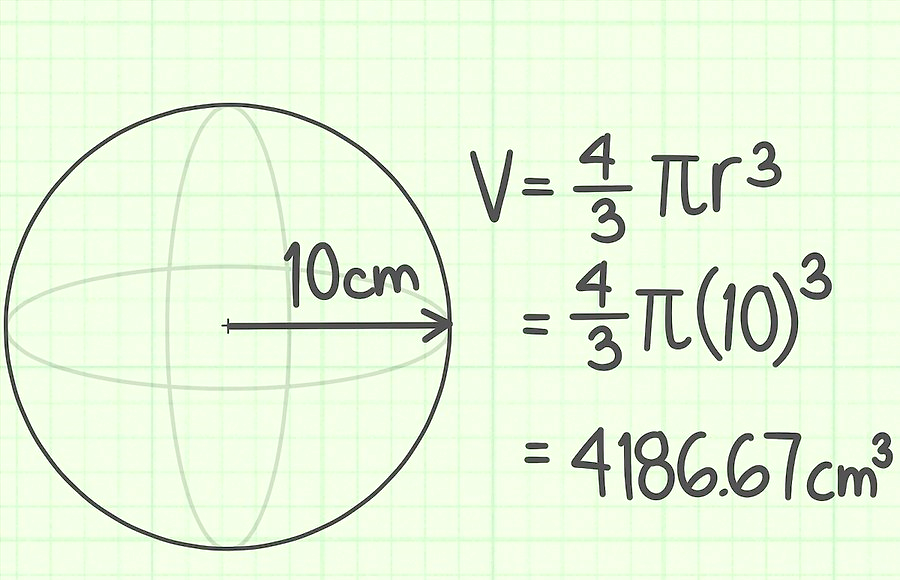
Úkol 2.

Průměr míče je 10 cm. Najděte jeho objem.

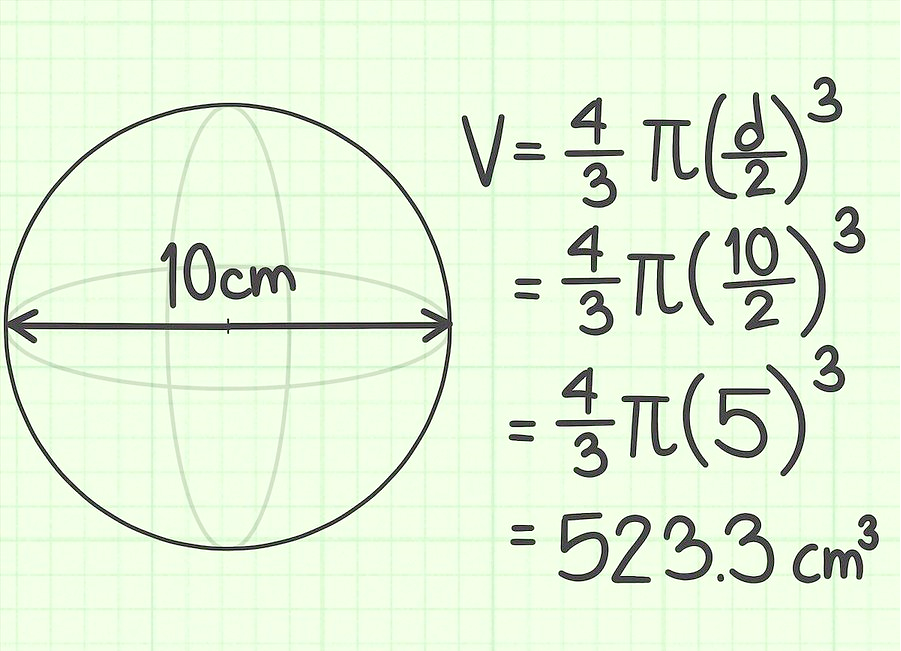
Úkol 3.

Poměr průměru měsíce a průměr Země 1: 4. Kolikrát je objem Země větší než objem měsíce?

Řešení:

Odpověď: 64krát.

Důležité: Existuje mnoho online kalkulaček, které vám umožňují rychle najít danou hodnotu. Například služba Webmath.

Vzorec plného povrchu koule, koule přes poloměr: význam

Povrchová plocha koule/míče S se vypočítá podle vzorce (viz níže), kde r je poloměr míče, číslo „pi“ - π je matematická konstanta, ≈ 3,14.

Tento vzorec je základna!

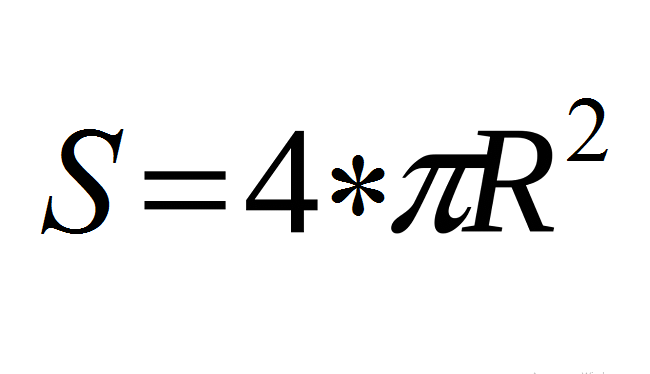
Vzorec plného povrchu koule, koule průměrem: hodnota

1. Použijte základní vzorec: S \u003d 4*π*r².
2. Poloměr r je ½ průměr d nebo r \u003d d/2.
3. Odtud: S \u003d 4*π*r² → S \u003d 4*π*(d/2) ² → S \u003d (4π)*(d²/4) → S \u003d (4πd²)/4 → S \u003d πD.².

Nebo

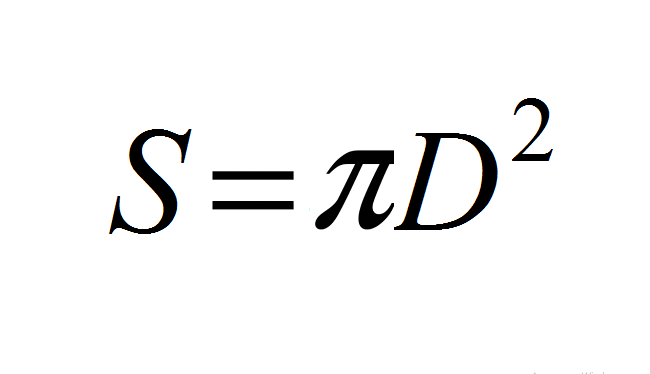
Příklady výpočtu povrchové plochy, koule koule, poloměrem a průměrem míče: popis

Úkol 4.

Úkol 5.

Úkol 6.

Jak najít objem míče přes povrchovou plochu míče, koule: Příklad řešení problému

Úkol 7.

Úkol 8.

Video: Použijte matematiku. Objem a plocha povrchu těl rotace.