Формулата на обема и площта на пълната повърхност на топката, сфера през радиуса и диаметъра на топката: стойност. Примери за изчисляване на повърхността и обема на топката, през радиуса и диаметъра на топката: Описание. Как да намерите обема на топката през повърхността на топката: пример

Статията ще бъде полезна за учениците и бъдещите кандидати, които се подготвят за изпита.

Формула на обема на топката през радиуса: Значение

Обемът на топката V се изчислява по формулата (виж по -долу), където r е радиусът на топката, числото „pi“ - π е математическа константа, ≈ 3.14.

Тази формула е основата!

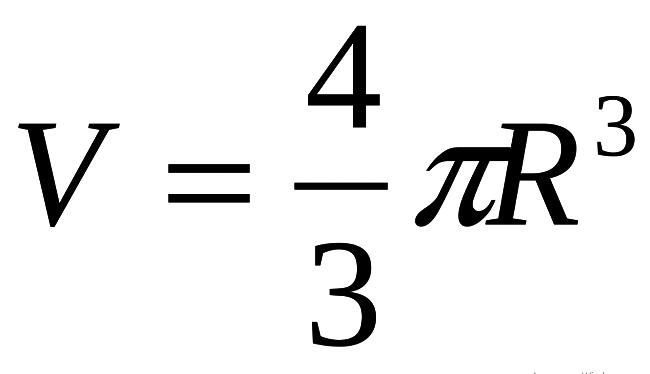
Формула на обема на топката през диаметъра: стойност

1. Използвайте основната формула: V \u003d 4/3*π*r³.
2. Радиус r е ½ диаметър d или r \u003d d/2.
3. Следователно: V \u003d 4/3*π*r³ → V \u003d (4π/3)*(d/2) ³ → V \u003d (4π/3)*(d³/8) → V \u003d πД.³/6.

Или

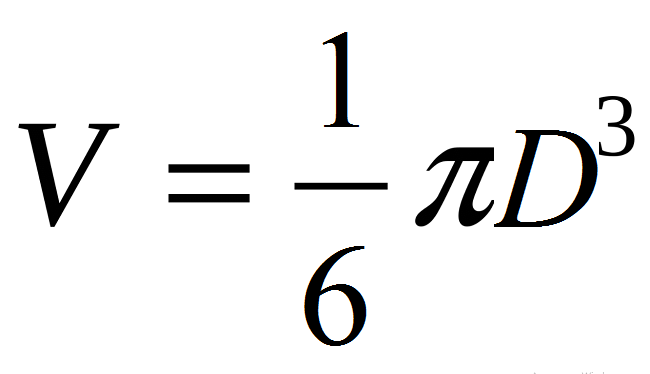
Примери за изчисляване на обема на топката, през радиуса и диаметъра на топката: Описание

Задача 1.

Радиусът на топката е 10 cm. Намерете обема му.

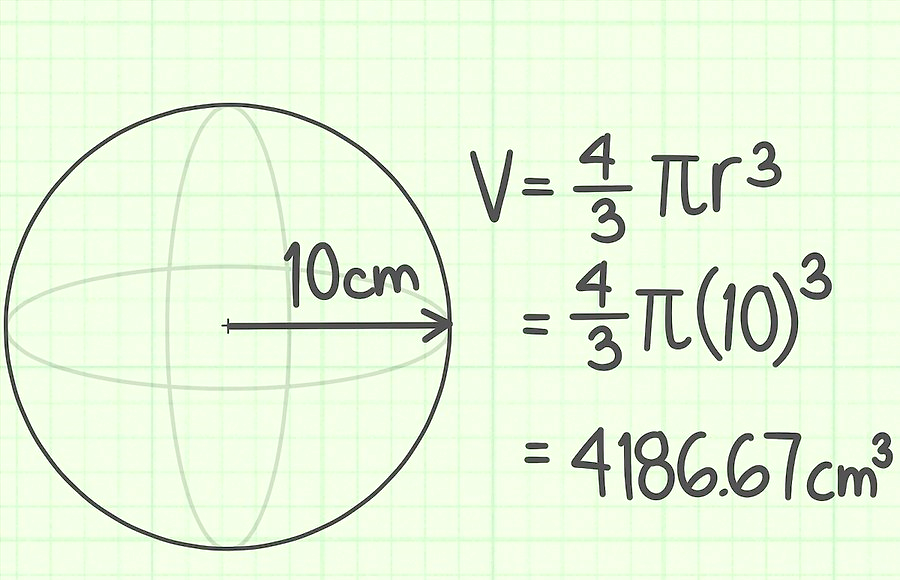
Задача 2.

Диаметърът на топката е 10 cm. Намерете обема му.

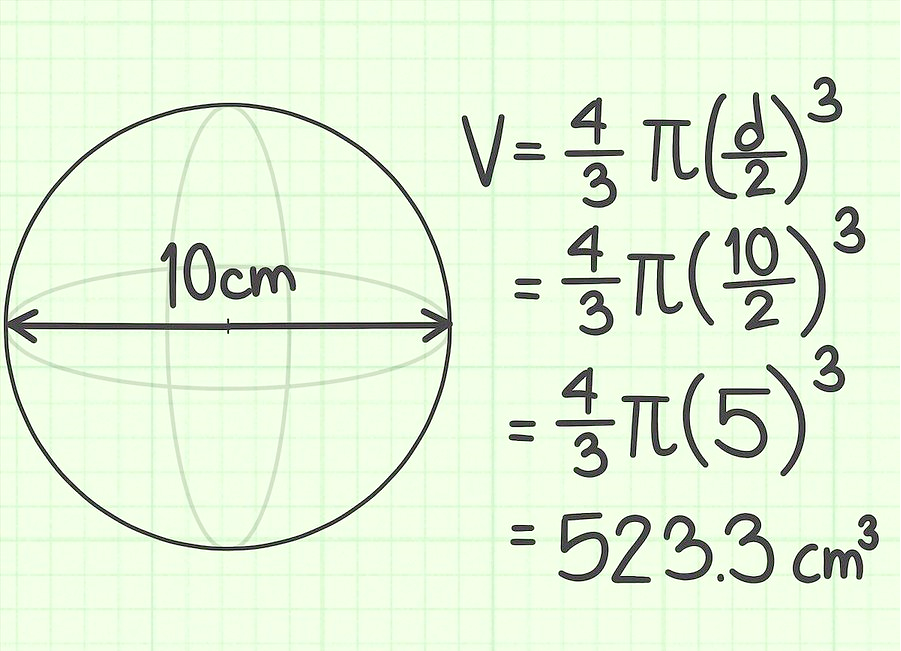
Задача 3.

Съотношението на диаметъра на луната и диаметъра на Земята 1: 4. Колко пъти обемът на земята е по -голям от обема на Луната?

Решение:

Отговор: 64 пъти.

Важно: Има много онлайн калкулатори, които ви позволяват бързо да намерите дадена стойност. Например, обслужване Уебсама.

Формула на пълната повърхност на топката, сфера през радиуса: Значение

Повърхността на сферата/топката s се изчислява по формулата (виж по -долу), където r е радиусът на топката, числото „pi“ - π е математическа константа, ≈ 3.14.

Тази формула е основата!

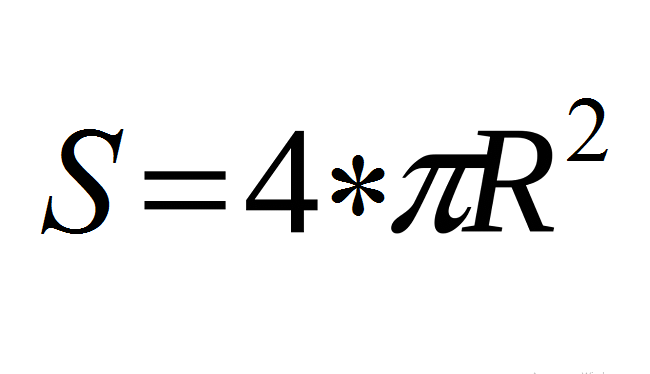
Формулата на цялата повърхност на топката, сфера през диаметъра: стойност

1. Използвайте основната формула: S \u003d 4*π*r².
2. Радиус r е ½ диаметър d или r \u003d d/2.
3. От тук: S \u003d 4*π*r² → S \u003d 4*π*(d/2) ² → S \u003d (4π)*(D²/4) → S \u003d (4πd²)/4 → S \u003d πД.².

Или

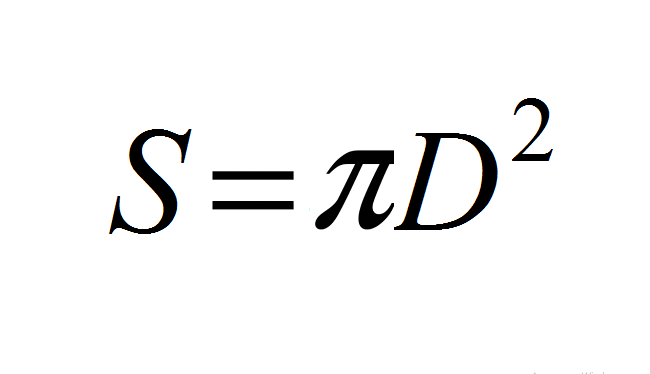
Примери за изчисляване на повърхността, сфера на топката, през радиуса и диаметъра на топката: Описание

Задача 4.

Задача 5.

Задача 6.

Как да намерите обема на топката през повърхността на топката, сфера: Пример за решаване на проблем

Задача 7.

Задача 8.

Видео: Използвайте математика. Обемът и площта на повърхността на телата на въртене.