วิธีแก้ปัญหาการเคลื่อนไหวเพื่อการเคลื่อนไหว? สูตรของการพึ่งพาระหว่างความเร็วเวลาและระยะทาง งานและวิธีแก้ปัญหา
เนื้อหา
- สูตรสำหรับการพึ่งพาเวลาความเร็วและระยะทางเหนือชั้นประถมศึกษาปีที่ 4: ความเร็วเวลาระยะทางเป็นอย่างไร?
- หาเวลารู้ความเร็วและระยะทางได้อย่างไร?
- จะค้นหาความเร็วได้อย่างไรหากทราบเวลาและระยะทาง?
- จะหาระยะห่างได้อย่างไรหากทราบเวลาและความเร็ว?
- กราฟความเร็วร่างกายตรงเวลา: ภาพถ่าย
- ตารางที่ 4 คลาส: ความเร็วเวลาระยะทาง
- ตัวอย่างของการแก้ปัญหาสำหรับความเร็วเวลาระยะทางสำหรับเกรด 4
- วิดีโอ: งานเคลื่อนไหว
สูตรสำหรับการพึ่งพาเวลาความเร็วและระยะทางเหนือชั้นประถมศึกษาปีที่ 4: ความเร็วเวลาระยะทางเป็นอย่างไร?
ผู้คนสัตว์หรือรถยนต์สามารถเคลื่อนที่ได้ด้วยความเร็วที่แน่นอน ในช่วงเวลาหนึ่งพวกเขาสามารถไปตามเส้นทางที่แน่นอน ตัวอย่างเช่น: วันนี้คุณสามารถไปถึงโรงเรียนได้ในครึ่งชั่วโมง คุณไปด้วยความเร็วที่แน่นอนและเอาชนะ 1,000 เมตรใน 30 นาที เส้นทางที่เอาชนะได้ถูกกำหนดไว้ในคณิตศาสตร์โดยจดหมาย พ.. ตัวอักษรระบุความเร็ว v. และเวลาที่เส้นทางถูกปฏิเสธจะถูกระบุโดยจดหมาย t.
- เส้นทาง - พ.
- ความเร็ว- V
- เวลา - t
หากคุณไปโรงเรียนสายคุณสามารถไปในลักษณะเดียวกันใน 20 นาทีเพิ่มความเร็วของคุณ ดังนั้นเส้นทางเดียวกันสามารถเดินทางได้ในช่วงเวลาที่แตกต่างกันและด้วยความเร็วที่แตกต่างกัน
เวลาผ่านไปนั้นขึ้นอยู่กับความเร็วอย่างไร?
ยิ่งความเร็วมากเท่าไหร่ระยะทางก็จะเร็วขึ้นเท่านั้น และยิ่งความเร็วลดลงเท่าไหร่คุณก็ต้องผ่านเส้นทางมากขึ้นเท่านั้น

หาเวลารู้ความเร็วและระยะทางได้อย่างไร?
ในการค้นหาเวลาที่คุณต้องผ่านเส้นทางคุณต้องรู้ระยะทางและความเร็ว หากระยะทางแบ่งออกเป็นความเร็วคุณจะพบเวลา ตัวอย่างของงานดังกล่าว:
ภารกิจของกระต่าย กระต่ายวิ่งออกไปจากหมาป่าด้วยความเร็ว 1 กิโลเมตรต่อนาที เขาวิ่งไปที่หลุม 3 กิโลเมตร กระต่ายไปถึงหลุมกี่โมง?

การแก้ปัญหาการเคลื่อนไหวได้ง่ายแค่ไหนที่คุณต้องหาระยะทางเวลาหรือความเร็ว?
- อ่านงานอย่างระมัดระวังและกำหนดสิ่งที่เป็นที่รู้จักจากเงื่อนไขของปัญหา
- เขียนข้อมูลนี้บนร่าง
- ยังเขียนสิ่งที่ไม่รู้จักและสิ่งที่ต้องพบ
- ใช้สูตรสำหรับงานเกี่ยวกับระยะทางเวลาและความเร็ว
- ป้อนข้อมูลที่รู้จักในสูตรและแก้ปัญหา
วิธีแก้ปัญหาเกี่ยวกับกระต่ายและหมาป่า
- จากเงื่อนไขของปัญหาเราพิจารณาว่าเรารู้ความเร็วและระยะทาง
- นอกจากนี้จากเงื่อนไขของปัญหาเราพิจารณาว่าเราต้องหาเวลาที่กระต่ายที่จำเป็นในการไปถึงหลุม

เราเขียนลงในร่างข้อมูลเหล่านี้ตัวอย่างเช่น:
ระยะทางไปยังหลุม - 3 กิโลเมตร
Hare Speed \u200b\u200b- 1 กิโลเมตรใน 1 นาที
ไม่ทราบเวลา
ตอนนี้เราเขียนเช่นเดียวกับสัญญาณทางคณิตศาสตร์:
พ. - 3 กิโลเมตร
V - 1 กม./นาที
t — ?
เราจำและเขียนสูตรเพื่อค้นหาเวลาในสมุดบันทึก:
t \u003d s: v
ตอนนี้เราเขียนวิธีแก้ปัญหาด้วยตัวเลข:
t \u003d 3: 1 \u003d 3 นาที
จะค้นหาความเร็วได้อย่างไรหากทราบเวลาและระยะทาง?
เพื่อค้นหาความเร็วหากทราบเวลาและระยะทางระยะทางจะต้องแบ่งระยะเวลาสักพัก ตัวอย่างของงานดังกล่าว:
กระต่ายวิ่งออกไปจากหมาป่าและวิ่งไปที่หลุม 3 กิโลเมตร เขาเอาชนะระยะนี้ใน 3 นาที กระต่ายวิ่งด้วยความเร็วเท่าไหร่?
การแก้ปัญหาการเคลื่อนไหว:
- ในร่างเราเขียนว่าเรารู้ระยะทางและเวลา
- จากเงื่อนไขของปัญหาเรากำหนดสิ่งที่ต้องพบความเร็ว
- จำสูตรสำหรับการค้นหาความเร็ว
สูตรสำหรับการแก้ปัญหาดังกล่าวจะแสดงในภาพด้านล่าง
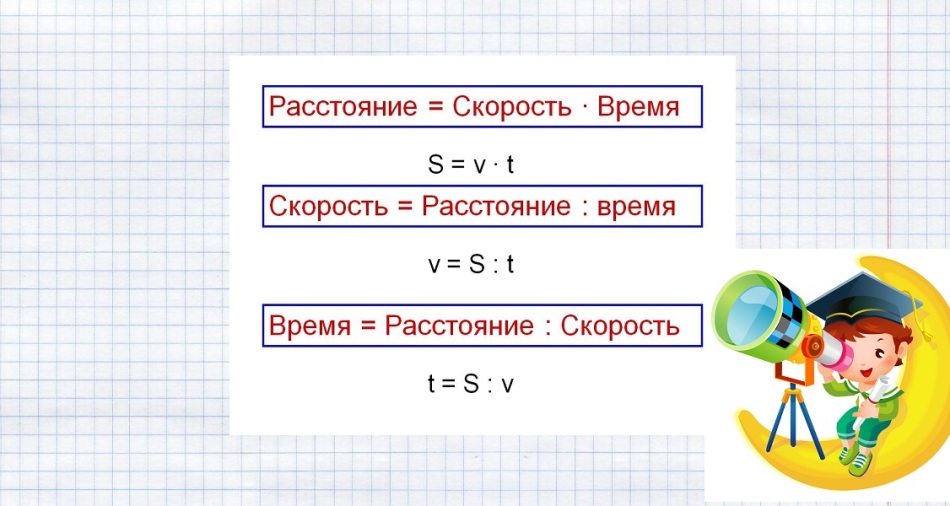
เราแทนที่ข้อมูลที่รู้จักและแก้ปัญหา:
ระยะทางไปยังหลุม - 3 กิโลเมตร
เวลาที่กระต่ายมาถึงหลุมคือ 3 นาที
ไม่ทราบความเร็ว
เราเขียนข้อมูลที่รู้จักเหล่านี้ด้วยสัญญาณทางคณิตศาสตร์
พ. - 3 กิโลเมตร
t - 3 นาที
v -?
บันทึกสูตรเพื่อค้นหาความเร็ว
v \u003d S: T
ตอนนี้เราเขียนวิธีแก้ปัญหาด้วยตัวเลข:
v \u003d 3: 3 \u003d 1 km/นาที

จะหาระยะห่างได้อย่างไรหากทราบเวลาและความเร็ว?
ในการค้นหาระยะทางหากเป็นเวลาและความเร็วที่รู้จักจำเป็นต้องทวีคูณด้วยความเร็ว ตัวอย่างของงานดังกล่าว:
กระต่ายวิ่งออกไปจากหมาป่าด้วยความเร็ว 1 กิโลเมตรใน 1 นาที เขาใช้เวลาสามนาทีในการวิ่งไปที่หลุม กระต่ายวิ่งระยะไกล?
วิธีแก้ปัญหา: เราเขียนถึงร่างที่เรารู้จากเงื่อนไขของปัญหา:
Hare Speed \u200b\u200b- 1 กิโลเมตรใน 1 นาที
เวลาที่กระต่ายหนีไปนอร่าคือ 3 นาที
ไม่ทราบระยะทาง
ตอนนี้เราจะเขียนสิ่งเดียวกันด้วยสัญญาณทางคณิตศาสตร์:
v - 1 กม./นาที
t - 3 นาที
s -?
จำสูตรสำหรับการค้นหาระยะทาง:
S \u003d V ⋅ T
ตอนนี้เราเขียนวิธีแก้ปัญหาด้วยตัวเลข:
S \u003d 3 ⋅ 1 \u003d 3 กม.

วิธีการเรียนรู้ที่จะแก้ปัญหาที่ซับซ้อนมากขึ้น?
หากต้องการเรียนรู้วิธีแก้ปัญหางานที่ซับซ้อนมากขึ้นคุณต้องเข้าใจว่างานง่าย ๆ ได้รับการแก้ไขอย่างไรโปรดจำไว้ว่าสัญญาณใดที่บ่งบอกถึงระยะทางความเร็วและเวลา หากเป็นไปไม่ได้ที่จะจดจำสูตรทางคณิตศาสตร์พวกเขาจะต้องเขียนลงบนแผ่นกระดาษและเก็บไว้ในมือเสมอในขณะที่แก้ปัญหา แก้ปัญหากับงานง่ายๆของลูกที่สามารถคิดค้นได้ในระหว่างการเดินทางเช่นระหว่างการเดิน

หน่วย
เมื่อพวกเขาแก้ปัญหาเกี่ยวกับความเร็วเวลาและระยะทางพวกเขามักจะทำผิดเนื่องจากความจริงที่ว่าพวกเขาลืมที่จะแปลหน่วยการวัด
สิ่งสำคัญ: หน่วยการวัดสามารถทำได้ แต่หากมีหน่วยการวัดที่แตกต่างกันในงานเดียวให้แปลเหมือนกัน ตัวอย่างเช่นหากวัดความเร็วเป็นกิโลเมตรต่อนาทีระยะทางจะต้องแสดงเป็นกิโลเมตรและเวลาในไม่กี่นาที
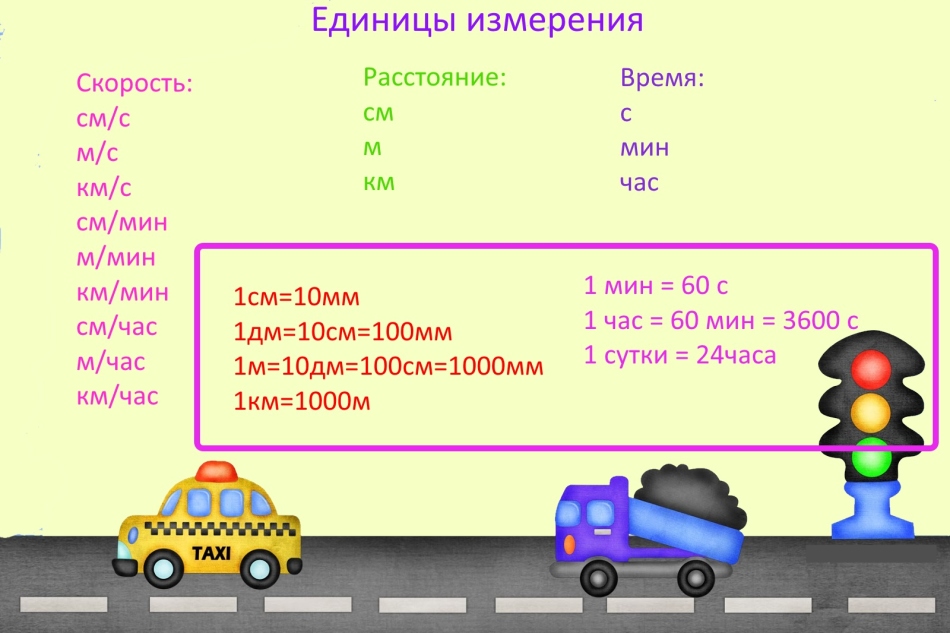
เพื่อความอยากรู้อยากเห็น: ระบบมาตรการที่ได้รับการยอมรับโดยทั่วไปเรียกว่าตัวชี้วัดในขณะนี้ แต่นี่ไม่ใช่กรณีเสมอไปและในสมัยก่อนในมิติอื่น ๆ ของรุสถูกนำมาใช้

ภารกิจของงูเหลือม: ช้างและลิงวัดความยาวของงูเหลือมบีบอัดด้วยขั้นตอน พวกเขาย้ายเข้าหากัน ความเร็วของลิงคือ 60 ซม. ในหนึ่งวินาทีและความเร็วช้างคือ 20 ซม. ในหนึ่งวินาที พวกเขาใช้เวลา 5 วินาทีในการวัด ความยาวของ BOA constrictor คืออะไร? (การตัดสินใจภายใต้ภาพ)

วิธีการแก้:
จากเงื่อนไขของปัญหาเราพิจารณาว่าเรารู้ความเร็วของลิงและช้างและเวลาที่พวกเขาต้องการในการวัดความยาวของการเพิ่ม
เราเขียนข้อมูลเหล่านี้:
ความเร็วลิง - 60 ซม./วินาที
ความเร็วช้าง - 20 ซม./วินาที
เวลา - 5 วินาที
ไม่ทราบระยะทาง
เราเขียนข้อมูลนี้ด้วยสัญญาณทางคณิตศาสตร์:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 วินาที
s -?
ให้เราเขียนสูตรสำหรับระยะทางหากเป็นที่รู้จักความเร็วและเวลา:
S \u003d V ⋅ T
เราคำนวณระยะทางของลิงผ่านไปแล้ว:
S1 \u003d 60 ⋅ 5 \u003d 300 ซม.
ตอนนี้เรามาคำนวณว่าช้างผ่านไปมากน้อยแค่ไหน:
S2 \u003d 20 ⋅ 5 \u003d 100 ซม.
เราสรุประยะทางที่ลิงและระยะทางที่ช้างผ่านไป:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
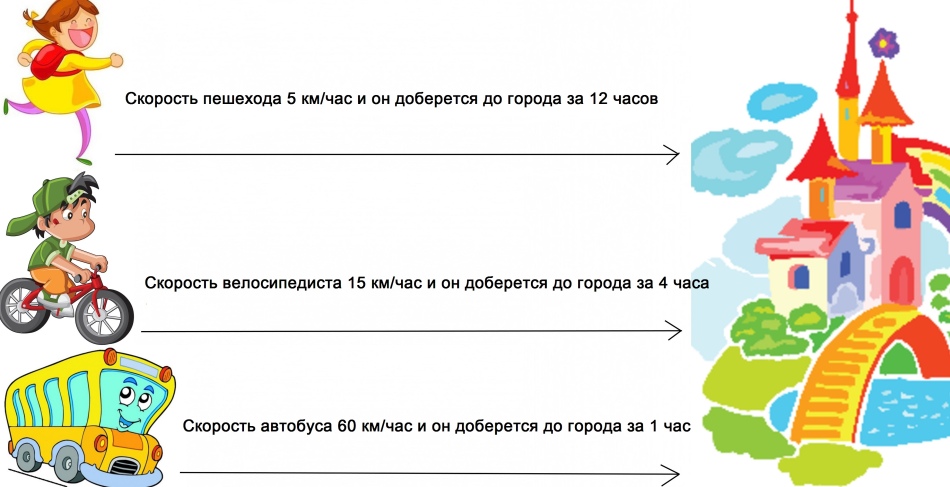
กราฟความเร็วร่างกายตรงเวลา: ภาพถ่าย
ระยะทางที่เอาชนะด้วยความเร็วที่แตกต่างกันจะเอาชนะในเวลาที่ต่างกัน ยิ่งความเร็วมากขึ้นเท่าไหร่เวลาก็น้อยลงเท่านั้น
ตารางที่ 4 คลาส: ความเร็วเวลาระยะทาง
ตารางด้านล่างแสดงข้อมูลที่คุณต้องมีปัญหาแล้วแก้ปัญหา
| № | ความเร็ว (km/ชั่วโมง) | เวลา (ชั่วโมง) | ระยะทาง (กม.) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
คุณสามารถจินตนาการและหางานให้กับโต๊ะด้วยตัวเอง ด้านล่างนี้เป็นตัวเลือกของเราสำหรับงาน:
- แม่ส่งหมวกสีแดงให้คุณยายของเธอ หญิงสาวถูกฟุ้งซ่านอย่างต่อเนื่องและเดินผ่านป่าอย่างช้าๆด้วยความเร็ว 5 กม./ชม. เธอใช้เวลา 2 ชั่วโมงบนเส้นทาง ช่วงเวลาใดที่มีหมวกสีแดงผ่านไปในช่วงเวลานี้?
- Postman Pechkin ใช้พัสดุบนจักรยานด้วยความเร็ว 12 กม./ชม. เขารู้ว่าระยะห่างระหว่างบ้านของเขากับบ้านของลุงเฟเดอร์คือ 12 กม. Help Pechkin คำนวณว่าจะใช้เวลานานแค่ไหนสำหรับถนน?
- พ่อ Ksyusha ซื้อรถและตัดสินใจพาครอบครัวไปทะเล รถขับด้วยความเร็ว 60 กม./ชม. และใช้เวลาบนท้องถนน ระยะห่างระหว่างบ้านของ Ksyusha และชายฝั่งทะเลคืออะไร?
- เป็ดรวมตัวกันในลิ่มและบินเข้าไปในขอบอันอบอุ่น นกโบกปีกของพวกเขาเหนื่อยเป็นเวลา 3 ชั่วโมงและเอาชนะ 300 กม. ในช่วงเวลานี้ ความเร็วของนกคืออะไร?
- เครื่องบิน AN-2 บินด้วยความเร็ว 220 กม./ชม. เขาบินออกจากมอสโกและบินไปยัง Nizhny Novgorod ระยะห่างระหว่างสองเมืองนี้คือ 440 กม. เครื่องบินจะไปได้นานแค่ไหน?

คำตอบของงานด้านบนสามารถพบได้ในตารางด้านล่าง:
| № | ความเร็ว (km/ชั่วโมง) | เวลา (ชั่วโมง) | ระยะทาง (กม.) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
ตัวอย่างของการแก้ปัญหาสำหรับความเร็วเวลาระยะทางสำหรับเกรด 4
หากมีวัตถุหลายอย่างในการเคลื่อนไหวในงานเดียวคุณต้องสอนเด็กให้พิจารณาการเคลื่อนไหวของวัตถุเหล่านี้แยกกันและจากนั้นก็รวมกันเท่านั้น ตัวอย่างของงานดังกล่าว:
เพื่อนสองคนของวาดิคและหัวข้อตัดสินใจที่จะเดินเล่นและออกจากบ้านของพวกเขาต่อกัน วาดิคขี่จักรยานและหัวข้อกำลังเดินอยู่ Vadik ขี่ด้วยความเร็ว 10 กม./ชม. และหัวข้ออยู่ที่ความเร็ว 5 กม. ต่อชั่วโมง หนึ่งชั่วโมงต่อมาพวกเขาพบกัน ระยะห่างระหว่างบ้านและหัวข้อของวาดิคคืออะไร?
ปัญหานี้สามารถแก้ไขได้โดยใช้สูตรสำหรับการพึ่งพาระยะทางด้วยความเร็วและเวลา
S \u003d V ⋅ T
ระยะทางที่วาดิคขับรถจักรยานจะเท่ากับความเร็วของเขาคูณด้วยการเดินทาง
S \u003d 10 ⋅ 1 \u003d 10 กิโลเมตร
ระยะทางที่หัวข้อผ่านไปนั้นถือว่าเป็นเช่นเดียวกัน:
S \u003d V ⋅ T
เราแทนที่ค่าดิจิตอลของความเร็วและเวลาเป็นสูตร
S \u003d 5 ⋅ 1 \u003d 5 กิโลเมตร
ระยะทางที่วาดิคขับจะต้องเพิ่มในระยะทางที่หัวข้อผ่านไป
10 + 5 \u003d 15 กิโลเมตร
วิธีการเรียนรู้วิธีแก้ปัญหาที่ซับซ้อนสำหรับการแก้ปัญหาที่คุณต้องคิดอย่างมีเหตุผล?
ในการพัฒนาความคิดเชิงตรรกะของเด็กคุณต้องแก้ไขกับเขาง่ายๆและปัญหาเชิงตรรกะที่ซับซ้อน งานเหล่านี้อาจประกอบด้วยหลายขั้นตอน เป็นไปได้ที่จะย้ายจากขั้นตอนหนึ่งไปอีกขั้นหนึ่งหากก่อนหน้านี้ได้รับการแก้ไข ตัวอย่างของงานดังกล่าว:
แอนตันไปขี่จักรยานด้วยความเร็ว 12 กม./ชม. และลิซ่าขี่สกูตเตอร์ด้วยความเร็วน้อยกว่าแอนตัน 2 เท่าและเดนิสเดินด้วยความเร็วน้อยกว่าลิซ่า 2 เท่า ความเร็วของเดนิสคืออะไร?
ในการแก้ปัญหานี้คุณต้องค้นหาความเร็วของลิซ่าก่อนและหลังจากความเร็วของเดนิส

บางครั้งในตำราเรียนสำหรับ 4 เกรดมีงานที่ยาก ตัวอย่างของงานดังกล่าว:
นักปั่นจักรยานสองคนออกจากเมืองต่าง ๆ ซึ่งกันและกัน หนึ่งในนั้นรีบเร่งและวิ่งด้วยความเร็ว 12 กม./ชม. และขี่ครั้งที่สองอย่างช้าๆด้วยความเร็ว 8 กม./ชม. ระยะห่างระหว่างเมืองที่นักปั่นจักรยานเหลือ 60 กม. นักปั่นจักรยานแต่ละคนจะผ่านไประยะใดก่อนที่จะพบกัน? (การตัดสินใจภายใต้ภาพถ่าย)

วิธีการแก้:
- 12+8 \u003d 20 (km/h) คือความเร็วรวมของนักปั่นจักรยานสองคนหรือความเร็วที่พวกเขาเข้าหากัน
- 60 : 20 \u003d 3 (ชั่วโมง) - นี่คือเวลาที่นักปั่นจักรยานพบกัน
- 3 ⋅ 8 \u003d 24 (km) เป็นระยะทางที่นักปั่นจักรยานคนแรกขับรถ
- 12 ⋅ 3\u003d 36 (km) เป็นระยะทางที่นักปั่นจักรยานคนที่สองขับรถ
- ตรวจสอบ: 36+24 \u003d 60 (km) เป็นระยะทางที่นักปั่นจักรยานสองคนเดินทาง
- คำตอบ: 24 กม., 36 กม.
เสนอเด็ก ๆ ในรูปแบบของเกมเพื่อแก้ปัญหาดังกล่าว บางทีพวกเขาอาจต้องการแต่งภารกิจเกี่ยวกับเพื่อนสัตว์หรือนก







