Jak znaleźć kwadratowy obszar, jeśli obwód jest znany, przekątna? Jak znaleźć kwadrat kwadratu wpisany w kółko i opisany w pobliżu koła: wzór, przykłady problemów rozwiązywania. Jak znaleźć stronę i przekątną kwadratu, jeśli jego obszar jest znany?

Przeczytaj artykuł, aby dowiedzieć się, jak znaleźć obszar kwadratowy na różne sposoby.

Kwadrat jest równobocznym prostokątem. Ten właściwy i płaski czworokąt ma równość ze wszystkich stron, narożników i przekąt. Ze względu na fakt, że istnieje taka równość, formuła obliczania obszaru i innych cech jest nieznacznie zmodyfikowana w porównaniu z innymi postaciami matematycznymi. Ale to nie sprawia, że \u200b\u200bzadania jest zbyt skomplikowane. Przeanalizujmy wszystkie formuły i rozwiązania problemów w tym artykule.

Jak znaleźć bok kwadratu, znając jego obszar?

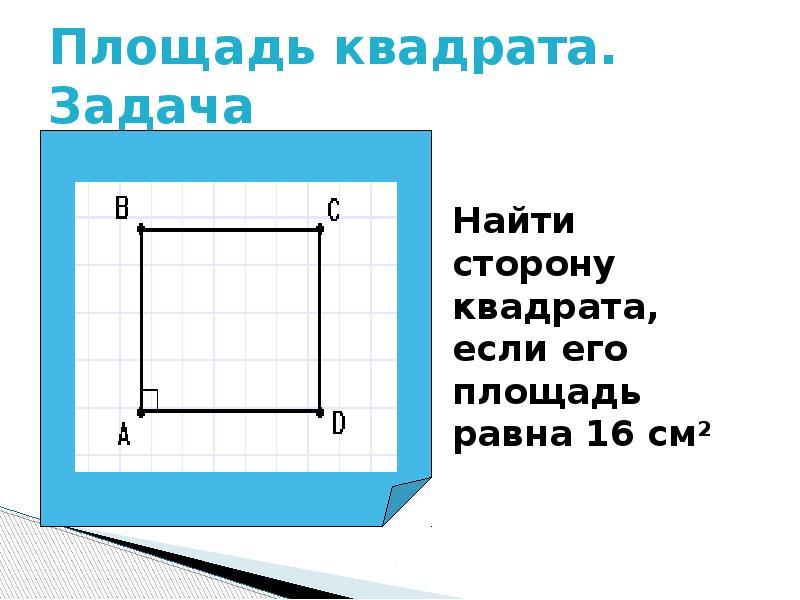
Kwadrat S. Kwadraty bezpośrednie i kwadratowe są obliczane według wzoru: A Pomnożyć przez b.. Ale ponieważ kwadrat ma całkowitą równość stron, jego obszar będzie równy: S \u003d (a) w drugim stopniu.  Jak dowiedzieć się wielkości boku kwadratu, znając jego obszar?

• Jeśli obszar kwadratu jest znany, znajdziemy stronę, obliczając obszar spod korzenia kwadratowego.
• Na przykład powierzchnia kwadratu wynosi 49, a potem jaka jest strona?
• 49 \u003d (a) w drugim stopniu. Rozwiązanie: a \u003d korzeń 49 \u003d 7. Odpowiedź: 7.

Jeśli chcesz znaleźć bok kwadratowego kwadratu, którego obszar jest zbyt długi, użyj kalkulatora. Najpierw wybierz liczbę obszaru, a następnie naciśnij znak główny na klawiaturze kalkulatora. Powstała liczba będzie odpowiedzią.

Jak znaleźć kwadratową przekątną, jeśli jego obszar jest znany?

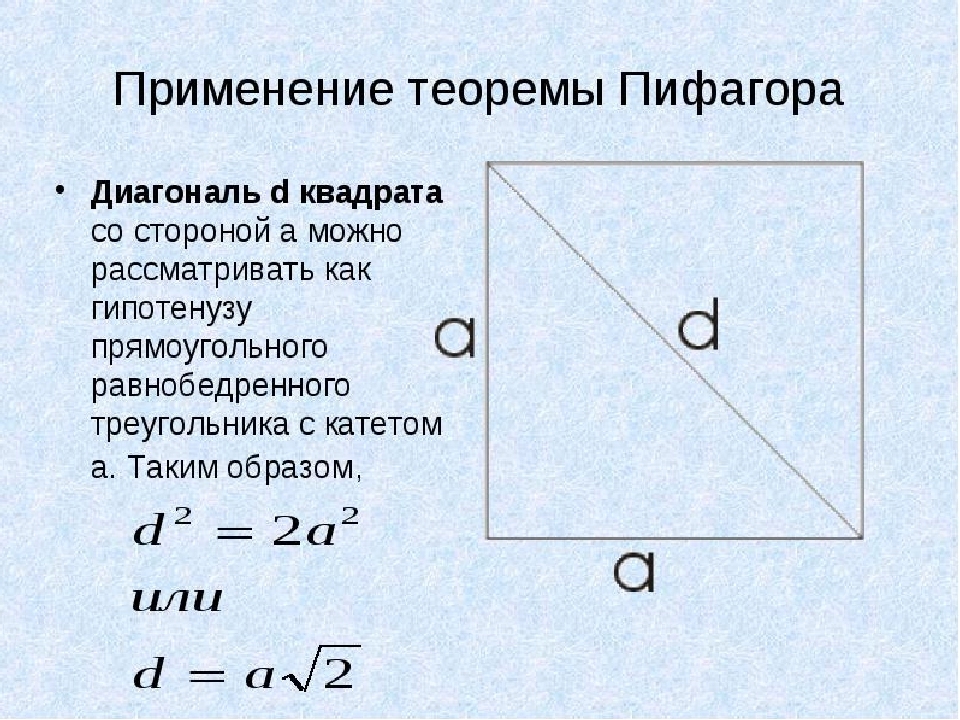
W tym przykładzie użyjemy twierdzenia Pitagorasa. Na kwadracie wszystkie strony są równe, a przekątna d. Rozważymy za hipotencję prostokątnego trójkąta izoscelesowego z nogą a. Teraz znajdujemy kwadratową przekątną, jeśli jego obszar jest znany:

• Aby nie pomalować całego twierdzenia Pitagorean, zdecydujemy o drugiej opcji: d \u003d Aising, gdzie A jest stroną kwadratu.
• Znamy więc kwadrat kwadratu, na przykład jest on równy 64. Tak więc jedna strona a \u003d √64 \u003d 8.
• Okazało się D \u003d 8√2. Korzeń 2 nie okazuje się liczbą całkowitą, więc w odpowiedzi możesz napisać w ten sposób: d \u003d 8√2. Ale jeśli chcesz obliczyć wartość, użyj kalkulatora: √2 \u003d 1,41421356237 i pomnóż przez 8, okazuje się 11, 3137084.

Ważny: Zazwyczaj w matematyce brak liczb z dużą liczbą liczb po AIM pozostanie w odpowiedzi. Konieczne jest zaokrąglanie lub opuszczenie korzenia. Dlatego odpowiedź na przekątkę brzmi, jeśli obszar wynosi 64 w następujący sposób: d \u003d 8√2.

Jak znaleźć kwadratowy obszar przez przekątną?

Formuła znalezienia powierzchni kwadratowej przez przekątkę jest prosta:

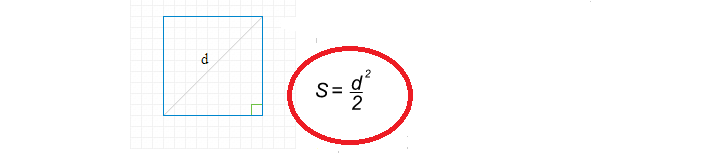
Teraz napiszmy rozwiązanie, aby znaleźć powierzchnię kwadratową przez przekątną:

• Diagonal D \u003d 8.
• 8 na placu ma 64.
• 64 Podziel przez 2 równe 32.
• Obszar kwadratu wynosi 32.

Rada: To zadanie ma inne rozwiązanie poprzez twierdzenie Pitagorasa, ale jest bardziej skomplikowane. Dlatego użyj badanego rozwiązania.

Jak znaleźć kwadratowy obszar, znając jego obwód?

Obwód kwadratu P. - To jest suma wszystkich stron. Aby znaleźć jego obszar, znając jego obwód, musisz najpierw obliczyć bok kwadratowego kwadratu. Rozwiązanie:

• Załóżmy, że obwód wynosi 24. Podziel 24 na 4 strony, okazuje się 6 - to jedna strona.
• Teraz używamy formuły do \u200b\u200bznalezienia obszaru, wiedząc, jaka jest strona kwadratowego kwadratu, jest równa: S \u003d a na kwadratach, s \u003d 6 na kwadratie \u003d 36.
• Odpowiedź: 36

Jak widać, znając obwód placu, po prostu znajdź jego obszar.

Jak znaleźć obszar kwadratu wpisanego w okręgu o danym promieniu?

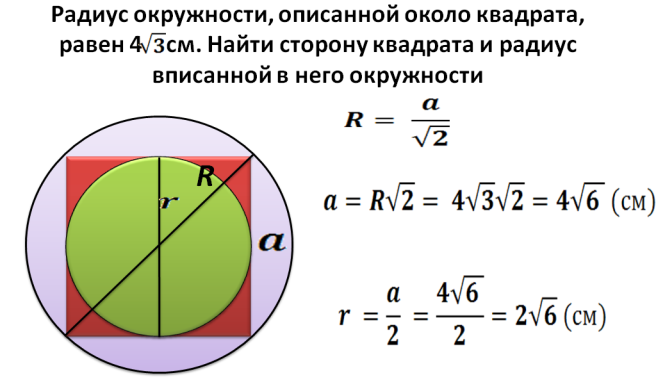
Promień R - Jest to połowa przekątna kwadratu wpisanego w koło. Teraz możemy znaleźć przekątną według wzoru: d \u003d 2*r. Następnie znajdujemy kwadrat kwadratu wpisany w okręgu o danym promieniu:

• Pigonalna jest równa 2 pomnożona przez promień. Na przykład promień wynosi 5, wówczas przekątna jest równa 2*5=10.
• Opisano powyżej, jak znaleźć kwadrat kwadratu, jeśli znany jest przekątna: S \u003d przekątna w kwadratowym podziale przez 2. S \u003d 10*10 i podziel przez 2 \u003d 50.
• Odpowiedź - 50.

To zadanie jest nieco bardziej skomplikowane, ale także łatwo rozwiązane, jeśli znasz wszystkie formuły.

Jak znaleźć kwadrat kwadratu opisanego w pobliżu okręgu o danym promieniu?

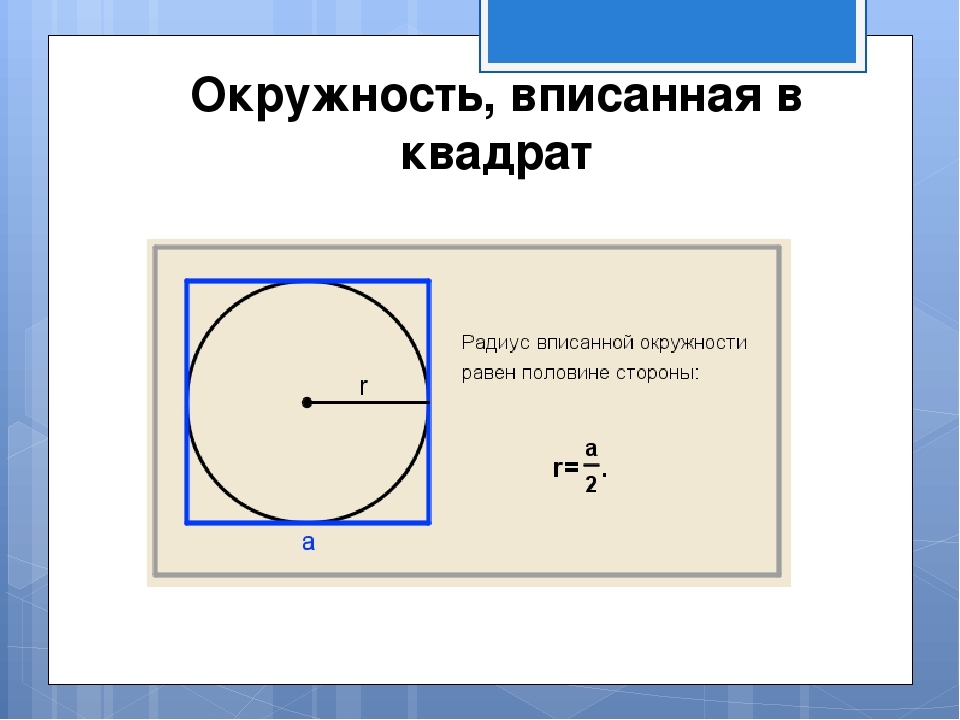
Zdjęcie pokazuje, że promień wpisanego okręgu jest równy połowy boku. Strona znajduje się zgodnie z odwrotną formułą, która jest pokazana na zdjęciu: a \u003d 2*r. Następnie znajdujemy kwadrat opisany w pobliżu okręgu o danym promieniu zgodnie ze wzorem S \u003d i kwadrat. Rozwiązanie:

• Załóżmy, że promień wynosi 7. Strona kwadratu A wynosi 2*7 \u003d 14.
• S \u003d 14 na placu \u003d 196.

Jeśli rozumiesz esencję rozwiązywania takich problemów, możesz je rozwiązać szybko i po prostu. Spójrzmy na kilka kolejnych przykładów.

Przykłady rozwiązywania problemów na temat „kwadratowy”

Aby naprawić pokryty materiał i zapamiętać wszystkie wzory, konieczne jest rozwiązanie kilku przykładów problemów na temat „kwadratowego kwadratowego”. Zaczynamy od prostego zadania i przechodzimy do rozwiązania bardziej złożonych:

Teraz wiesz, jak użyć formuły kwadratu, co oznacza, że \u200b\u200bmożesz wykonać każde zadanie. Sukces w przyszłym szkoleniu!

Wideo: Obliczanie powierzchni kwadratowych