Hogyan lehet megoldani a mozgásokat? A sebesség, az idő és a távolság közötti függőség képlete. Feladatok és megoldások.
Tartalom
- Az idő, a sebesség és a távolság függőségének képlete a 4. osztályban: Hogyan lehet a sebesség, az idő, a távolság?
- Hogyan lehet időt találni, tudni a sebességet és a távolságot?
- Hogyan lehet megtalálni a sebességet, ha az idő és a távolság ismert?
- Hogyan lehet megtalálni a távolságot, ha az idő és a sebesség ismert?
- A test sebességének grafikonja időben: Fotó
- 4. táblázat Osztály: sebesség, idő, távolság
- Példák a problémák megoldására a sebesség, az idő, a távolság a 4. fokozathoz
- Videó: Mozgási feladatok
Az idő, a sebesség és a távolság függőségének képlete a 4. osztályban: Hogyan lehet a sebesség, az idő, a távolság?
Az emberek, állatok vagy autók bizonyos sebességgel mozoghatnak. Egy bizonyos idő alatt eljuthatnak egy bizonyos utakon. Például: Ma fél órán belül elérheti az iskoláját. Bizonyos sebességgel megy, és 30 perc alatt legyőzi az 1000 métert. A legyőzött utat a matematikában jelölik S.- A sebességet a betű jelzi v- És az az idő, amelyre az utat elutasították, a levél jelzi t.
- Pálya - S.
- Sebesség- v
- Idő - t
Ha késik az iskolába, ugyanúgy mehet 20 perc alatt, növelve a sebességet. Tehát ugyanez az út különböző időpontokban és különböző sebességgel haladhat meg.
Hogyan függ az átjárási idő a sebességtől?
Minél nagyobb a sebesség, annál gyorsabb lesz a távolság. És minél alacsonyabb a sebesség, annál több időre van szüksége.

Hogyan lehet időt találni, tudni a sebességet és a távolságot?
Annak érdekében, hogy megtalálja az út eléréséhez szükséges időt, tudnia kell a távolságot és a sebességet. Ha a távolságot sebességre osztják, akkor megtudhatja az időt. Példa egy ilyen feladatra:
A nyúl feladata. A nyúl egy kilométerenként 1 kilométer sebességgel elmenekült a farkasból. 3 kilométerre futott a lyukához. Mikor érte el a nyúl a lyukat?

Hogyan lehet könnyű megoldani a mozgás problémáit, ahol meg kell találnia a távolságot, az időt vagy a sebességet?
- Óvatosan olvassa el a feladatot, és határozza meg, mi az ismert a probléma feltételeiből.
- Írja be ezeket az adatokat a tervezetre.
- Írja meg azt is, hogy mi ismeretlen és mit kell megtalálni
- Használja a képletet a távolságra, az időre és a sebességre vonatkozó feladatokhoz
- Írja be az ismert adatokat a képletbe, és oldja meg a problémát
Megoldás a nyúl és a farkas problémájára.
- A probléma körülményei alapján meghatározzuk, hogy tudjuk -e a sebességet és a távolságot.
- Ezenkívül a probléma körülményei alapján megállapítjuk, hogy meg kell találnunk azt az időt, amelyre a nyúlnak a lyuk eléréséhez szükséges.

Írjuk a vázlatot ezekre az adatokra, például:
Távolság Nora -tól - 3 kilométer
Nyúlsebesség - 1 kilométer 1 perc alatt
Az idő ismeretlen
Most ugyanazokat a matematikai jeleket írjuk le:
S. - 3 kilométer
V - 1 km/perc
t — ?
Emlékeztetünk és írunk egy képletet, hogy megtaláljuk az időt a notebookban:
t \u003d S: v
Most felírjuk a probléma megoldásának megoldását a számokkal:
t \u003d 3: 1 \u003d 3 perc
Hogyan lehet megtalálni a sebességet, ha az idő és a távolság ismert?
Annak érdekében, hogy megtalálják a sebességet, ha az idő és a távolság ismert, a távolságot egy ideig meg kell osztani. Példa egy ilyen feladatra:
A nyúl elmenekült a farkasból, és 3 kilométerre futott a lyukához. 3 perc alatt legyőzte ezt a távolságot. Milyen sebességgel futott a nyúl?
A mozgás problémájának megoldása:
- A tervezetben azt írjuk, hogy tudjuk a távolságot és az időt.
- A feladat körülményei alapján meghatározzuk, mit kell találni a sebességgel
- Ne feledje a sebesség megtalálásának képletét.
Az ilyen problémák megoldására szolgáló képleteket az alábbi kép mutatja.
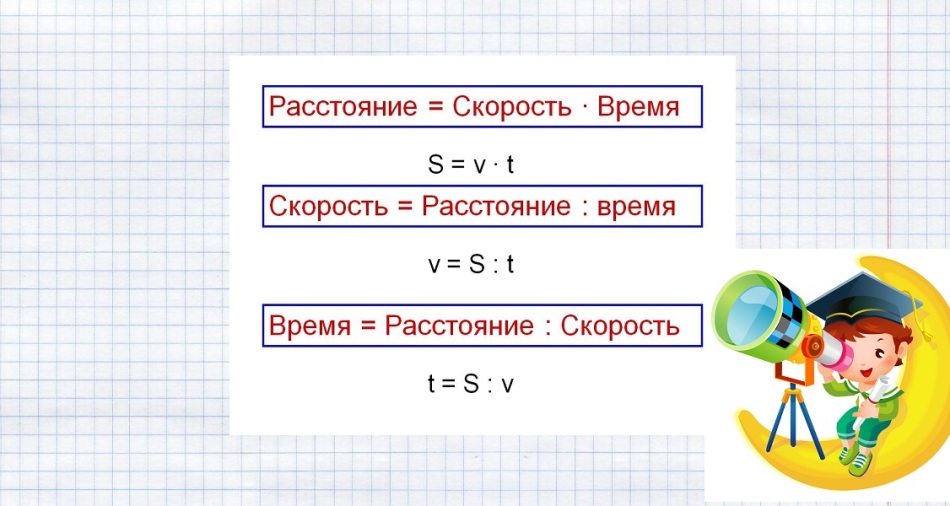
Az ismert adatokat helyettesítjük és megoldjuk a problémát:
Távolság Nora -tól - 3 kilométer
Az az idő, amikor a mezei nyúl elérte a lyukat - 3 perc
A sebesség ismeretlen
Ezeket az ismert adatokat matematikai jelekkel írjuk le
S. - 3 kilométer
t - 3 perc
v -?
Rögzítse a képletet a sebesség megtalálásához
v \u003d s: t
Most felírjuk a probléma megoldásának megoldását a számokkal:
v \u003d 3: 3 \u003d 1 km/perc

Hogyan lehet megtalálni a távolságot, ha az idő és a sebesség ismert?
A távolság megkereséséhez, ha az ismert idő és sebesség, akkor meg kell szorozni a sebességgel. Példa egy ilyen feladatra:
A nyúl 1 perc alatt 1 kilométer sebességgel elmenekült a farkasból. A lyukhoz való futáshoz három percre volt szüksége. Milyen távolságra futott a nyúl?
A probléma megoldása: Olyan tervezetben írunk, amelyet a probléma feltételeiből tudunk:
Nyúlsebesség - 1 kilométer 1 perc alatt
Az az idő, amikor a mezei nyúl Norába menekült
A távolság ismeretlen
Most ugyanazt fogjuk írni matematikai jelekkel:
v - 1 km/perc
t - 3 perc
S -?
Ne feledje a távolság megtalálásának képletét:
S \u003d v ⋅ t
Most felírjuk a probléma megoldásának megoldását a számokkal:
S \u003d 3 ⋅ 1 \u003d 3 km

Hogyan lehet megtanulni a bonyolultabb problémák megoldását?
A bonyolultabb feladatok megoldásának megtanulásához meg kell értenie, hogyan oldják meg az egyszerű feladatokat, ne feledje, hogy mely jelek jelzik a távolságot, a sebességet és az időt. Ha nem lehet emlékezni a matematikai képletekre, akkor azokat egy papírlapra kell írni, és mindig kéznél kell tartani a problémák megoldása közben. Oldja meg gyermekével egyszerű feladatokat, amelyeket útközben feltalálhat, például sétára.

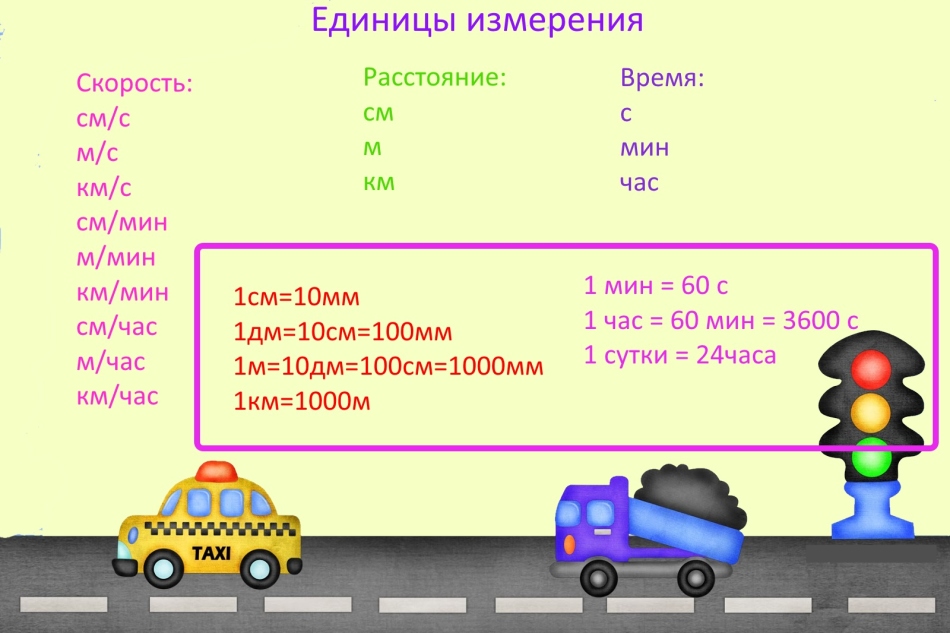
Egységek
Amikor megoldják a sebesség, az idő és a távolság problémáit, gyakran hibát követnek el, mivel elfelejtették lefordítani a mérési egységeket.
FONTOS: A mérési egységek bármilyen lehetnek, de ha egy feladatban különböző mérési egységek vannak, akkor azokat lefordítsuk. Például, ha a sebességet kilométerenként mérik, akkor a távolságot kilométerben és az időt percben kell bemutatni.
Kíváncsi: Az általánosan elfogadott intézkedésrendszert metrikusnak nevezzük, de nem mindig volt ez a helyzet, és a régi időkben Rus más méretegységeit használták.

A boák feladata: Az elefánt és a majom lépésekkel mérte a Boa -szűkítő hosszát. Egymás felé költöztek. A majom sebessége egy másodperc alatt 60 cm volt, az elefántsebesség pedig egy másodperc alatt 20 cm. 5 másodpercet töltöttek a mérésen. Mekkora a Boa Constrictor hossza? (döntés a kép alatt)

Megoldás:
A probléma körülményei alapján meghatározzuk, hogy tudjuk -e a majom és az elefánt sebességét, valamint azt az időt, amelyre szükségük van a boaver hosszának megméréséhez.
Leírjuk ezeket az adatokat:
Majomsebesség - 60 cm/s
Elefántsebesség - 20 cm/s
Idő - 5 másodperc
A távolság ismeretlen
Ezeket az adatokat matematikai jelekkel írjuk:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 másodperc
S -?
Írjuk a távolság képletét, ha a sebesség és az idő ismert:
S \u003d v ⋅ t
Kiszámoljuk, hogy a majom milyen távolságra ment:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Most számoljuk ki, hogy az elefánt mennyire telt el:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Összefoglaljuk azt a távolságot, amelyet a majom és az elefánt mentén ment:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
A test sebességének grafikonja időben: Fotó
A különböző sebességgel leküzdött távolságot különböző időpontokban legyőzik. Minél nagyobb a sebesség, annál kevesebb időbe telik.
4. táblázat Osztály: sebesség, idő, távolság
Az alábbi táblázat bemutatja azokat az adatokat, amelyekhez problémákkal kell felmerülnie, majd megoldani.
| № | Sebesség (km/óra) | Idő (óra) | Távolság (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Megtalálhatja és előállíthatja az asztal feladatait. Az alábbiakban bemutatjuk a feladatok feltételeinek lehetőségeit:
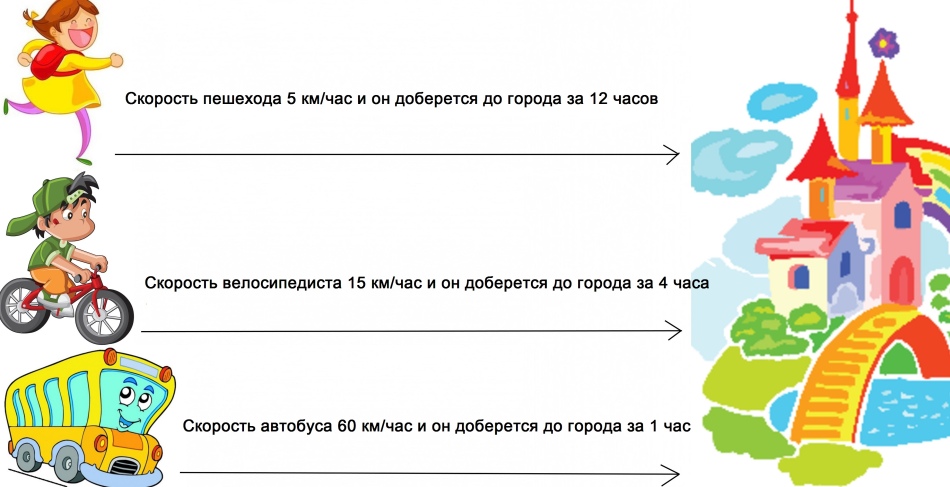
- Anya piros kalapot küldött a nagymamájának. A lányt folyamatosan zavarták, és lassan sétáltak át az erdőn, 5 km/h sebességgel. 2 órát töltött az úton. Milyen távolságra telt el egy piros sapka ebben az időben?
- A postás Pechkin egy csomagot vesz egy kerékpáron 12 km/h sebességgel. Tudja, hogy a háza és a Fedor bácsi háza közötti távolság 12 km. Segítsen Pechkinnek kiszámítani, mennyi időre lesz szükség az úton?
- Apu Ksyusha vásárolt egy autót, és úgy döntött, hogy elviszi családját a tengerbe. Az autó 60 km/h sebességgel vezette, és 4 órát töltöttek az úton. Mi a távolság a Ksyusha ház és a tengerpart között?
- A kacsák az ékben összegyűltek és a meleg szélekbe repültek. A madarak 3 órán át fáradtak a szárnyukról, és ebben az időben 300 km -re legyőzték. Mekkora volt a madarak sebessége?
- Az AN-2 repülőgép 220 km/h sebességgel repül. Kihúzódott Moszkvából, és Nizhny Novgorod felé repül, e két város közötti távolság 440 km. Meddig fog menni a repülőgép?

A fenti feladatokra adott válaszok az alábbi táblázatban találhatók:
| № | Sebesség (km/óra) | Idő (óra) | Távolság (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Példák a problémák megoldására a sebesség, az idő, a távolság a 4. fokozathoz
Ha egy feladatban több mozgás tárgya van, akkor meg kell tanítania a gyermeket, hogy vegye figyelembe ezen objektumok mozgását külön -külön, és csak akkor. Példa egy ilyen feladatra:
Vadik két barátja és a téma úgy döntött, hogy sétál, és házukat egymás felé hagyta. Vadik kerékpározott, és a téma sétált. Vadik 10 km/h sebességgel lovagolt, és a téma 5 km/óra sebességgel ment. Egy órával később találkoztak. Mi a távolság Vadik házai és témái között?
Ez a probléma megoldható a távolság sebességétől és az időtől való függésének képletével.
S \u003d v ⋅ t
Az a távolság, amelyet Vadik kerékpáron hajtott, megegyezik a sebességével, szorozva az utazással.
S \u003d 10 ⋅ 1 \u003d 10 kilométer
Hasonlóképpen tekintik a témát átadott távolságot:
S \u003d v ⋅ t
A sebesség és az idő digitális értékeit a képletbe helyettesítjük
S \u003d 5 ⋅ 1 \u003d 5 kilométer
A Vadik által elhajtott távolságot hozzá kell adni a téma átadott távolsághoz.
10 + 5 \u003d 15 kilométer
Hogyan lehet megtanulni, hogyan lehet megoldani az összetett problémákat, és megoldani kell, amelyekre logikusan gondolkodnia kell?
A gyermek logikus gondolkodásának fejlesztéséhez egyszerű, majd összetett logikai feladatokat kell megoldania. Ezek a feladatok több szakaszból állhatnak. Csak az egyik szakaszból a másikra mozoghat, ha az előző megoldódik. Példa egy ilyen feladatra:
Anton 12 km/h sebességgel kerékpározott, és Lisa egy robogón lovagolt, 2 -szer kevesebb sebességgel, mint Antoné, és Denis kétszer kevesebb sebességgel sétált, mint Lisaé. Mi a Denis sebessége?
A probléma megoldásához először meg kell tudnia Lisa sebességét, és csak azt követően Denis sebességét.

Néha a 4 fokozatú tankönyvekben nehéz feladatok vannak. Példa egy ilyen feladatra:
Két kerékpáros különböző városokat hagyott egymás felé. Az egyik sietett, és 12 km/h sebességgel rohant, a második lassan 8 km/h sebességgel lovagolt. A városok közötti távolság, ahonnan a kerékpárosok 60 km -t hagytak el. Milyen távolságra halad az egyes kerékpárosok, mielőtt találkoznának? (döntés a fotó alatt)

Megoldás:
- 12+8 \u003d 20 (km/h) a két kerékpáros teljes sebessége, vagy az a sebesség, amellyel közeledtek egymáshoz
- 60 : 20 \u003d 3 (óra) - Ez az az idő, amikor a kerékpárosok találkoztak
- 3 ⋅ 8 \u003d 24 (km) az a távolság, amelyet az első kerékpáros hajtott
- 12 ⋅ 3\u003d 36 (km) az a távolság, amelyet a második kerékpáros hajtott
- Ellenőrizze: 36+24 \u003d 60 (km) az a távolság, amelyet két kerékpáros megtett.
- Válasz: 24 km, 36 km.
Kínáljon gyermekeket játék formájában az ilyen problémák megoldására. Lehet, hogy ők maguk akarják összeállítani a barátokkal, állatokkal vagy madarakkal kapcsolatos feladatukat.







