Kako riješiti pokrete za pokret? Formula ovisnosti između brzine, vremena i udaljenosti. Zadaci i rješenja.
Sadržaj
- Formula za ovisnost vremena, brzine i udaljenosti tijekom 4. razreda: Kako je brzina, vrijeme, udaljenost?
- Kako pronaći vrijeme, poznavanje brzine i udaljenosti?
- Kako pronaći brzinu ako je poznato vrijeme i udaljenost?
- Kako pronaći udaljenost ako se znaju i brzina?
- Grafikon brzine tijela na vrijeme: fotografija
- Tablica 4 Klasa: Brzina, vrijeme, udaljenost
- Primjeri rješavanja problema za brzinu, vrijeme, udaljenost za stupanj 4
- VIDEO: Zadaci pokreta
Formula za ovisnost vremena, brzine i udaljenosti tijekom 4. razreda: Kako je brzina, vrijeme, udaljenost?
Ljudi, životinje ili automobili mogu se kretati određenom brzinom. Neko vrijeme mogu ići određenim putem. Na primjer: Danas možete doći do svoje škole za pola sata. Idete određenom brzinom i prevladate 1000 metara u 30 minuta. Put koji se prevlada S.. Brzina je naznačena slovom v. A vrijeme za koje je odbijen put označeno je slovom t.
- Staza - S.
- Brzina- V
- Vrijeme - t
Ako kasnite u školu, možete ići istim putem za 20 minuta, povećavajući brzinu. Dakle, isti put se može proći kroz različita vremena i različitim brzinama.
Kako vrijeme prolaska ovisi o brzini?
Što je veća brzina, brže će se napraviti udaljenost. I što je niža brzina, više vremena trebate proći stazu.

Kako pronaći vrijeme, poznavanje brzine i udaljenosti?
Da biste pronašli vrijeme koje trebate proći stazu, morate znati udaljenost i brzinu. Ako je udaljenost podijeljena na brzinu, saznat ćete vrijeme. Primjer takvog zadatka:
Zadatak zeca. Zec je pobjegao od vuka brzinom od 1 kilometra u minuti. Trčao je do svoje rupe 3 kilometra. U koje vrijeme je zec dosegao rupu?

Kako je lako riješiti probleme kretanja, gdje trebate pronaći udaljenost, vrijeme ili brzinu?
- Pažljivo pročitajte zadatak i odredite što je poznato iz uvjeta problema.
- Nacrt napišite ove podatke.
- Također napišite ono što je nepoznato i što treba pronaći
- Koristite formulu za zadatke o udaljenosti, vremenu i brzini
- Unesite poznate podatke u formulu i riješite problem
Rješenje za problem oko zeca i vuka.
- Iz uvjeta problema utvrđujemo da znamo brzinu i udaljenost.
- Također, iz uvjeta problema, utvrđujemo da trebamo pronaći vrijeme koje je zec trebao doći do rupe.

Nacrtamo nacrt ovih podataka, na primjer,:
Udaljenost do rupe - 3 kilometra
Brzina zeca - 1 kilometar u 1 minuti
Vrijeme je nepoznato
Sada pišemo isto kao i matematički znakovi:
S. - 3 kilometra
V - 1 km/min
t — ?
Sjećamo se i pišemo formulu kako bismo pronašli vrijeme u bilježnici:
t \u003d s: v
Sada zapišemo rješenje problema s brojevima:
t \u003d 3: 1 \u003d 3 minute
Kako pronaći brzinu ako je poznato vrijeme i udaljenost?
Da biste pronašli brzinu, ako su poznate vrijeme i udaljenost, udaljenost se mora neko vrijeme podijeliti. Primjer takvog zadatka:
Zec je pobjegao od vuka i potrčao do svoje rupe 3 kilometra. Prevladao je ovu udaljenost za 3 minute. Kojom brzinom je radio zec?
Rješavanje problema pokreta:
- U nacrtu zapisujemo da znamo udaljenost i vrijeme.
- Iz uvjeta problema određujemo što treba pronaći brzinu
- Sjetite se formule za pronalaženje brzine.
Formule za rješavanje takvih problema prikazane su na donjoj slici.
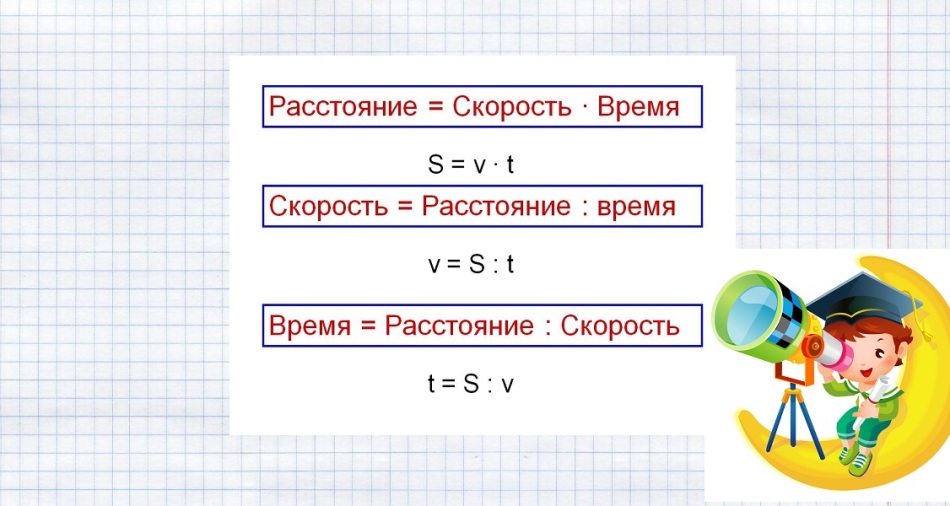
Zamjenjujemo poznate podatke i riješimo problem:
Udaljenost do rupe - 3 kilometra
Vrijeme za koje je zec dosegao rupu je 3 minute
Brzina je nepoznata
Te poznate podatke pišemo matematičkim znakovima
S. - 3 kilometra
t - 3 minute
v -?
Zabilježite formulu da biste pronašli brzinu
v \u003d s: t
Sada zapišemo rješenje problema s brojevima:
v \u003d 3: 3 \u003d 1 km/min

Kako pronaći udaljenost ako se znaju i brzina?
Da biste pronašli udaljenost, ako je poznato vrijeme i brzinu, potrebno je umnožiti brzinom. Primjer takvog zadatka:
Zec je pobjegao od vuka brzinom od 1 kilometar u 1 minuti. Trebalo mu je tri minute da pobjegne do rupe. Koju je udaljenost prolazila zec?
Rješenje problema: Pišemo na nacrt koji znamo iz uvjeta problema:
Brzina zeca - 1 kilometar u 1 minuti
Vrijeme kad je zec pobjegao u Noru je 3 minute
Udaljenost je nepoznata
Sada ćemo istu stvar napisati matematičkim znakovima:
v - 1 km/min
t - 3 minute
S -?
Sjetite se formule za pronalaženje udaljenosti:
S \u003d v ⋅ t
Sada zapišemo rješenje problema s brojevima:
S \u003d 3 ⋅ 1 \u003d 3 km

Kako naučiti riješiti složenije probleme?
Da biste naučili kako riješiti složenije zadatke, morate shvatiti kako se rješavaju jednostavni zadaci, sjetite se koji znakovi ukazuju na udaljenost, brzinu i vrijeme. Ako nije moguće zapamtiti matematičke formule, treba ih napisati na listu papira i uvijek se držati pri ruci dok rješavaju probleme. Riješite s djetetom jednostavnim zadacima koji se mogu izmisliti, na primjer, tijekom šetnje.

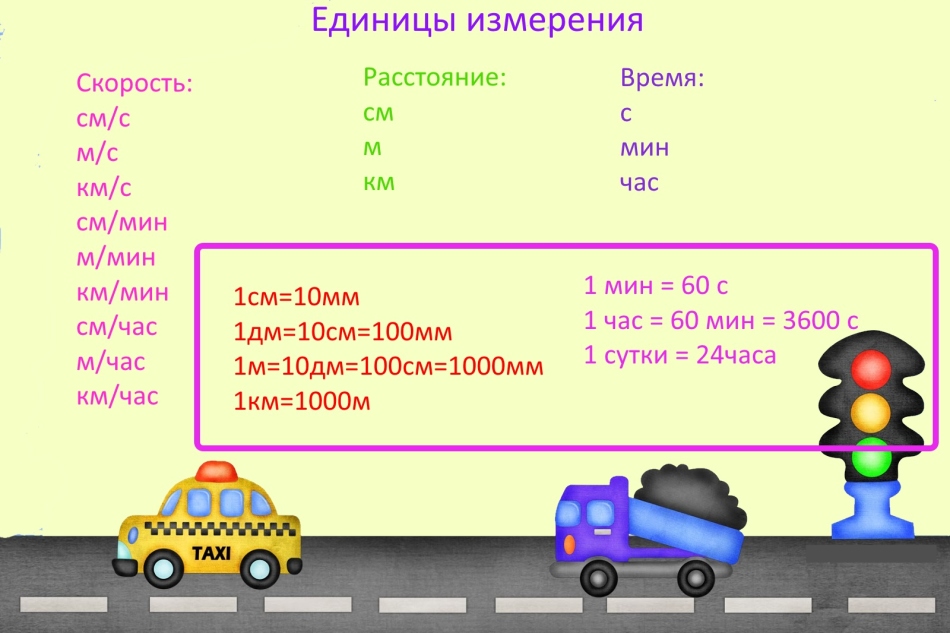
Jedinice
Kada rješavaju probleme oko brzine, vremena i udaljenosti, često pogriješe, zbog činjenice da su zaboravili prevesti mjerne jedinice.
Važno: mjerne jedinice mogu biti bilo koje, ali ako postoje različite jedinice mjerenja u jednom zadatku, prevedite ih isto. Na primjer, ako se brzina mjeri u kilometrima u minuti, tada se udaljenost mora predstaviti u kilometrima, a vrijeme za nekoliko minuta.
Za znatiželjan: Općenito prihvaćeni sustav mjera naziva se metrikom sada, ali to nije uvijek bio slučaj, a u stara vremena u Rusiji korištene su i druge dimenzije.

Zadatak boa: Slon i majmun mjerili su duljinu boa constrictor koracima. Krenuli su jedni prema drugima. Brzina majmuna bila je 60 cm u jednoj sekundi, a brzina slona je 20 cm u jednoj sekundi. Proveli su 5 sekundi na mjerenje. Kolika je duljina boa constrictor? (Odluka ispod slike)

Riješenje:
Iz uvjeta problema, utvrđujemo da znamo brzinu majmuna i slona i vremena koje su im trebali mjeriti duljinu pojačanja.
Ove podatke zapišemo:
Brzina majmuna - 60 cm/s
Brzina slona - 20 cm/s
Vrijeme - 5 sekundi
Udaljenost je nepoznata
Te podatke pišemo matematičkim znakovima:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 sekundi
S -?
Napišimo formulu za udaljenost ako su poznata brzina i vrijeme:
S \u003d v ⋅ t
Izračunavamo koliko je majmun prošlo udaljenost:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Sada izračunajmo koliko je slon prošao:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Sažeti udaljenost koju je majmun i udaljenost koju je slon prošao:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
Grafikon brzine tijela na vrijeme: fotografija
Prevladavanje udaljenosti s različitim brzinama prevladava se u različitim vremenima. Što je veća brzina, manje će vremena trebati.
Tablica 4 Klasa: Brzina, vrijeme, udaljenost
Tablica u nastavku prikazuje podatke za koje trebate smisliti probleme, a zatim ih riješiti.
| № | Brzina (km/sat) | Vrijeme (sat) | Udaljenost (km) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Možete sami fantazirati i smisliti zadatke za stol. Ispod su naše mogućnosti za zadatke:
- Mama je poslala crveni šešir svojoj baki. Djevojčica se stalno ometala i polako je hodala šumom, brzinom od 5 km/h. Provela je 2 sata na stazi. Koju je udaljenost prošla crvena kapica za to vrijeme?
- Postman Pechkin uzima parcelu na biciklu brzinom od 12 km/h. Zna da je udaljenost između njegove kuće i kuće ujaka Fedora 12 km. Pomozite Pechkinu da izračunate koliko će vremena trebati za cestu?
- Tata Ksyusha kupio je automobil i odlučio odvesti svoju obitelj u more. Automobil je vozio brzinom od 60 km/h, a na cesti su provedeni 4 sata. Kolika je udaljenost između kuće Ksyusha i morske obale?
- Patke su se okupile u klinu i odletjele u tople rubove. Ptice su mahale krila umorna 3 sata i prevladale 300 km za to vrijeme. Kolika je bila brzina ptica?
- Zrakoplov An-2 leti brzinom od 220 km/h. Odletio je iz Moskve i letio u Nizhny Novgorod, udaljenost između ta dva grada iznosi 440 km. Koliko dugo će zrakoplov ići?

Odgovori na gore navedene zadatke mogu se naći u tablici ispod:
| № | Brzina (km/sat) | Vrijeme (sat) | Udaljenost (km) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Primjeri rješavanja problema za brzinu, vrijeme, udaljenost za stupanj 4
Ako u jednom zadatku postoji nekoliko objekata pokreta, morate naučiti dijete da razmatra kretanje ovih objekata odvojeno i tek tada zajedno. Primjer takvog zadatka:
Dvojica prijatelja Vadika i tema odlučili su se prošetati i ostaviti svoje kuće jedni prema drugima. Vadik je vozio bicikl, a tema je hodala. Vadik je jahao brzinom od 10 km/h, a tema je bila brzinom od 5 km na sat. Sat vremena kasnije upoznali su se. Kolika je udaljenost između Vadikovih kuća i tema?
Ovaj se problem može riješiti pomoću formule za ovisnost udaljenosti o brzini i vremenu.
S \u003d v ⋅ t
Udaljenost koju je Vadik vozio na biciklu bit će jednaka njegovoj brzini pomnoženoj s putovanjem.
S \u003d 10 ⋅ 1 \u003d 10 kilometara
Udaljenost koju je tema prošla smatra se slično:
S \u003d v ⋅ t
Digitalne vrijednosti njegove brzine i vremena zamjenjujemo u formulu
S \u003d 5 ⋅ 1 \u003d 5 kilometara
Udaljenost koju je Vadik vozio mora se dodati na udaljenost koju je tema prošla.
10 + 5 \u003d 15 kilometara
Kako naučiti kako riješiti složene probleme, za rješavanje koje trebate logično razmišljati?
Da biste razvili logično razmišljanje o djetetu, morate s njim riješiti jednostavne, a zatim složene logičke probleme. Ti se zadaci mogu sastojati od nekoliko faza. Moguće je preći iz jedne faze u drugu ako je prethodna riješena. Primjer takvog zadatka:
Anton je krenuo na bicikl brzinom od 12 km/h, a Lisa je jahala na skuteru brzinom od 2 puta manje od Antona, a Denis je hodao brzinom od 2 puta manje od Lise. Koja je Denisova brzina?
Da biste riješili ovaj problem, prvo morate saznati brzinu Lise i tek nakon te Denisove brzine.

Ponekad u udžbenicima za 4 razreda postoje teški zadaci. Primjer takvog zadatka:
Dva biciklista su međusobno napustila različite gradove. Jedan od njih požurio je i trkao brzinom od 12 km/h, a drugi je polako vozio brzinom od 8 km/h. Udaljenost između gradova iz kojih su biciklisti napustili 60 km. Koju će udaljenost proći svaki biciklista, prije nego što se sretne? (Odluka na fotografiji)

Riješenje:
- 12+8 \u003d 20 (km/h) je ukupna brzina dva biciklista ili brzina s kojom su se približavali
- 60 : 20 \u003d 3 (sati) - ovo je vrijeme kroz koje su se sastali biciklisti
- 3 ⋅ 8 \u003d 24 (km) je udaljenost koju je prvi biciklista vozio
- 12 ⋅ 3\u003d 36 (km) je udaljenost koju je drugi biciklista vozio
- Provjerite: 36+24 \u003d 60 (km) je udaljenost koju su dva biciklista putovala.
- Odgovor: 24 km, 36 km.
Ponudite djecu u obliku igre za rješavanje takvih problema. Možda će oni sami htjeti sastaviti svoj zadatak o prijateljima, životinjama ili pticama.







