¿Cómo encontrar un área cuadrada si se conoce el perímetro, diagonal? Cómo encontrar el cuadrado del cuadrado inscrito en el círculo y descrito cerca de la circunferencia: fórmula, ejemplos de problemas de resolución. ¿Cómo encontrar el lado y la diagonal de la plaza, si se conoce su área?

Lea el artículo para saber cómo encontrar el área cuadrada de diferentes maneras.

Contenido

Un cuadrado es un rectángulo equilibrado. Este cuadrilátero adecuado y plano tiene igualdad en todos los lados, esquinas y diagonales. Debido al hecho de que existe tal igualdad, la fórmula para calcular el área y otras características se modifica ligeramente en comparación con otras figuras matemáticas. Pero esto no hace que las tareas sean demasiado complicadas. Analicemos todas las fórmulas y soluciones a este artículo.

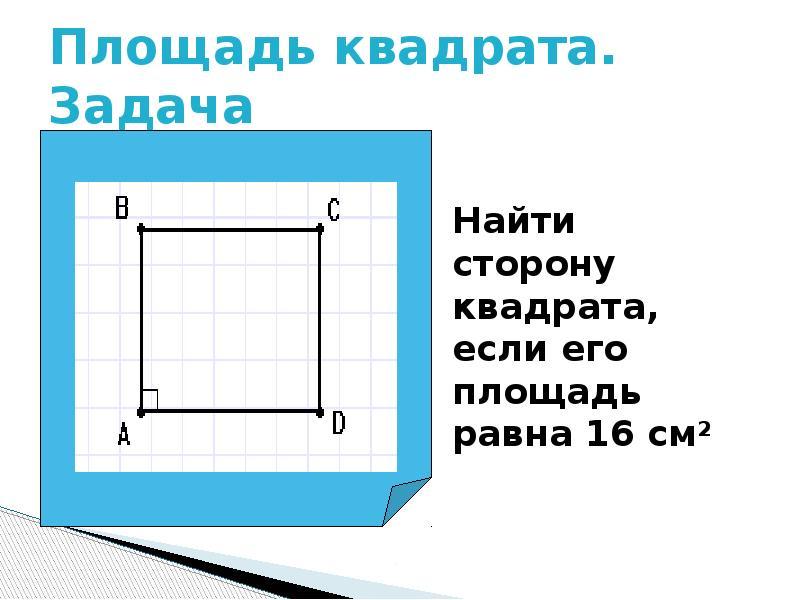
¿Cómo encontrar el lado de la plaza, conociendo su área?

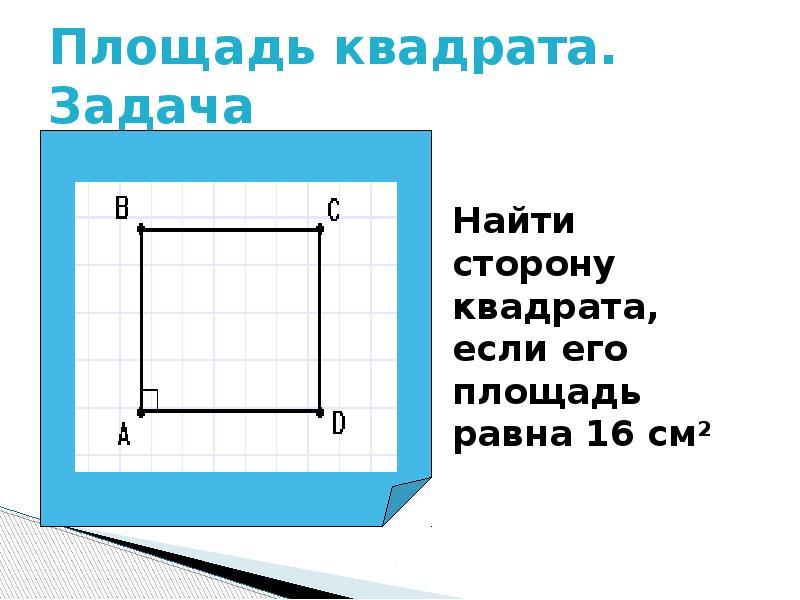
Área S. Los cuadrados directos y cuadrados se calculan mediante la fórmula: a Multiplicar por b.. Pero dado que la plaza tiene una igualdad completa de las partes, su área será igual: S \u003d (a) en segundo grado.¿Cómo averiguar el tamaño del lado de la plaza, conociendo su área?

Si se conoce el área del cuadrado cuadrado, entonces encontramos el lado calculando el área desde debajo de la raíz cuadrada.
Por ejemplo, el área del cuadrado es 49, ¿a qué es el lado igual?
49 \u003d (a) en segundo grado. Decisión: a \u003d raíz de 49 \u003d 7. Respuesta: 7.

Si necesita encontrar el lado del cuadrado cuadrado, cuyo área es demasiado larga, entonces use la calculadora. Primero marque el número de área y luego presione el signo raíz en el teclado de la calculadora. El número resultante será la respuesta.

¿Cómo encontrar una diagonal cuadrada si se conoce su área?

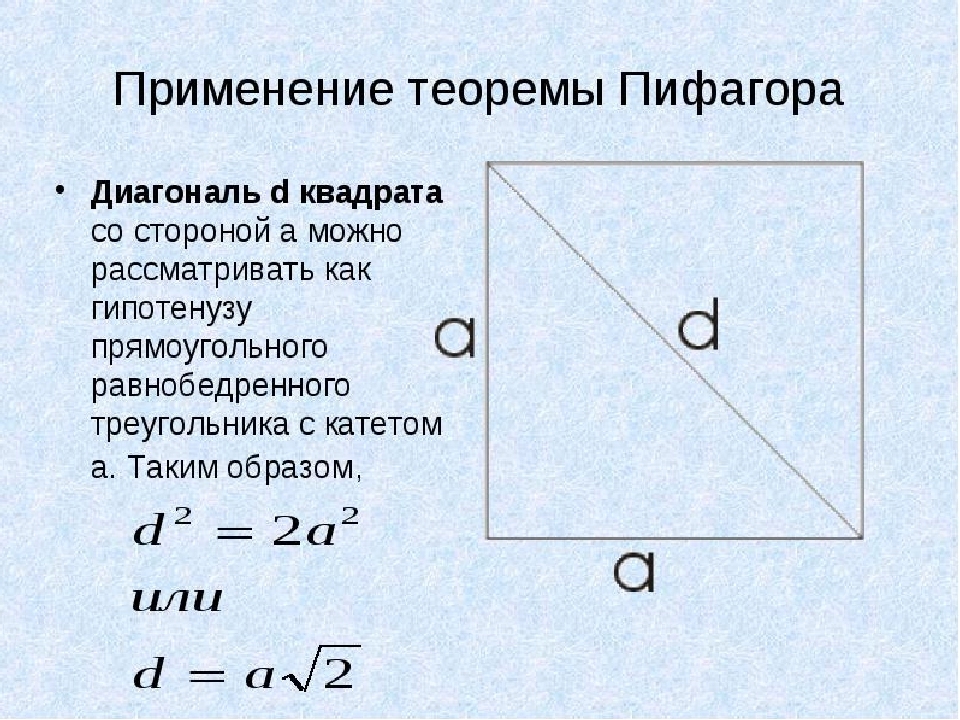
En este ejemplo, usaremos el teorema de Pitágoras. En un cuadrado, todos los lados son iguales y la diagonal d. Consideraremos como una hipotenusa de un triángulo de isósceles rectangulares con una pierna a. Ahora encontramos una diagonal cuadrada si se conoce su área:

Para no pintar todo el teorema de Pitágoras, decidiremos sobre la segunda opción: d \u003d Aying, donde A es el lado del cuadrado.
Entonces, sabemos el área de la plaza, por ejemplo, es igual a 64. Entonces un lado a \u003d √64 \u003d 8.
Resulta D \u003d 8√2. La raíz de 2 no resulta todo el número, por lo que en la respuesta puede escribir de esta manera: d \u003d 8√2. Pero, si desea calcular el valor, use la calculadora: √2 \u003d 1.41421356237 y multiplicarse por 8, resulta 11, 3137084.

Importante: Por lo general, en las matemáticas, no quedan números con una gran cantidad de números en respuesta. Es necesario redondear o salir con la raíz. Por lo tanto, la respuesta a la diagonal es si el área es 64 de la siguiente manera: d \u003d 8√2.

¿Cómo encontrar un área cuadrada a través de una diagonal?

La fórmula para encontrar el área cuadrada a través de la diagonal es simple:

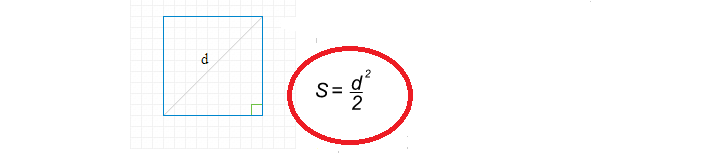
Ahora escribamos una solución para encontrar el área cuadrada a través de la diagonal:

Diagonal d \u003d 8.
8 en el cuadrado es 64.
64 divide por 2 igual 32.
El área cuadrada es de 32.

Consejo: Esta tarea tiene otra solución a través del teorema de Pitágoras, pero es más compleja. Por lo tanto, use la solución que examinamos.

¿Cómo encontrar un área cuadrada, conociendo su perímetro?

El perímetro del cuadrado cuadrado PAG. - Esta es la suma de todas las partes. Para encontrar su área, conociendo su perímetro, primero debe calcular el lado del cuadrado cuadrado. Decisión:

Supongamos que el perímetro es 24. Divida 24 en 4 lados, resulta 6: este es un lado.
Ahora usamos la fórmula para encontrar el área, sabiendo a qué se trata el lado del cuadrado cuadrado: S \u003d a en un cuadrado, s \u003d 6 en un cuadrado \u003d 36.
Respuesta: 36

Como puede ver, conociendo el perímetro de la plaza, solo encuentre su área.

¿Cómo encontrar un área de un cuadrado inscrito en un círculo con un radio dado?

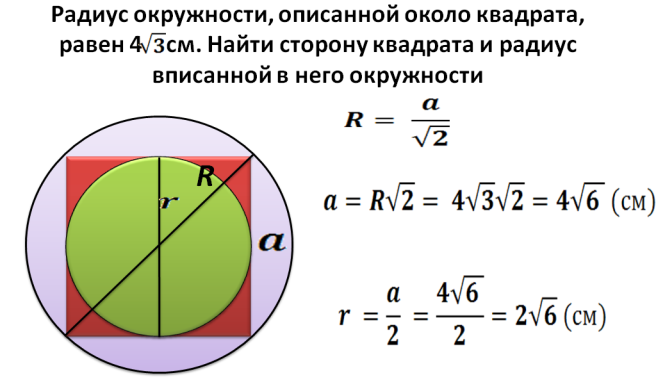
Radio Riñonal - Esta es la mitad de la diagonal de un cuadrado inscrito en un círculo. Ahora podemos encontrar una diagonal por la fórmula: d \u003d 2*r. A continuación, encontramos el cuadrado del cuadrado inscrito en un círculo con un radio dado:

La diagonal es 2 multiplicación por el radio. Por ejemplo, el radio es 5, entonces la diagonal es igual 2*5=10.
Se describió anteriormente cómo encontrar el cuadrado del cuadrado si se conoce la diagonal: S \u003d diagonal en un cuadrado dividido en 2. S \u003d 10*10 y divide por 2 \u003d 50.
Respuesta - 50.

Esta tarea es un poco más complicada, pero también se resuelve fácilmente si conoce todas las fórmulas.

¿Cómo encontrar un área de un cuadrado descrito cerca de un círculo con un radio dado?

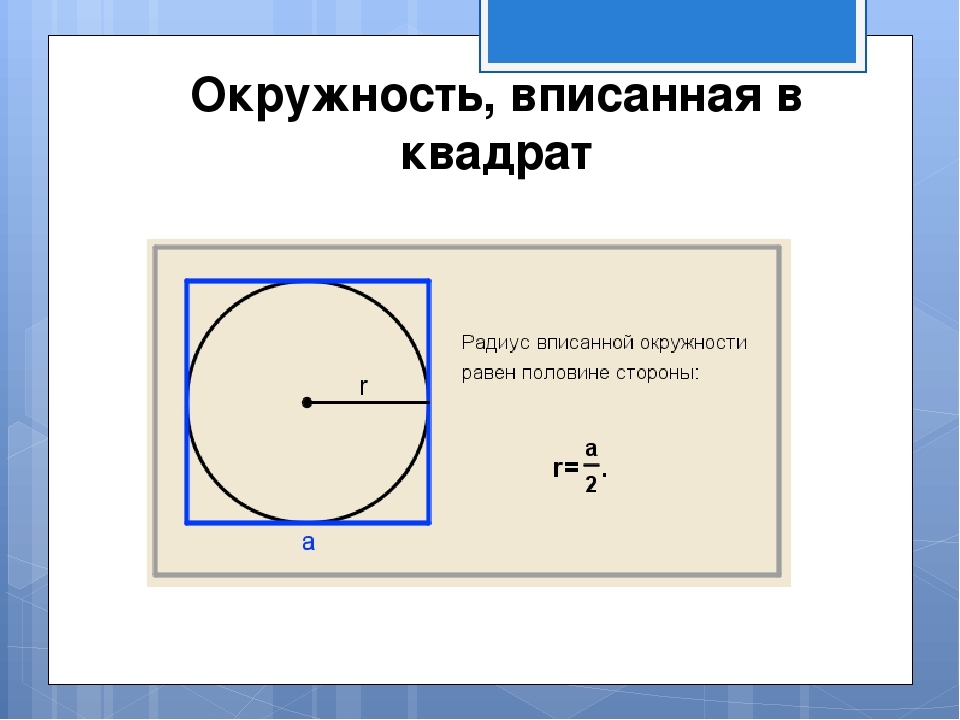
La imagen muestra que el radio del círculo inscrito es igual a la mitad del lado. El lado se encuentra de acuerdo con la fórmula inversa que se muestra en la imagen: a \u003d 2*r. Luego encontramos el área del cuadrado descrito cerca del círculo con un radio dado de acuerdo con la fórmula S \u003d y en un cuadrado. Decisión:

Supongamos que el radio es 7. El lado del cuadrado A es 2*7 \u003d 14.
S \u003d 14 en un cuadrado \u003d 196.

Si comprende la esencia de resolver tales problemas, puede resolverlos de manera rápida y simple. Veamos algunos ejemplos más.

Ejemplos de resolución de problemas sobre el tema "cuadrado cuadrado"

Para arreglar el material cubierto y recordar todas las fórmulas, es necesario resolver varios ejemplos de problemas sobre el tema del "área cuadrada". Comenzamos con una tarea simple y nos movemos a resolver más complejos: