Πώς να βρείτε μια τετραγωνική περιοχή εάν η περίμετρος είναι γνωστή, διαγώνια; Πώς να βρείτε το τετράγωνο του τετραγώνου εγγεγραμμένου στον κύκλο και περιγράφεται κοντά στην περιφέρεια: φόρμουλα, παραδείγματα επίλυσης προβλημάτων. Πώς να βρείτε την πλευρά και τη διαγώνιο της πλατείας, εάν η περιοχή της είναι γνωστή;

Διαβάστε το άρθρο για να μάθετε πώς να βρείτε την τετραγωνική περιοχή με διαφορετικούς τρόπους.

Ένα τετράγωνο είναι ένα ισόπλευρο ορθογώνιο. Αυτό το σωστό και επίπεδη τετράγωνο έχει ισότητα σε όλες τις πλευρές, τις γωνίες και τις διαγώνιες. Λόγω του γεγονότος ότι υπάρχει τέτοια ισότητα, ο τύπος για τον υπολογισμό της περιοχής και άλλων χαρακτηριστικών είναι ελαφρώς τροποποιημένη σε σύγκριση με άλλα μαθηματικά στοιχεία. Αλλά αυτό δεν κάνει τα καθήκοντα πολύ περίπλοκα. Ας αναλύσουμε όλους τους τύπους και τις λύσεις σε αυτό το άρθρο.

Πώς να βρείτε την πλευρά της πλατείας, γνωρίζοντας την περιοχή της;

τετράγωνο ΜΙΚΡΟ. Τα άμεσα και τετράγωνα τετράγωνα υπολογίζονται με τον τύπο: ένα Πολλαπλασιάστε με ΣΙ.. Αλλά δεδομένου ότι η πλατεία έχει μια πλήρη ισότητα των μερών, η περιοχή της θα είναι ίση: S \u003d (α) στο δεύτερο βαθμό.  Πώς να μάθετε το μέγεθος της πλευράς της πλατείας, γνωρίζοντας την περιοχή του;

• Εάν η περιοχή του τετραγώνου είναι γνωστή, τότε βρίσκουμε την πλευρά υπολογίζοντας την περιοχή από κάτω από την τετραγωνική ρίζα.
• Για παράδειγμα, η περιοχή της πλατείας είναι 49, τότε ποια είναι η πλευρά ίση με;
• 49 \u003d (α) στο δεύτερο βαθμό. Λύση: a \u003d ρίζα 49 \u003d 7. Απάντηση: 7.

Εάν πρέπει να βρείτε την πλευρά του τετραγώνου, η περιοχή της οποίας είναι πολύ μεγάλη, τότε χρησιμοποιήστε την αριθμομηχανή. Πρώτα καλέστε τον αριθμό της περιοχής και, στη συνέχεια, πατήστε το ριζικό σημάδι στο πληκτρολόγιο της αριθμομηχανής. Ο προκύπτων αριθμός θα είναι η απάντηση.

Πώς να βρείτε μια τετραγωνική διαγώνια εάν είναι γνωστή η περιοχή της;

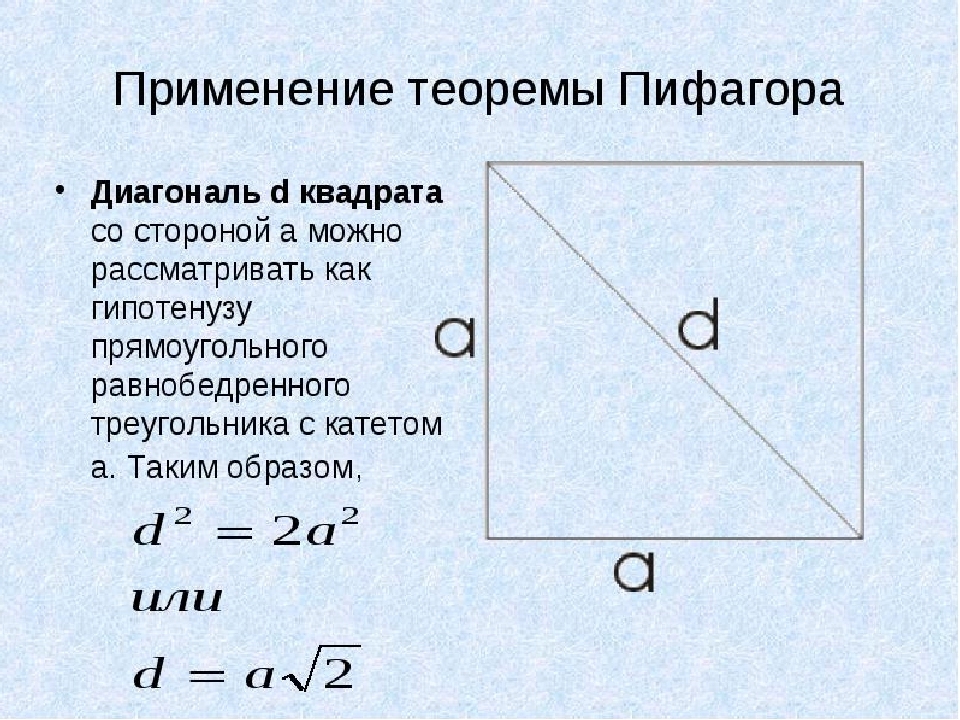
Σε αυτό το παράδειγμα, θα χρησιμοποιήσουμε το θεώρημα Pythagoras. Σε ένα τετράγωνο, όλες οι πλευρές είναι ίσες και η διαγώνια ΡΕ. Θα θεωρήσουμε ως υποτετάνιο ενός ορθογώνιου ισοσκελίου τρίγωνου με ένα πόδι ένα. Τώρα βρίσκουμε μια τετραγωνική διαγώνια εάν η περιοχή της είναι γνωστή:

• Προκειμένου να μην ζωγραφίσουμε ολόκληρο το θεώρημα της Πυθαγόρεης, θα αποφασίσουμε για τη δεύτερη επιλογή: d \u003d aising, όπου a είναι η πλευρά της πλατείας.
• Γνωρίζουμε λοιπόν την περιοχή της πλατείας, για παράδειγμα, είναι ίση με 64. Έτσι μία πλευρά a \u003d √64 \u003d 8.
• Αποδεικνύεται D \u003d 8√2. Η ρίζα των 2 δεν αποδείξει ολόκληρο τον αριθμό, οπότε στην απάντηση μπορείτε να γράψετε με αυτόν τον τρόπο: d \u003d 8√2. Αλλά, αν θέλετε να υπολογίσετε την τιμή, τότε χρησιμοποιήστε την αριθμομηχανή: √2 \u003d 1.41421356237 και πολλαπλασιάστε κατά 8, αποδεικνύεται 11, 3137084.

Σπουδαίος: Συνήθως, στα μαθηματικά, δεν έχουν παραμείνει αριθμοί με μεγάλο αριθμό αριθμών. Είναι απαραίτητο να στρογγυλοποιήσετε ή να αφήσετε τη ρίζα. Επομένως, η απάντηση στη διαγώνιο είναι εάν η περιοχή είναι 64 ως εξής: d \u003d 8√2.

Πώς να βρείτε μια τετράγωνη περιοχή μέσω μιας διαγώνιας;

Ο τύπος για την εύρεση της τετραγωνικής περιοχής μέσω της διαγώνιας είναι απλή:

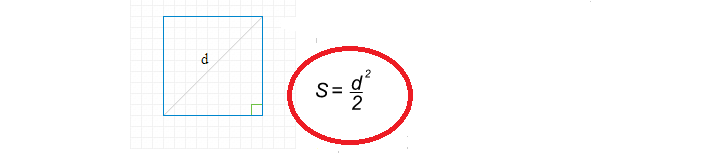
Τώρα ας γράψουμε μια λύση για να βρούμε την τετραγωνική περιοχή μέσω της διαγώνιας:

• Διαγώνια d \u003d 8.
• 8 στην πλατεία είναι 64.
• 64 Διαχωρίστε κατά 2 ίσο 32.
• Η τετράγωνη περιοχή είναι 32.

Συμβουλή: Αυτό το καθήκον έχει μια άλλη λύση μέσω του θεώρημα Pythagoras, αλλά είναι πιο περίπλοκο. Επομένως, χρησιμοποιήστε τη λύση που εξετάσαμε.

Πώς να βρείτε μια τετράγωνη περιοχή, γνωρίζοντας την περίμετρο της;

Η περίμετρος του τετραγώνου Π. - Αυτό είναι το άθροισμα όλων των μερών. Για να βρείτε την περιοχή της, γνωρίζοντας την περίμετρο της, πρέπει πρώτα να υπολογίσετε την πλευρά του τετραγωνικού τετραγώνου. Λύση:

• Ας υποθέσουμε ότι η περίμετρο είναι 24. Διαιρέστε 24 σε 4 πλευρές, αποδεικνύεται 6 - Αυτή είναι η μία πλευρά.
• Τώρα χρησιμοποιούμε τον τύπο για την εύρεση της περιοχής, γνωρίζοντας ποια είναι η πλευρά της πλατείας της πλατείας ίση με: S \u003d a σε τετράγωνο, s \u003d 6 σε τετράγωνο \u003d 36.
• Απάντηση: 36

Όπως μπορείτε να δείτε, γνωρίζοντας την περίμετρο της πλατείας, απλά βρείτε την περιοχή της.

Πώς να βρείτε μια περιοχή ενός τετραγώνου εγγεγραμμένου σε έναν κύκλο με δεδομένη ακτίνα;

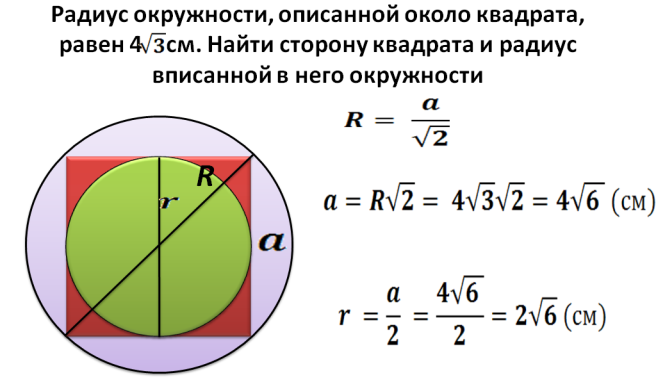
Ακτίνα κύκλου R - Αυτή είναι η μισή διαγώνιο ενός τετραγώνου που έχει εγγραφεί σε έναν κύκλο. Τώρα μπορούμε να βρούμε μια διαγώνια από τον τύπο: d \u003d 2*r. Στη συνέχεια, βρίσκουμε το τετράγωνο του τετραγώνου εγγεγραμμένου σε έναν κύκλο με μια δεδομένη ακτίνα:

• Η διαγώνια είναι 2 πολλαπλασιασμένα με την ακτίνα. Για παράδειγμα, η ακτίνα είναι 5, τότε η διαγώνια είναι ίση 2*5=10.
• Περιγράφηκε παραπάνω πώς να βρείτε το τετράγωνο της πλατείας εάν η διαγώνια είναι γνωστή: S \u003d διαγώνιο σε ένα τετράγωνο χωρισμένο σε 2. s \u003d 10*10 και διαιρέστε κατά 2 \u003d 50.
• Απάντηση - 50.

Αυτό το καθήκον είναι λίγο πιο περίπλοκο, αλλά και εύκολα επιλυθεί αν γνωρίζετε όλους τους τύπους.

Πώς να βρείτε μια περιοχή ενός τετραγώνου που περιγράφεται κοντά σε έναν κύκλο με δεδομένη ακτίνα;

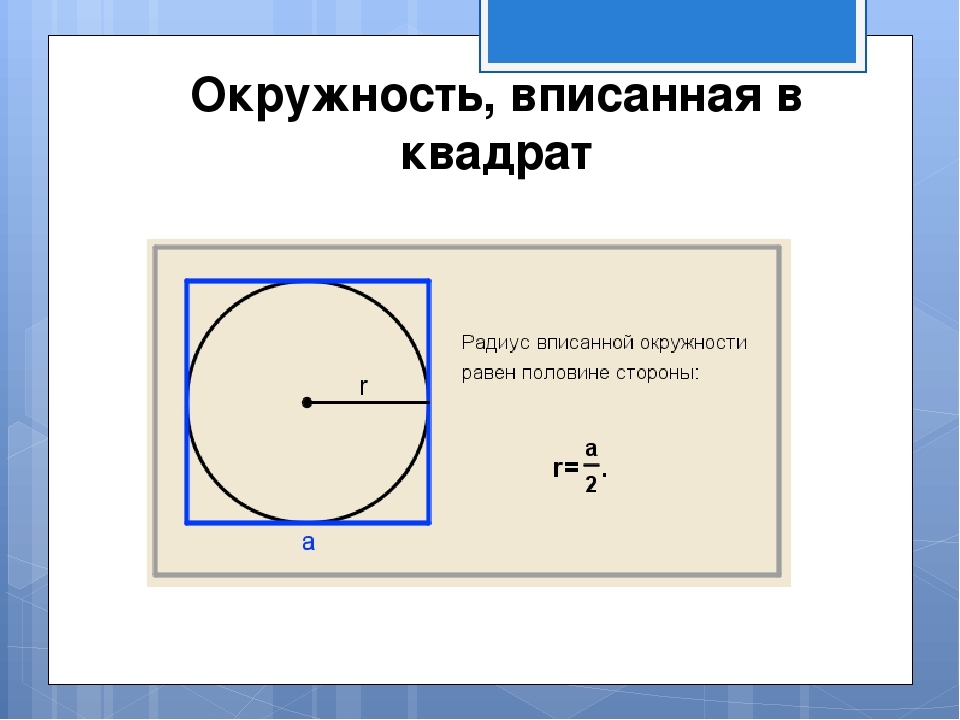
Η εικόνα δείχνει ότι η ακτίνα του εγγεγραμμένου κύκλου είναι ίση με το ήμισυ της πλευράς. Η πλευρά βρίσκεται σύμφωνα με την αντίστροφη φόρμουλα που απεικονίζεται στην εικόνα: a \u003d 2*r. Στη συνέχεια, βρίσκουμε την περιοχή της πλατείας που περιγράφεται κοντά στον κύκλο με μια δεδομένη ακτίνα σύμφωνα με τον τύπο S \u003d και σε τετράγωνο. Λύση:

• Ας υποθέσουμε ότι η ακτίνα είναι 7. Η πλευρά του τετραγώνου Α είναι 2*7 \u003d 14.
• S \u003d 14 σε τετράγωνο \u003d 196.

Εάν καταλαβαίνετε την ουσία της επίλυσης τέτοιων προβλημάτων, τότε μπορείτε να τα λύσετε γρήγορα και απλά. Ας δούμε μερικά ακόμη παραδείγματα.

Παραδείγματα επίλυσης προβλημάτων στο θέμα "Square Square"

Για να διορθώσετε το υλικό που καλύπτεται και να θυμηθείτε όλους τους τύπους, είναι απαραίτητο να λύσετε διάφορα παραδείγματα προβλημάτων στο θέμα της "τετραγωνικής περιοχής". Ξεκινάμε με μια απλή εργασία και προχωρούμε στην επίλυση πιο περίπλοκων:

Τώρα ξέρετε πώς να χρησιμοποιήσετε τον τύπο για το τετράγωνο της πλατείας, πράγμα που σημαίνει ότι μπορείτε να κάνετε οποιαδήποτε εργασία. Επιτυχία στη μελλοντική εκπαίδευση!

Βίντεο: Υπολογισμός τετραγωνικής περιοχής