Πώς να λύσετε κινήσεις για κίνηση; Ο τύπος εξάρτησης μεταξύ ταχύτητας, χρόνου και απόστασης. Εργασίες και λύσεις.
Περιεχόμενο
- Ο τύπος για την εξάρτηση του χρόνου, της ταχύτητας και της απόστασης στην 4η τάξη: Πώς είναι η ταχύτητα, ο χρόνος, η απόσταση;
- Πώς να βρείτε χρόνο, γνωρίζοντας ταχύτητα και απόσταση;
- Πώς να βρείτε ταχύτητα εάν είναι γνωστή η ώρα και η απόσταση;
- Πώς να βρείτε μια απόσταση εάν είναι γνωστή ο χρόνος και η ταχύτητα;
- Γράψτε της ταχύτητας του σώματος στο χρόνο: Φωτογραφία
- Πίνακας 4 Κατηγορία: Ταχύτητα, Χρόνος, απόσταση
- Παραδείγματα επίλυσης προβλημάτων για ταχύτητα, χρόνο, απόσταση για το βαθμό 4
- Βίντεο: Εργασίες κίνησης
Ο τύπος για την εξάρτηση του χρόνου, της ταχύτητας και της απόστασης στην 4η τάξη: Πώς είναι η ταχύτητα, ο χρόνος, η απόσταση;
Οι άνθρωποι, τα ζώα ή τα αυτοκίνητα μπορούν να κινηθούν με μια συγκεκριμένη ταχύτητα. Για ένα συγκεκριμένο χρονικό διάστημα, μπορούν να πάνε ένα συγκεκριμένο μονοπάτι. Για παράδειγμα: Σήμερα μπορείτε να φτάσετε στο σχολείο σας σε μισή ώρα. Πηγαίνετε σε μια συγκεκριμένη ταχύτητα και ξεπεράσετε 1000 μέτρα σε 30 λεπτά. Το μονοπάτι που ξεπερνά ορίζεται στα μαθηματικά με την επιστολή ΜΙΚΡΟ.. Η ταχύτητα υποδεικνύεται από την επιστολή v. Και ο χρόνος για τον οποίο αρνήθηκε το μονοπάτι υποδεικνύεται από την επιστολή Τ.
- Διαδρομή - ΜΙΚΡΟ.
- Ταχύτητα- V
- Χρόνος - Τ
Εάν καθυστερείτε στο σχολείο, μπορείτε να πάτε με τον ίδιο τρόπο σε 20 λεπτά, αυξάνοντας την ταχύτητά σας. Έτσι, η ίδια διαδρομή μπορεί να ταξιδέψει σε διαφορετικές χρονικές στιγμές και σε διαφορετικές ταχύτητες.
Πώς εξαρτάται ο χρόνος διέλευσης από την ταχύτητα;
Όσο μεγαλύτερη είναι η ταχύτητα, τόσο πιο γρήγορα θα γίνει η απόσταση. Και όσο χαμηλότερη είναι η ταχύτητα, όσο περισσότερο χρόνο πρέπει να περάσετε το μονοπάτι.

Πώς να βρείτε χρόνο, γνωρίζοντας ταχύτητα και απόσταση;
Προκειμένου να βρείτε το χρόνο που πρέπει να περάσετε το μονοπάτι, πρέπει να γνωρίζετε την απόσταση και την ταχύτητα. Εάν η απόσταση χωρίζεται σε ταχύτητα, θα μάθετε την ώρα. Ένα παράδειγμα μιας τέτοιας εργασίας:
Το έργο του λαγού. Ο λαγός έφυγε από τον λύκο με ταχύτητα 1 χιλιομέτρου ανά λεπτό. Έτρεξε στην τρύπα του 3 χιλιόμετρα. Για τι ώρα έφτασε ο λαγός σε μια τρύπα;

Πώς είναι εύκολο να λύσετε τα προβλήματα για την κίνηση, όπου πρέπει να βρείτε μια απόσταση, χρόνο ή ταχύτητα;
- Διαβάστε προσεκτικά την εργασία και καθορίστε τι είναι γνωστό από τις συνθήκες του προβλήματος.
- Γράψτε αυτά τα δεδομένα στο σχέδιο.
- Γράψτε επίσης τι είναι άγνωστο και τι πρέπει να βρεθεί
- Χρησιμοποιήστε τον τύπο για εργασίες σχετικά με την απόσταση, το χρόνο και την ταχύτητα
- Εισαγάγετε τα γνωστά δεδομένα στον τύπο και λύστε το πρόβλημα
Λύση για το πρόβλημα για τον λαγό και τον λύκο.
- Από τις συνθήκες του προβλήματος, διαπιστώνουμε ότι γνωρίζουμε την ταχύτητα και την απόσταση.
- Επίσης, από τις συνθήκες του προβλήματος, καθορίζουμε ότι πρέπει να βρούμε το χρόνο που ο λαγός πρέπει να φτάσει στην τρύπα.

Γράφουμε στο σχέδιο αυτών των δεδομένων για παράδειγμα:
Απόσταση από την οπή - 3 χιλιόμετρα
Hare Speed \u200b\u200b- 1 χιλιόμετρο σε 1 λεπτό
Ο χρόνος είναι άγνωστος
Τώρα γράφουμε το ίδιο με τα μαθηματικά σημάδια:
ΜΙΚΡΟ. - 3 χιλιόμετρα
V - 1 χλμ./Λεπτό
Τ — ?
Θυμάμαι και γράφουμε μια φόρμουλα για να βρούμε το χρόνο στο σημειωματάριο:
t \u003d S: V
Τώρα γράφουμε τη λύση του προβλήματος με αριθμούς:
t \u003d 3: 1 \u003d 3 λεπτά
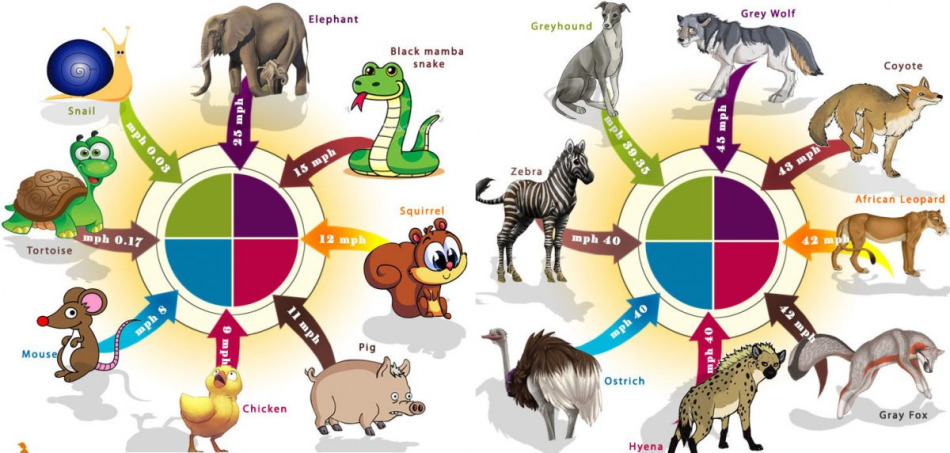
Πώς να βρείτε ταχύτητα εάν είναι γνωστή η ώρα και η απόσταση;
Προκειμένου να βρεθεί ταχύτητα, εάν είναι γνωστοί χρόνος και απόσταση, η απόσταση πρέπει να χωριστεί για λίγο. Ένα παράδειγμα μιας τέτοιας εργασίας:
Ο λαγός έφυγε από τον λύκο και έτρεξε στην τρύπα του 3 χιλιόμετρα. Έχει ξεπεράσει αυτή την απόσταση σε 3 λεπτά. Σε ποια ταχύτητα έτρεξε ο λαγός;
Επίλυση του προβλήματος της κίνησης:
- Στο σχέδιο, γράφουμε ότι γνωρίζουμε την απόσταση και το χρόνο.
- Από τις συνθήκες του προβλήματος, καθορίζουμε τι πρέπει να βρεθεί ταχύτητα
- Θυμηθείτε τη φόρμουλα για την εύρεση ταχύτητας.
Οι τύποι για την επίλυση τέτοιων προβλημάτων εμφανίζονται στην παρακάτω εικόνα.
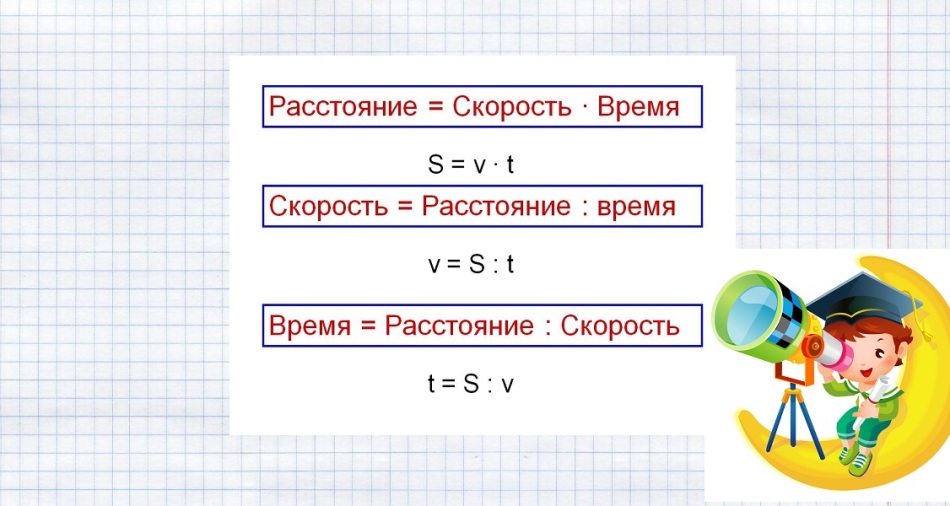
Αντικατοπτρίζουμε τα γνωστά δεδομένα και επιλύουμε το πρόβλημα:
Απόσταση από την οπή - 3 χιλιόμετρα
Ο χρόνος για τον οποίο ο λαγός έφτασε στην τρύπα είναι 3 λεπτά
Η ταχύτητα είναι άγνωστη
Γράφουμε αυτά τα γνωστά δεδομένα με μαθηματικά σημεία
ΜΙΚΡΟ. - 3 χιλιόμετρα
Τ - 3 λεπτά
v -?
Καταγράψτε τον τύπο για να βρείτε ταχύτητα
v \u003d s: t
Τώρα γράφουμε τη λύση του προβλήματος με αριθμούς:
v \u003d 3: 3 \u003d 1 χλμ./λεπτό

Πώς να βρείτε μια απόσταση εάν είναι γνωστή ο χρόνος και η ταχύτητα;
Για να βρείτε μια απόσταση, αν είναι γνωστή ώρα και ταχύτητα, είναι απαραίτητο να πολλαπλασιαστεί με ταχύτητα. Ένα παράδειγμα μιας τέτοιας εργασίας:
Ο λαγός έφυγε από τον λύκο με ταχύτητα 1 χιλιομέτρου σε 1 λεπτό. Τον χρειάστηκαν τρία λεπτά για να τρέξει στην τρύπα. Ποια απόσταση τρέχει ο λαγός;
Λύση του προβλήματος: Γράφουμε σε ένα σχέδιο που γνωρίζουμε από τις συνθήκες του προβλήματος:
Hare Speed \u200b\u200b- 1 χιλιόμετρο σε 1 λεπτό
Ο χρόνος που ο λαγός έφυγε στη Νόρα είναι 3 λεπτά
Η απόσταση είναι άγνωστη
Τώρα, θα γράψουμε το ίδιο πράγμα με τα μαθηματικά σημάδια:
v - 1 χλμ./Λεπτό
Τ - 3 λεπτά
S -?
Θυμηθείτε τη φόρμουλα για την εύρεση της απόστασης:
S \u003d v ⋅ t
Τώρα γράφουμε τη λύση του προβλήματος με αριθμούς:
S \u003d 3 ⋅ 1 \u003d 3 χλμ.

Πώς να μάθετε να λύσετε πιο περίπλοκα προβλήματα;
Για να μάθετε πώς να λύσετε πιο πολύπλοκα καθήκοντα, πρέπει να καταλάβετε πώς επιλύονται απλές εργασίες, θυμηθείτε ποια σημάδια υποδεικνύουν την απόσταση, την ταχύτητα και το χρόνο. Εάν δεν είναι δυνατόν να θυμηθούμε τους μαθηματικούς τύπους, πρέπει να γράφονται σε ένα φύλλο χαρτιού και να διατηρούνται πάντα στο χέρι κατά την επίλυση προβλημάτων. Λύστε με το παιδί σας απλές εργασίες που μπορούν να επινοηθούν εν κινήσει, για παράδειγμα, κατά τη διάρκεια μιας βόλτας.

Μονάδες
Όταν επιλύουν προβλήματα σχετικά με την ταχύτητα, το χρόνο και την απόσταση, συχνά κάνουν λάθος, λόγω του γεγονότος ότι ξέχασαν να μεταφράζουν μονάδες μέτρησης.
Σημαντικό: Οι μονάδες μέτρησης μπορούν να είναι οποιαδήποτε, αλλά αν υπάρχουν διαφορετικές μονάδες μετρήσεων σε μία εργασία, μεταφράστε τις το ίδιο. Για παράδειγμα, εάν η ταχύτητα μετριέται σε χιλιόμετρα ανά λεπτό, τότε η απόσταση πρέπει να παρουσιάζεται σε χιλιόμετρα και ο χρόνος σε λίγα λεπτά.
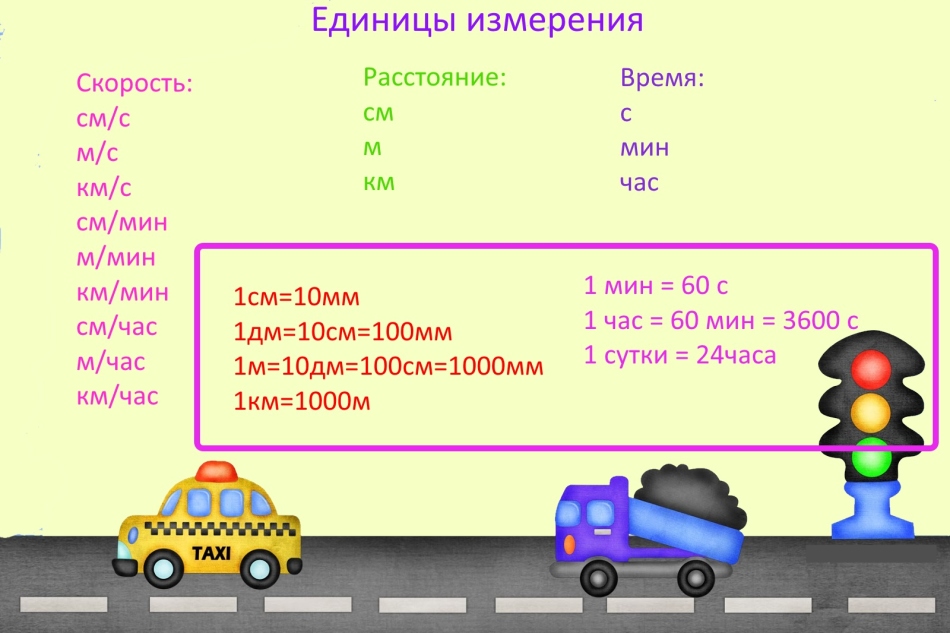
Για περίεργο: Το γενικά αποδεκτό σύστημα μέτρων ονομάζεται Metric τώρα, αλλά αυτό δεν συνέβαινε πάντα, και στις παλιές μέρες στις άλλες μονάδες διάστασης του Rus χρησιμοποιήθηκαν.

Το έργο του boas: Ο ελέφαντας και ο πίθηκος μέτρησαν το μήκος του συστημάτων BOA με βήματα. Κινήθηκαν ο ένας προς τον άλλον. Η ταχύτητα του πιθήκου ήταν 60 cm σε ένα δευτερόλεπτο και η ταχύτητα του ελέφαντα είναι 20 cm σε ένα δευτερόλεπτο. Πέρασαν 5 δευτερόλεπτα στη μέτρηση. Ποιο είναι το μήκος του συσσωματώματος BOA; (απόφαση κάτω από την εικόνα)

Λύση:
Από τις συνθήκες του προβλήματος, διαπιστώνουμε ότι γνωρίζουμε την ταχύτητα του πιθήκου και του ελέφαντα και του χρόνου που έπρεπε να μετρήσουν το μήκος της ώθησης.
Γράφουμε αυτά τα δεδομένα:
Ταχύτητα μαϊμού - 60 cm/s
Ταχύτητα ελέφαντα - 20 cm/s
Ώρα - 5 δευτερόλεπτα
Η απόσταση είναι άγνωστη
Γράφουμε αυτά τα δεδομένα με μαθηματικά σημάδια:
v1 - 60 cm/s
v2 - 20 cm/s
t - 5 δευτερόλεπτα
S -?
Ας γράψουμε τη φόρμουλα για την απόσταση εάν είναι γνωστοί η ταχύτητα και ο χρόνος:
S \u003d v ⋅ t
Υπολογίζουμε τον τρόπο με τον οποίο έχει περάσει η μαϊμού:
S1 \u003d 60 ⋅ 5 \u003d 300 cm
Τώρα ας υπολογίσουμε πόσο έχει περάσει ο ελέφαντας:
S2 \u003d 20 ⋅ 5 \u003d 100 cm
Συνοψίζουμε την απόσταση που πέρασε ο πίθηκος και η απόσταση που πέρασε ο ελέφαντας:
S \u003d S1 + S2 \u003d 300 + 100 \u003d 400 cm
Γράψτε της ταχύτητας του σώματος στο χρόνο: Φωτογραφία
Η απόσταση που ξεπερνά με διαφορετικές ταχύτητες ξεπερνά σε διαφορετικούς χρόνους. Όσο μεγαλύτερη είναι η ταχύτητα, τόσο λιγότερο χρόνο θα πάρει.
Πίνακας 4 Κατηγορία: Ταχύτητα, Χρόνος, απόσταση
Ο παρακάτω πίνακας δείχνει τα δεδομένα για τα οποία πρέπει να βρείτε προβλήματα και στη συνέχεια να τα λύσετε.
| № | Ταχύτητα (km/Ώρα) | Ώρα (ώρα) | Απόσταση (χλμ.) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Μπορείτε να φανταστείτε και να βρείτε καθήκοντα για το τραπέζι μόνοι σας. Παρακάτω είναι οι επιλογές μας για εργασίες:
- Η μαμά έστειλε ένα κόκκινο καπέλο στη γιαγιά της. Το κορίτσι ήταν συνεχώς αποσπασματικό και περπάτησε αργά μέσα στο δάσος, με ταχύτητα 5 χλμ./H. Πέρασε 2 ώρες στο μονοπάτι. Ποια απόσταση έχει περάσει ένα κόκκινο καπάκι κατά τη διάρκεια αυτής της περιόδου;
- Το Postman Pechkin παίρνει ένα δέμα σε ποδήλατο με ταχύτητα 12 χλμ./H. Ξέρει ότι η απόσταση μεταξύ του σπιτιού του και του σπιτιού του θείου Fedor είναι 12 χλμ. Βοήθεια Pechkin Υπολογίστε πόσο καιρό θα χρειαστεί για το δρόμο;
- Ο μπαμπάς Ksyusha αγόρασε ένα αυτοκίνητο και αποφάσισε να πάρει την οικογένειά του στη θάλασσα. Το αυτοκίνητο οδηγούσε με ταχύτητα 60 χλμ./Ώρα και 4 ώρες δαπανήθηκαν στο δρόμο. Ποια είναι η απόσταση μεταξύ του σπιτιού του Ksyusha και της ακτής της θάλασσας;
- Οι πάπιες συγκεντρώθηκαν στη σφήνα και πέταξαν στις ζεστές άκρες. Τα πουλιά έτρεξαν τα φτερά τους κουρασμένα για 3 ώρες και ξεπέρασαν 300 χλμ. Κατά τη διάρκεια αυτής της περιόδου. Ποια ήταν η ταχύτητα των πτηνών;
- Το αεροσκάφος AN-2 πετάει με ταχύτητα 220 km/h. Πέταξε από τη Μόσχα και πετάει στο Nizhny Novgorod, η απόσταση μεταξύ αυτών των δύο πόλεων είναι 440 χλμ. Πόσο καιρό θα ακολουθήσει το αεροπλάνο;

Οι απαντήσεις στις παραπάνω εργασίες μπορούν να βρεθούν στον παρακάτω πίνακα:
| № | Ταχύτητα (km/Ώρα) | Ώρα (ώρα) | Απόσταση (χλμ.) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Παραδείγματα επίλυσης προβλημάτων για ταχύτητα, χρόνο, απόσταση για το βαθμό 4
Εάν υπάρχουν πολλά αντικείμενα κίνησης σε μια εργασία, πρέπει να διδάξετε στο παιδί να εξετάσει την κίνηση αυτών των αντικειμένων ξεχωριστά και μόνο τότε μαζί. Ένα παράδειγμα μιας τέτοιας εργασίας:
Δύο φίλοι του Vadik και το θέμα αποφάσισαν να κάνουν μια βόλτα και να εγκαταλείψουν τα σπίτια τους ο ένας προς τον άλλον. Ο Vadik οδήγησε ένα ποδήλατο και το θέμα περπατούσε. Ο Vadik οδήγησε με ταχύτητα 10 χλμ./H, και το θέμα ήταν σε ταχύτητα 5 χλμ. Ανά ώρα. Μια ώρα αργότερα συναντήθηκαν. Ποια είναι η απόσταση μεταξύ των σπιτιών και των θεμάτων του Vadik;
Αυτό το πρόβλημα μπορεί να λυθεί χρησιμοποιώντας τον τύπο για την εξάρτηση της απόστασης από την ταχύτητα και το χρόνο.
S \u003d v ⋅ t
Η απόσταση που ο Vadik οδήγησε σε ποδήλατο θα είναι ίση με την ταχύτητά του πολλαπλασιασμένη με το ταξίδι.
S \u003d 10 ⋅ 1 \u003d 10 χιλιόμετρα
Η απόσταση που έχει περάσει το θέμα θεωρείται ομοίως:
S \u003d v ⋅ t
Αντικατοπτρίζουμε τις ψηφιακές τιμές της ταχύτητας και του χρόνου του στον τύπο
S \u003d 5 ⋅ 1 \u003d 5 χιλιόμετρα
Η απόσταση που οδήγησε ο Vadik πρέπει να προστεθεί στην απόσταση που πέρασε το θέμα.
10 + 5 \u003d 15 χιλιόμετρα
Πώς να μάθετε πώς να λύσετε σύνθετα προβλήματα, για την επίλυση που πρέπει να σκεφτείτε λογικά;
Για να αναπτύξετε τη λογική σκέψη του παιδιού, πρέπει να λύσετε μαζί του απλή και στη συνέχεια σύνθετα λογικά προβλήματα. Αυτά τα καθήκοντα μπορεί να αποτελούνται από διάφορα στάδια. Είναι δυνατόν να μετακινηθείτε μόνο από το ένα στάδιο σε άλλο εάν επιλυθεί το προηγούμενο. Ένα παράδειγμα μιας τέτοιας εργασίας:
Ο Anton πήγε σε ποδήλατο με ταχύτητα 12 χλμ./Ώρα και η Λίζα οδήγησε σε ένα σκούτερ με ταχύτητα 2 φορές μικρότερη από εκείνη του Αντόνου και ο Ντένις περπάτησε με ταχύτητα 2 φορές μικρότερη από αυτή της Λίζας. Ποια είναι η ταχύτητα του Denis;
Για να λύσετε αυτό το πρόβλημα, πρέπει πρώτα να μάθετε την ταχύτητα της Λίζα και μόνο μετά από αυτή την ταχύτητα του Denis.

Μερικές φορές στα εγχειρίδια για 4 βαθμούς υπάρχουν δύσκολες εργασίες. Ένα παράδειγμα μιας τέτοιας εργασίας:
Δύο ποδηλάτες άφησαν διαφορετικές πόλεις ο ένας προς τον άλλον. Ένας από αυτούς έσπευσε και αγωνίστηκε με ταχύτητα 12 χλμ./H, και ο δεύτερος οδήγησε αργά με ταχύτητα 8 km/h. Η απόσταση μεταξύ των πόλεων από τις οποίες οι ποδηλάτες έφυγαν από 60 χλμ. Ποια απόσταση θα περάσει κάθε ποδηλάτης, πριν συναντηθούν; (απόφαση κάτω από τη φωτογραφία)

Λύση:
- 12+8 \u003d 20 (km/h) είναι η συνολική ταχύτητα δύο ποδηλάτων ή η ταχύτητα με την οποία πλησίασαν ο ένας τον άλλον
- 60 : 20 \u003d 3 (ώρες) - Αυτός είναι ο χρόνος μέσω του οποίου συναντήθηκαν οι ποδηλάτες
- 3 ⋅ 8 \u003d 24 (χλμ.) Είναι η απόσταση που οδήγησε ο πρώτος ποδηλάτης
- 12 ⋅ 3\u003d 36 (km) είναι η απόσταση που οδήγησε ο δεύτερος ποδηλάτης
- Έλεγχος: 36+24 \u003d 60 (km) είναι η απόσταση που ταξίδεψαν δύο ποδηλάτες.
- Απάντηση: 24 χλμ., 36 χλμ.
Προσφέρετε στα παιδιά με τη μορφή ενός παιχνιδιού για την επίλυση τέτοιων προβλημάτων. Ίσως οι ίδιοι θα θέλουν να συνθέσουν το έργο τους για φίλους, ζώα ή πουλιά.







